Provably Efficient Multi-Objective Bandit Algorithms under Preference-Centric Customization
Paper and Code
Feb 19, 2025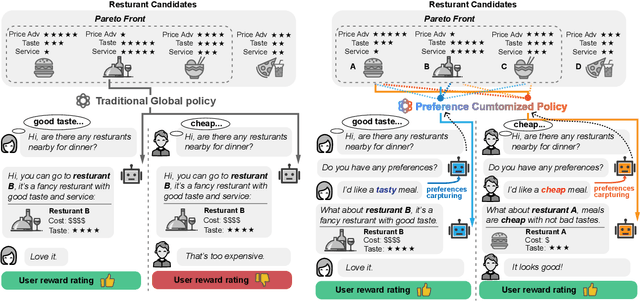
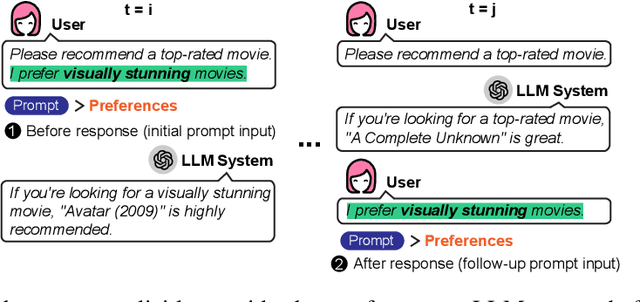
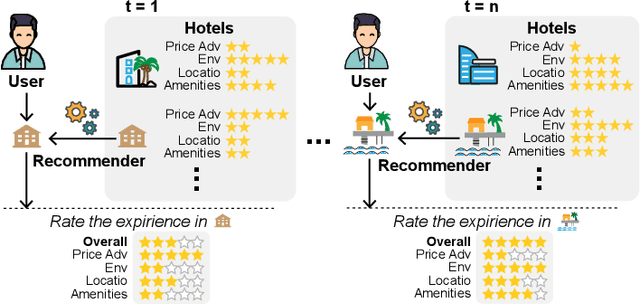
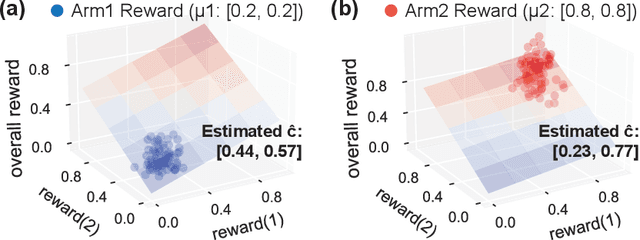
Multi-objective multi-armed bandit (MO-MAB) problems traditionally aim to achieve Pareto optimality. However, real-world scenarios often involve users with varying preferences across objectives, resulting in a Pareto-optimal arm that may score high for one user but perform quite poorly for another. This highlights the need for customized learning, a factor often overlooked in prior research. To address this, we study a preference-aware MO-MAB framework in the presence of explicit user preference. It shifts the focus from achieving Pareto optimality to further optimizing within the Pareto front under preference-centric customization. To our knowledge, this is the first theoretical study of customized MO-MAB optimization with explicit user preferences. Motivated by practical applications, we explore two scenarios: unknown preference and hidden preference, each presenting unique challenges for algorithm design and analysis. At the core of our algorithms are preference estimation and preference-aware optimization mechanisms to adapt to user preferences effectively. We further develop novel analytical techniques to establish near-optimal regret of the proposed algorithms. Strong empirical performance confirm the effectiveness of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge