How to Find the Exact Pareto Front for Multi-Objective MDPs?

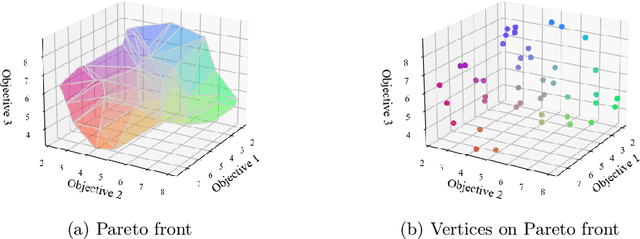
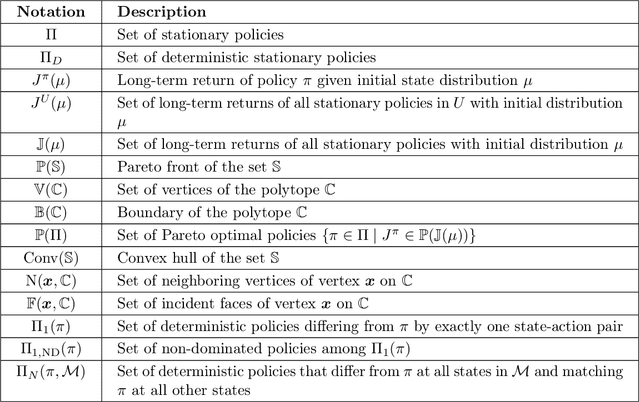
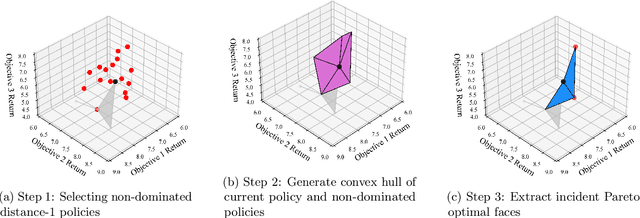
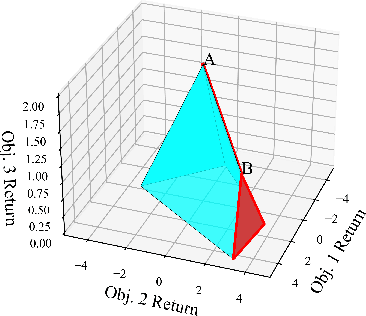
Multi-objective Markov Decision Processes (MDPs) are receiving increasing attention, as real-world decision-making problems often involve conflicting objectives that cannot be addressed by a single-objective MDP. The Pareto front identifies the set of policies that cannot be dominated, providing a foundation for finding optimal solutions that can efficiently adapt to various preferences. However, finding the Pareto front is a highly challenging problem. Most existing methods either (i) rely on traversing the continuous preference space, which is impractical and results in approximations that are difficult to evaluate against the true Pareto front, or (ii) focus solely on deterministic Pareto optimal policies, from which there are no known techniques to characterize the full Pareto front. Moreover, finding the structure of the Pareto front itself remains unclear even in the context of dynamic programming. This work addresses the challenge of efficiently discovering the Pareto front. By investigating the geometric structure of the Pareto front in MO-MDP, we uncover a key property: the Pareto front is on the boundary of a convex polytope whose vertices all correspond to deterministic policies, and neighboring vertices of the Pareto front differ by only one state-action pair of the deterministic policy, almost surely. This insight transforms the global comparison across all policies into a localized search among deterministic policies that differ by only one state-action pair, drastically reducing the complexity of searching for the exact Pareto front. We develop an efficient algorithm that identifies the vertices of the Pareto front by solving a single-objective MDP only once and then traversing the edges of the Pareto front, making it more efficient than existing methods. Our empirical studies demonstrate the effectiveness of our theoretical strategy in discovering the Pareto front.