Peizhong Ju
Evaluating Sparse Autoencoders for Monosemantic Representation
Aug 20, 2025Abstract:A key barrier to interpreting large language models is polysemanticity, where neurons activate for multiple unrelated concepts. Sparse autoencoders (SAEs) have been proposed to mitigate this issue by transforming dense activations into sparse, more interpretable features. While prior work suggests that SAEs promote monosemanticity, there has been no quantitative comparison with their base models. This paper provides the first systematic evaluation of SAEs against base models concerning monosemanticity. We introduce a fine-grained concept separability score based on the Jensen-Shannon distance, which captures how distinctly a neuron's activation distributions vary across concepts. Using Gemma-2-2B and multiple SAE variants across five benchmarks, we show that SAEs reduce polysemanticity and achieve higher concept separability. However, greater sparsity of SAEs does not always yield better separability and often impairs downstream performance. To assess practical utility, we evaluate concept-level interventions using two strategies: full neuron masking and partial suppression. We find that, compared to base models, SAEs enable more precise concept-level control when using partial suppression. Building on this, we propose Attenuation via Posterior Probabilities (APP), a new intervention method that uses concept-conditioned activation distributions for targeted suppression. APP outperforms existing approaches in targeted concept removal.
FSL-SAGE: Accelerating Federated Split Learning via Smashed Activation Gradient Estimation
May 29, 2025Abstract:Collaborative training methods like Federated Learning (FL) and Split Learning (SL) enable distributed machine learning without sharing raw data. However, FL assumes clients can train entire models, which is infeasible for large-scale models. In contrast, while SL alleviates the client memory constraint in FL by offloading most training to the server, it increases network latency due to its sequential nature. Other methods address the conundrum by using local loss functions for parallel client-side training to improve efficiency, but they lack server feedback and potentially suffer poor accuracy. We propose FSL-SAGE (Federated Split Learning via Smashed Activation Gradient Estimation), a new federated split learning algorithm that estimates server-side gradient feedback via auxiliary models. These auxiliary models periodically adapt to emulate server behavior on local datasets. We show that FSL-SAGE achieves a convergence rate of $\mathcal{O}(1/\sqrt{T})$, where $T$ is the number of communication rounds. This result matches FedAvg, while significantly reducing communication costs and client memory requirements. Our empirical results also verify that it outperforms existing state-of-the-art FSL methods, offering both communication efficiency and accuracy.
BeST -- A Novel Source Selection Metric for Transfer Learning
Jan 19, 2025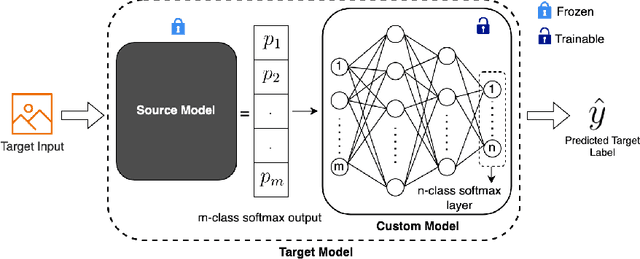

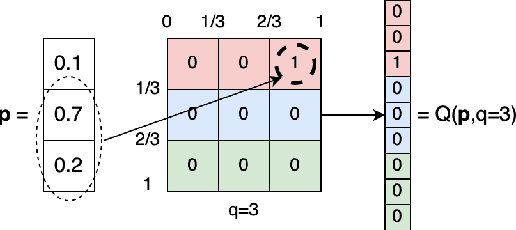

Abstract:One of the most fundamental, and yet relatively less explored, goals in transfer learning is the efficient means of selecting top candidates from a large number of previously trained models (optimized for various "source" tasks) that would perform the best for a new "target" task with a limited amount of data. In this paper, we undertake this goal by developing a novel task-similarity metric (BeST) and an associated method that consistently performs well in identifying the most transferrable source(s) for a given task. In particular, our design employs an innovative quantization-level optimization procedure in the context of classification tasks that yields a measure of similarity between a source model and the given target data. The procedure uses a concept similar to early stopping (usually implemented to train deep neural networks (DNNs) to ensure generalization) to derive a function that approximates the transfer learning mapping without training. The advantage of our metric is that it can be quickly computed to identify the top candidate(s) for a given target task before a computationally intensive transfer operation (typically using DNNs) can be implemented between the selected source and the target task. As such, our metric can provide significant computational savings for transfer learning from a selection of a large number of possible source models. Through extensive experimental evaluations, we establish that our metric performs well over different datasets and varying numbers of data samples.
PSMGD: Periodic Stochastic Multi-Gradient Descent for Fast Multi-Objective Optimization
Dec 17, 2024Abstract:Multi-objective optimization (MOO) lies at the core of many machine learning (ML) applications that involve multiple, potentially conflicting objectives (e.g., multi-task learning, multi-objective reinforcement learning, among many others). Despite the long history of MOO, recent years have witnessed a surge in interest within the ML community in the development of gradient manipulation algorithms for MOO, thanks to the availability of gradient information in many ML problems. However, existing gradient manipulation methods for MOO often suffer from long training times, primarily due to the need for computing dynamic weights by solving an additional optimization problem to determine a common descent direction that can decrease all objectives simultaneously. To address this challenge, we propose a new and efficient algorithm called Periodic Stochastic Multi-Gradient Descent (PSMGD) to accelerate MOO. PSMGD is motivated by the key observation that dynamic weights across objectives exhibit small changes under minor updates over short intervals during the optimization process. Consequently, our PSMGD algorithm is designed to periodically compute these dynamic weights and utilizes them repeatedly, thereby effectively reducing the computational overload. Theoretically, we prove that PSMGD can achieve state-of-the-art convergence rates for strongly-convex, general convex, and non-convex functions. Additionally, we introduce a new computational complexity measure, termed backpropagation complexity, and demonstrate that PSMGD could achieve an objective-independent backpropagation complexity. Through extensive experiments, we verify that PSMGD can provide comparable or superior performance to state-of-the-art MOO algorithms while significantly reducing training time.
How to Find the Exact Pareto Front for Multi-Objective MDPs?
Oct 21, 2024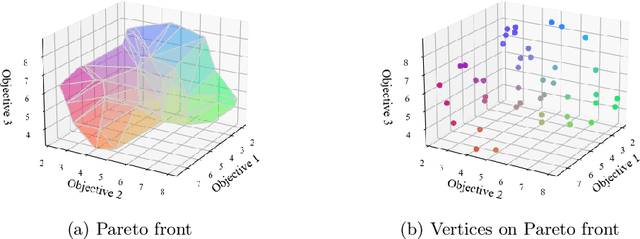
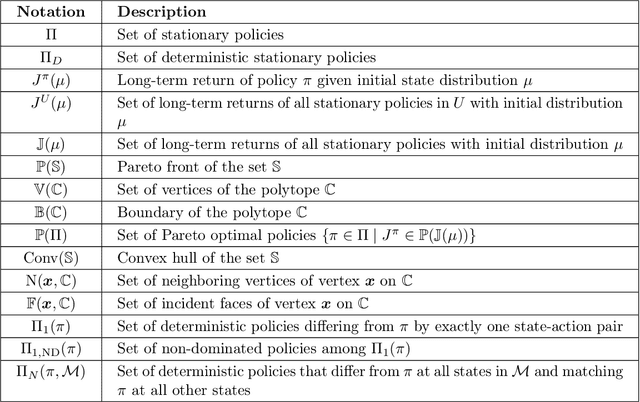
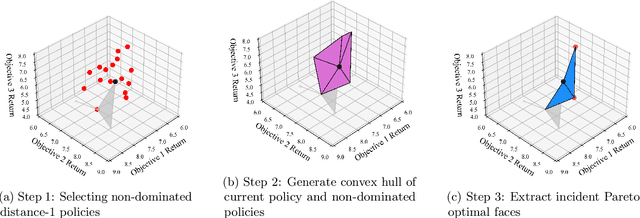
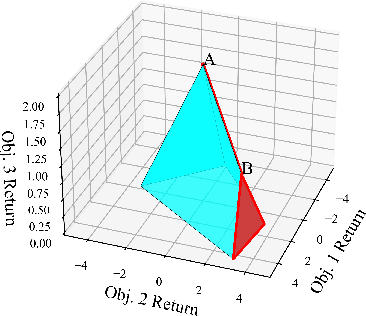
Abstract:Multi-objective Markov Decision Processes (MDPs) are receiving increasing attention, as real-world decision-making problems often involve conflicting objectives that cannot be addressed by a single-objective MDP. The Pareto front identifies the set of policies that cannot be dominated, providing a foundation for finding optimal solutions that can efficiently adapt to various preferences. However, finding the Pareto front is a highly challenging problem. Most existing methods either (i) rely on traversing the continuous preference space, which is impractical and results in approximations that are difficult to evaluate against the true Pareto front, or (ii) focus solely on deterministic Pareto optimal policies, from which there are no known techniques to characterize the full Pareto front. Moreover, finding the structure of the Pareto front itself remains unclear even in the context of dynamic programming. This work addresses the challenge of efficiently discovering the Pareto front. By investigating the geometric structure of the Pareto front in MO-MDP, we uncover a key property: the Pareto front is on the boundary of a convex polytope whose vertices all correspond to deterministic policies, and neighboring vertices of the Pareto front differ by only one state-action pair of the deterministic policy, almost surely. This insight transforms the global comparison across all policies into a localized search among deterministic policies that differ by only one state-action pair, drastically reducing the complexity of searching for the exact Pareto front. We develop an efficient algorithm that identifies the vertices of the Pareto front by solving a single-objective MDP only once and then traversing the edges of the Pareto front, making it more efficient than existing methods. Our empirical studies demonstrate the effectiveness of our theoretical strategy in discovering the Pareto front.
Theory on Score-Mismatched Diffusion Models and Zero-Shot Conditional Samplers
Oct 17, 2024

Abstract:The denoising diffusion model has recently emerged as a powerful generative technique, capable of transforming noise into meaningful data. While theoretical convergence guarantees for diffusion models are well established when the target distribution aligns with the training distribution, practical scenarios often present mismatches. One common case is in zero-shot conditional diffusion sampling, where the target conditional distribution is different from the (unconditional) training distribution. These score-mismatched diffusion models remain largely unexplored from a theoretical perspective. In this paper, we present the first performance guarantee with explicit dimensional dependencies for general score-mismatched diffusion samplers, focusing on target distributions with finite second moments. We show that score mismatches result in an asymptotic distributional bias between the target and sampling distributions, proportional to the accumulated mismatch between the target and training distributions. This result can be directly applied to zero-shot conditional samplers for any conditional model, irrespective of measurement noise. Interestingly, the derived convergence upper bound offers useful guidance for designing a novel bias-optimal zero-shot sampler in linear conditional models that minimizes the asymptotic bias. For such bias-optimal samplers, we further establish convergence guarantees with explicit dependencies on dimension and conditioning, applied to several interesting target distributions, including those with bounded support and Gaussian mixtures. Our findings are supported by numerical studies.
Can We Theoretically Quantify the Impacts of Local Updates on the Generalization Performance of Federated Learning?
Sep 05, 2024



Abstract:Federated Learning (FL) has gained significant popularity due to its effectiveness in training machine learning models across diverse sites without requiring direct data sharing. While various algorithms along with their optimization analyses have shown that FL with local updates is a communication-efficient distributed learning framework, the generalization performance of FL with local updates has received comparatively less attention. This lack of investigation can be attributed to the complex interplay between data heterogeneity and infrequent communication due to the local updates within the FL framework. This motivates us to investigate a fundamental question in FL: Can we quantify the impact of data heterogeneity and local updates on the generalization performance for FL as the learning process evolves? To this end, we conduct a comprehensive theoretical study of FL's generalization performance using a linear model as the first step, where the data heterogeneity is considered for both the stationary and online/non-stationary cases. By providing closed-form expressions of the model error, we rigorously quantify the impact of the number of the local updates (denoted as $K$) under three settings ($K=1$, $K<\infty$, and $K=\infty$) and show how the generalization performance evolves with the number of rounds $t$. Our investigation also provides a comprehensive understanding of how different configurations (including the number of model parameters $p$ and the number of training samples $n$) contribute to the overall generalization performance, thus shedding new insights (such as benign overfitting) for implementing FL over networks.
Non-asymptotic Convergence of Discrete-time Diffusion Models: New Approach and Improved Rate
Feb 21, 2024

Abstract:The denoising diffusion model emerges recently as a powerful generative technique that converts noise into data. Theoretical convergence guarantee has been mainly studied for continuous-time diffusion models, and has been obtained for discrete-time diffusion models only for distributions with bounded support in the literature. In this paper, we establish the convergence guarantee for substantially larger classes of distributions under discrete-time diffusion models and further improve the convergence rate for distributions with bounded support. In particular, we first establish the convergence rates for both smooth and general (possibly non-smooth) distributions having finite second moment. We then specialize our results to a number of interesting classes of distributions with explicit parameter dependencies, including distributions with Lipschitz scores, Gaussian mixture distributions, and distributions with bounded support. We further propose a novel accelerated sampler and show that it improves the convergence rates of the corresponding regular sampler by orders of magnitude with respect to all system parameters. For distributions with bounded support, our result improves the dimensional dependence of the previous convergence rate by orders of magnitude. Our study features a novel analysis technique that constructs tilting factor representation of the convergence error and exploits Tweedie's formula for handling Taylor expansion power terms.
Achieving Sample and Computational Efficient Reinforcement Learning by Action Space Reduction via Grouping
Jun 22, 2023

Abstract:Reinforcement learning often needs to deal with the exponential growth of states and actions when exploring optimal control in high-dimensional spaces (often known as the curse of dimensionality). In this work, we address this issue by learning the inherent structure of action-wise similar MDP to appropriately balance the performance degradation versus sample/computational complexity. In particular, we partition the action spaces into multiple groups based on the similarity in transition distribution and reward function, and build a linear decomposition model to capture the difference between the intra-group transition kernel and the intra-group rewards. Both our theoretical analysis and experiments reveal a \emph{surprising and counter-intuitive result}: while a more refined grouping strategy can reduce the approximation error caused by treating actions in the same group as identical, it also leads to increased estimation error when the size of samples or the computation resources is limited. This finding highlights the grouping strategy as a new degree of freedom that can be optimized to minimize the overall performance loss. To address this issue, we formulate a general optimization problem for determining the optimal grouping strategy, which strikes a balance between performance loss and sample/computational complexity. We further propose a computationally efficient method for selecting a nearly-optimal grouping strategy, which maintains its computational complexity independent of the size of the action space.
Generalization Performance of Transfer Learning: Overparameterized and Underparameterized Regimes
Jun 09, 2023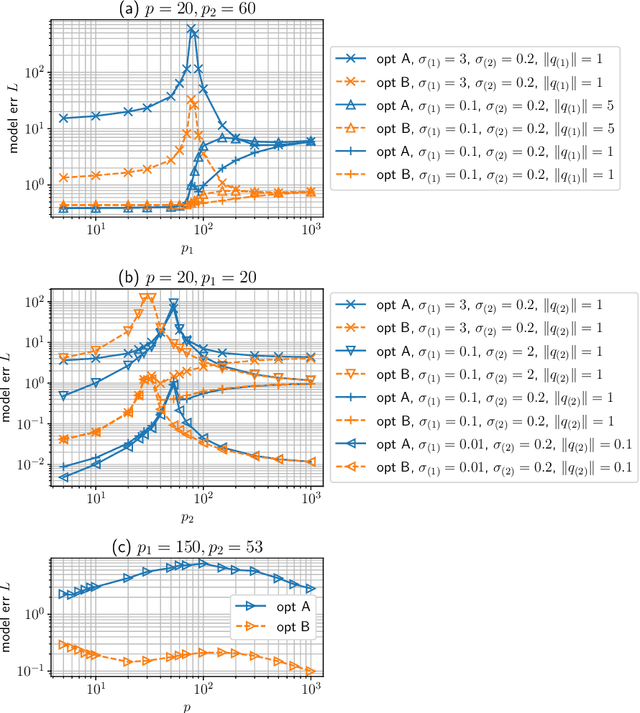
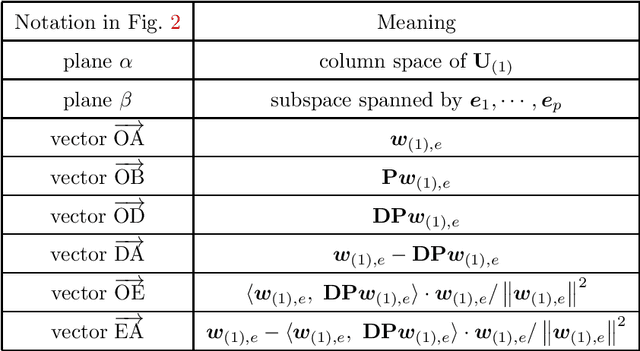
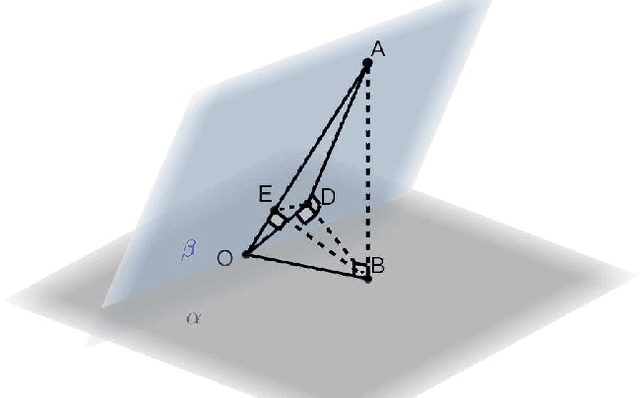
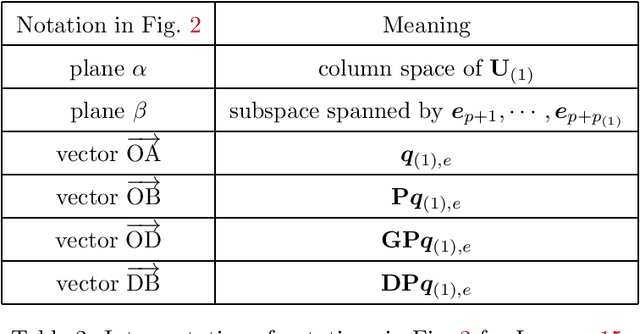
Abstract:Transfer learning is a useful technique for achieving improved performance and reducing training costs by leveraging the knowledge gained from source tasks and applying it to target tasks. Assessing the effectiveness of transfer learning relies on understanding the similarity between the ground truth of the source and target tasks. In real-world applications, tasks often exhibit partial similarity, where certain aspects are similar while others are different or irrelevant. To investigate the impact of partial similarity on transfer learning performance, we focus on a linear regression model with two distinct sets of features: a common part shared across tasks and a task-specific part. Our study explores various types of transfer learning, encompassing two options for parameter transfer. By establishing a theoretical characterization on the error of the learned model, we compare these transfer learning options, particularly examining how generalization performance changes with the number of features/parameters in both underparameterized and overparameterized regimes. Furthermore, we provide practical guidelines for determining the number of features in the common and task-specific parts for improved generalization performance. For example, when the total number of features in the source task's learning model is fixed, we show that it is more advantageous to allocate a greater number of redundant features to the task-specific part rather than the common part. Moreover, in specific scenarios, particularly those characterized by high noise levels and small true parameters, sacrificing certain true features in the common part in favor of employing more redundant features in the task-specific part can yield notable benefits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge