Theory on Score-Mismatched Diffusion Models and Zero-Shot Conditional Samplers

The denoising diffusion model has recently emerged as a powerful generative technique, capable of transforming noise into meaningful data. While theoretical convergence guarantees for diffusion models are well established when the target distribution aligns with the training distribution, practical scenarios often present mismatches. One common case is in zero-shot conditional diffusion sampling, where the target conditional distribution is different from the (unconditional) training distribution. These score-mismatched diffusion models remain largely unexplored from a theoretical perspective. In this paper, we present the first performance guarantee with explicit dimensional dependencies for general score-mismatched diffusion samplers, focusing on target distributions with finite second moments. We show that score mismatches result in an asymptotic distributional bias between the target and sampling distributions, proportional to the accumulated mismatch between the target and training distributions. This result can be directly applied to zero-shot conditional samplers for any conditional model, irrespective of measurement noise. Interestingly, the derived convergence upper bound offers useful guidance for designing a novel bias-optimal zero-shot sampler in linear conditional models that minimizes the asymptotic bias. For such bias-optimal samplers, we further establish convergence guarantees with explicit dependencies on dimension and conditioning, applied to several interesting target distributions, including those with bounded support and Gaussian mixtures. Our findings are supported by numerical studies.

Learning Quantized Adaptive Conditions for Diffusion Models

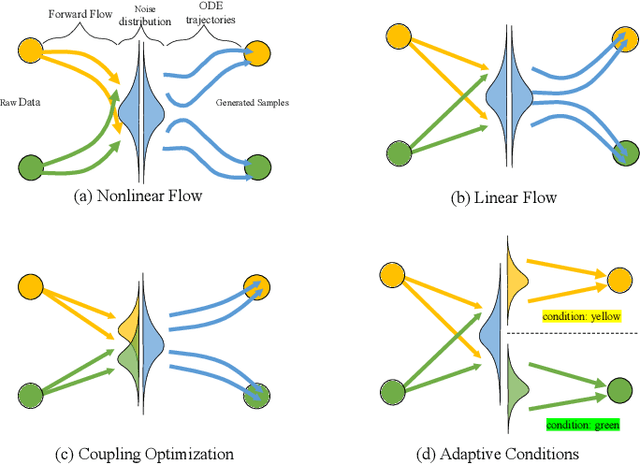
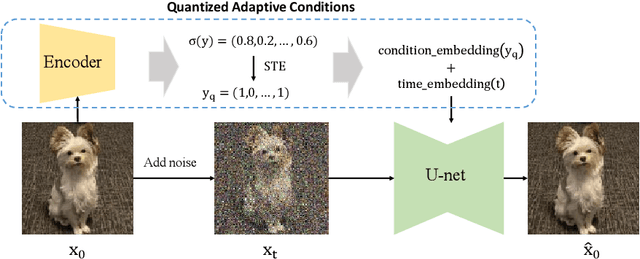
The curvature of ODE trajectories in diffusion models hinders their ability to generate high-quality images in a few number of function evaluations (NFE). In this paper, we propose a novel and effective approach to reduce trajectory curvature by utilizing adaptive conditions. By employing a extremely light-weight quantized encoder, our method incurs only an additional 1% of training parameters, eliminates the need for extra regularization terms, yet achieves significantly better sample quality. Our approach accelerates ODE sampling while preserving the downstream task image editing capabilities of SDE techniques. Extensive experiments verify that our method can generate high quality results under extremely limited sampling costs. With only 6 NFE, we achieve 5.14 FID on CIFAR-10, 6.91 FID on FFHQ 64x64 and 3.10 FID on AFHQv2.

Non-asymptotic Convergence of Discrete-time Diffusion Models: New Approach and Improved Rate

The denoising diffusion model emerges recently as a powerful generative technique that converts noise into data. Theoretical convergence guarantee has been mainly studied for continuous-time diffusion models, and has been obtained for discrete-time diffusion models only for distributions with bounded support in the literature. In this paper, we establish the convergence guarantee for substantially larger classes of distributions under discrete-time diffusion models and further improve the convergence rate for distributions with bounded support. In particular, we first establish the convergence rates for both smooth and general (possibly non-smooth) distributions having finite second moment. We then specialize our results to a number of interesting classes of distributions with explicit parameter dependencies, including distributions with Lipschitz scores, Gaussian mixture distributions, and distributions with bounded support. We further propose a novel accelerated sampler and show that it improves the convergence rates of the corresponding regular sampler by orders of magnitude with respect to all system parameters. For distributions with bounded support, our result improves the dimensional dependence of the previous convergence rate by orders of magnitude. Our study features a novel analysis technique that constructs tilting factor representation of the convergence error and exploits Tweedie's formula for handling Taylor expansion power terms.

Less is More: Physical-enhanced Radar-Inertial Odometry

Radar offers the advantage of providing additional physical properties related to observed objects. In this study, we design a physical-enhanced radar-inertial odometry system that capitalizes on the Doppler velocities and radar cross-section information. The filter for static radar points, correspondence estimation, and residual functions are all strengthened by integrating the physical properties. We conduct experiments on both public datasets and our self-collected data, with different mobile platforms and sensor types. Our quantitative results demonstrate that the proposed radar-inertial odometry system outperforms alternative methods using the physical-enhanced components. Our findings also reveal that using the physical properties results in fewer radar points for odometry estimation, but the performance is still guaranteed and even improved, thus aligning with the ``less is more'' principle.

Quickest Change Detection with Post-Change Density Estimation

The problem of quickest change detection in a sequence of independent observations is considered. The pre-change distribution is assumed to be known, while the post-change distribution is unknown. Two tests based on post-change density estimation are developed for this problem, the window-limited non-parametric generalized likelihood ratio (NGLR) CuSum test and the non-parametric window-limited adaptive (NWLA) CuSum test. Both tests do not assume any knowledge of the post-change distribution, except that the post-change density satisfies certain smoothness conditions that allows for efficient non-parametric estimation. Also, they do not require any pre-collected post-change training samples. Under certain convergence conditions on the density estimator, it is shown that both tests are first-order asymptotically optimal, as the false alarm rate goes to zero. The analysis is validated through numerical results, where both tests are compared with baseline tests that have distributional knowledge.

Energy Transformer

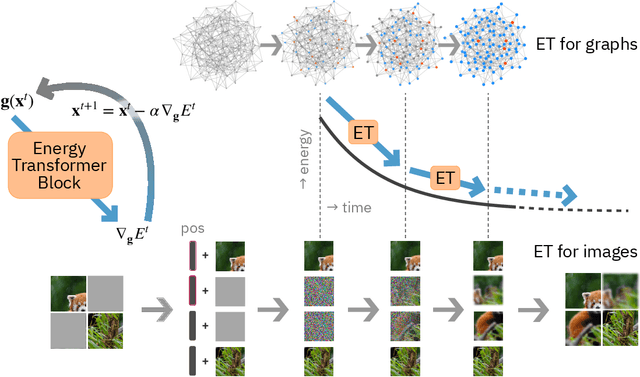
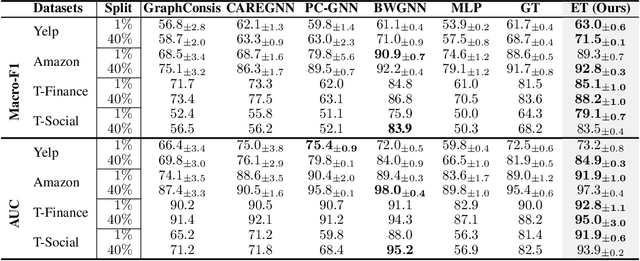
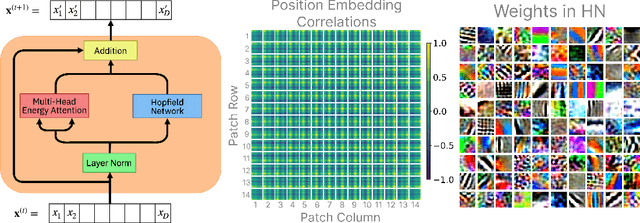
Transformers have become the de facto models of choice in machine learning, typically leading to impressive performance on many applications. At the same time, the architectural development in the transformer world is mostly driven by empirical findings, and the theoretical understanding of their architectural building blocks is rather limited. In contrast, Dense Associative Memory models or Modern Hopfield Networks have a well-established theoretical foundation, but have not yet demonstrated truly impressive practical results. We propose a transformer architecture that replaces the sequence of feedforward transformer blocks with a single large Associative Memory model. Our novel architecture, called Energy Transformer (or ET for short), has many of the familiar architectural primitives that are often used in the current generation of transformers. However, it is not identical to the existing architectures. The sequence of transformer layers in ET is purposely designed to minimize a specifically engineered energy function, which is responsible for representing the relationships between the tokens. As a consequence of this computational principle, the attention in ET is different from the conventional attention mechanism. In this work, we introduce the theoretical foundations of ET, explore it's empirical capabilities using the image completion task, and obtain strong quantitative results on the graph anomaly detection task.

Quickest Change Detection with Leave-one-out Density Estimation

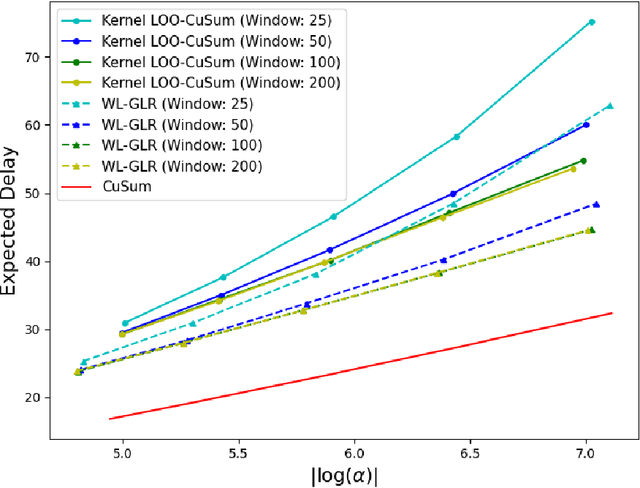
The problem of quickest change detection in a sequence of independent observations is considered. The pre-change distribution is assumed to be known, while the post-change distribution is completely unknown. A window-limited leave-one-out (LOO) CuSum test is developed, which does not assume any knowledge of the post-change distribution, and does not require any post-change training samples. It is shown that, with certain convergence conditions on the density estimator, the LOO-CuSum test is first-order asymptotically optimal, as the false alarm rate goes to zero. The analysis is validated through numerical results, where the LOO-CuSum test is compared with baseline tests that have distributional knowledge.

Associative Learning for Network Embedding

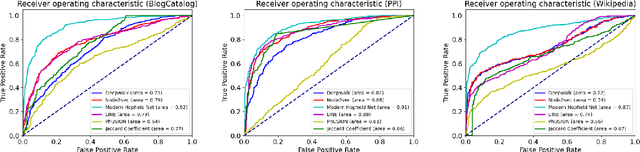
The network embedding task is to represent the node in the network as a low-dimensional vector while incorporating the topological and structural information. Most existing approaches solve this problem by factorizing a proximity matrix, either directly or implicitly. In this work, we introduce a network embedding method from a new perspective, which leverages Modern Hopfield Networks (MHN) for associative learning. Our network learns associations between the content of each node and that node's neighbors. These associations serve as memories in the MHN. The recurrent dynamics of the network make it possible to recover the masked node, given that node's neighbors. Our proposed method is evaluated on different downstream tasks such as node classification and linkage prediction. The results show competitive performance compared to the common matrix factorization techniques and deep learning based methods.

Keyphrase Extraction Using Neighborhood Knowledge Based on Word Embeddings

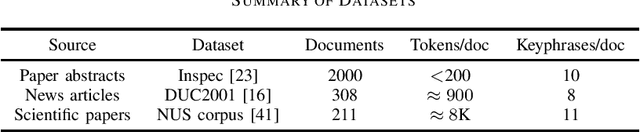
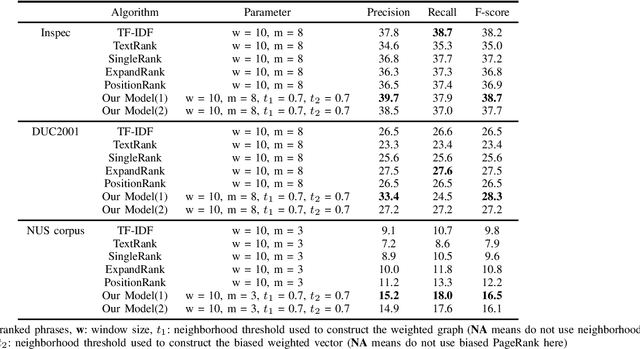
Keyphrase extraction is the task of finding several interesting phrases in a text document, which provide a list of the main topics within the document. Most existing graph-based models use co-occurrence links as cohesion indicators to model the relationship of syntactic elements. However, a word may have different forms of expression within the document, and may have several synonyms as well. Simply using co-occurrence information cannot capture this information. In this paper, we enhance the graph-based ranking model by leveraging word embeddings as background knowledge to add semantic information to the inter-word graph. Our approach is evaluated on established benchmark datasets and empirical results show that the word embedding neighborhood information improves the model performance.

Quickest Change Detection with Non-stationary and Composite Post-change Distribution

The problem of quickest detection of a change in the distribution of a sequence of independent observations is considered. The pre-change distribution is assumed to be known and stationary, while the post-change distributions are assumed to evolve in a pre-determined non-stationary manner with some possible parametric uncertainty. In particular, it is assumed that the cumulative KL divergence between the post-change and the pre-change distributions grows super-linearly with time after the change-point. For the case where the post-change distributions are known, a universal asymptotic lower bound on the delay is derived, as the false alarm rate goes to zero. Furthermore, a window-limited CuSum test is developed, and shown to achieve the lower bound asymptotically. For the case where the post-change distributions have parametric uncertainty, a window-limited generalized likelihood-ratio test is developed and is shown to achieve the universal lower bound asymptotically. Extensions to the case with dependent observations are discussed. The analysis is validated through numerical results on synthetic data. The use of the window-limited generalized likelihood-ratio test in monitoring pandemics is also demonstrated.