Quickest Change Detection with Leave-one-out Density Estimation
Paper and Code
Nov 04, 2022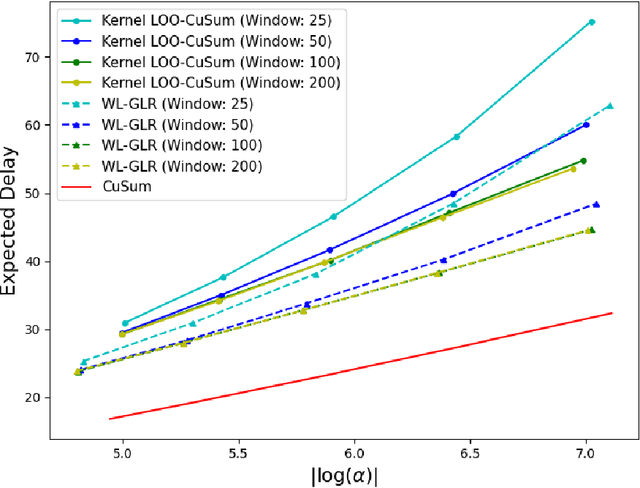
The problem of quickest change detection in a sequence of independent observations is considered. The pre-change distribution is assumed to be known, while the post-change distribution is completely unknown. A window-limited leave-one-out (LOO) CuSum test is developed, which does not assume any knowledge of the post-change distribution, and does not require any post-change training samples. It is shown that, with certain convergence conditions on the density estimator, the LOO-CuSum test is first-order asymptotically optimal, as the false alarm rate goes to zero. The analysis is validated through numerical results, where the LOO-CuSum test is compared with baseline tests that have distributional knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge