Venugopal V. Veeravalli
Finite-Horizon Quickest Change Detection Balancing Latency with False Alarm Probability
Nov 16, 2025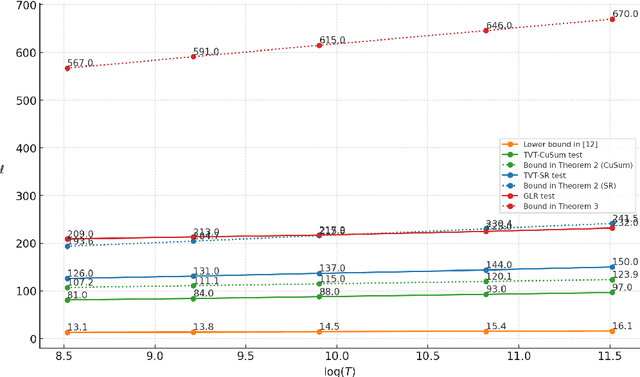
Abstract:A finite-horizon variant of the quickest change detection (QCD) problem that is of relevance to learning in non-stationary environments is studied. The metric characterizing false alarms is the probability of a false alarm occurring before the horizon ends. The metric that characterizes the delay is \emph{latency}, which is the smallest value such that the probability that detection delay exceeds this value is upper bounded to a predetermined latency level. The objective is to minimize the latency (at a given latency level), while maintaining a low false alarm probability. Under the pre-specified latency and false alarm levels, a universal lower bound on the latency, which any change detection procedure needs to satisfy, is derived. Change detectors are then developed, which are order-optimal in terms of the horizon. The case where the pre- and post-change distributions are known is considered first, and then the results are generalized to the non-parametric case when they are unknown except that they are sub-Gaussian with different means. Simulations are provided to validate the theoretical results.
Detection Is All You Need: A Feasible Optimal Prior-Free Black-Box Approach For Piecewise Stationary Bandits
Jan 31, 2025



Abstract:We study the problem of piecewise stationary bandits without prior knowledge of the underlying non-stationarity. We propose the first $\textit{feasible}$ black-box algorithm applicable to most common parametric bandit variants. Our procedure, termed Detection Augmented Bandit (DAB), is modular, accepting any stationary bandit algorithm as input and augmenting it with a change detector. DAB achieves optimal regret in the piecewise stationary setting under mild assumptions. Specifically, we prove that DAB attains the order-optimal regret bound of $\tilde{\mathcal{O}}(\sqrt{N_T T})$, where $N_T$ denotes the number of changes over the horizon $T$, if its input stationary bandit algorithm has order-optimal stationary regret guarantees. Applying DAB to different parametric bandit settings, we recover recent state-of-the-art results. Notably, for self-concordant bandits, DAB achieves optimal dynamic regret, while previous works obtain suboptimal bounds and require knowledge on the non-stationarity. In simulations on piecewise stationary environments, DAB outperforms existing approaches across varying number of changes. Interestingly, despite being theoretically designed for piecewise stationary environments, DAB is also effective in simulations in drifting environments, outperforming existing methods designed specifically for this scenario.
Change Detection-Based Procedures for Piecewise Stationary MABs: A Modular Approach
Jan 02, 2025
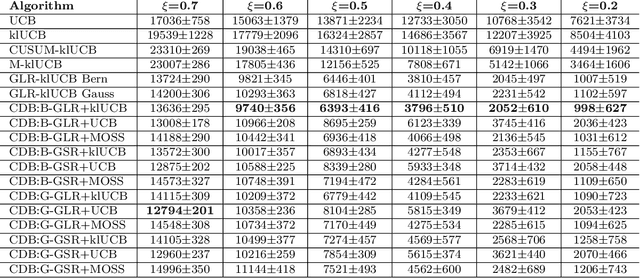
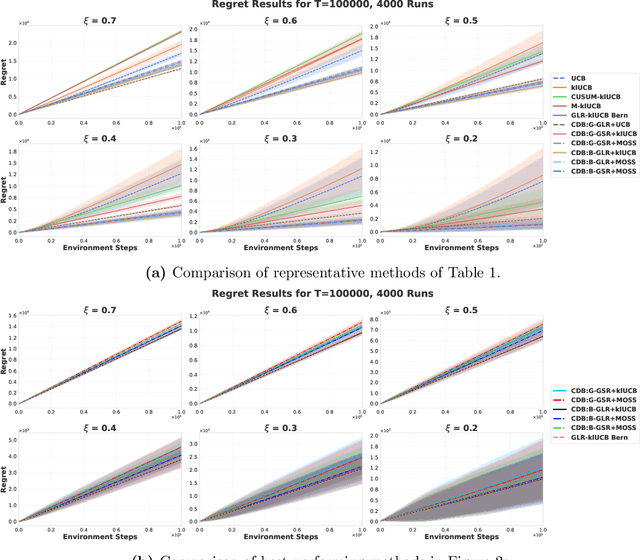
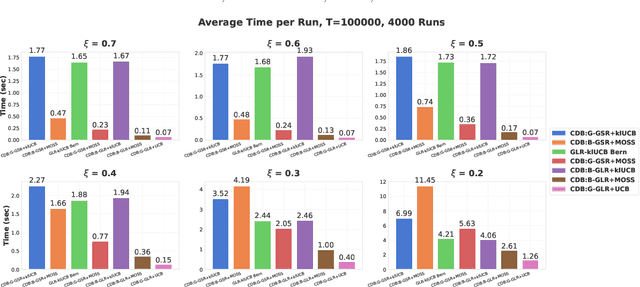
Abstract:Conventional Multi-Armed Bandit (MAB) algorithms are designed for stationary environments, where the reward distributions associated with the arms do not change with time. In many applications, however, the environment is more accurately modeled as being nonstationary. In this work, piecewise stationary MAB (PS-MAB) environments are investigated, in which the reward distributions associated with a subset of the arms change at some change-points and remain stationary between change-points. Our focus is on the asymptotic analysis of PS-MABs, for which practical algorithms based on change detection (CD) have been previously proposed. Our goal is to modularize the design and analysis of such CD-based Bandit (CDB) procedures. To this end, we identify the requirements for stationary bandit algorithms and change detectors in a CDB procedure that are needed for the modularization. We assume that the rewards are sub-Gaussian. Under this assumption and a condition on the separation of the change-points, we show that the analysis of CDB procedures can indeed be modularized, so that regret bounds can be obtained in a unified manner for various combinations of change detectors and bandit algorithms. Through this analysis, we develop new modular CDB procedures that are order-optimal. We compare the performance of our modular CDB procedures with various other methods in simulations.
Is Prior-Free Black-Box Non-Stationary Reinforcement Learning Feasible?
Oct 17, 2024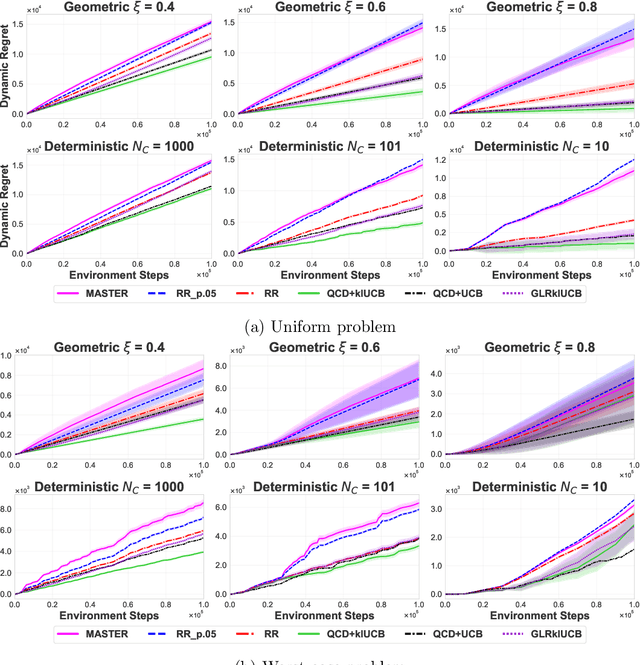
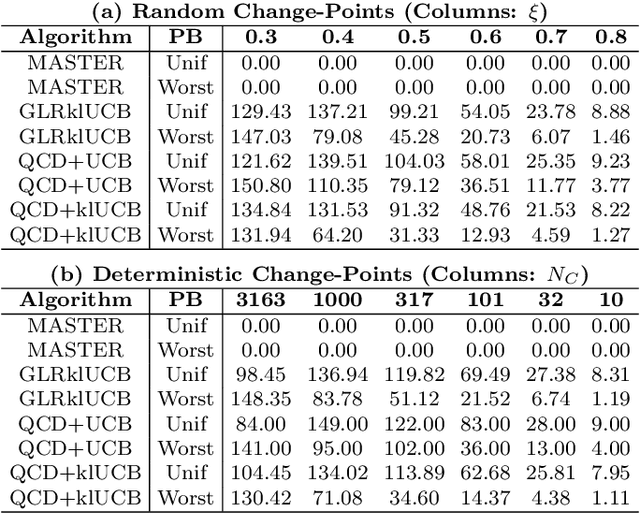
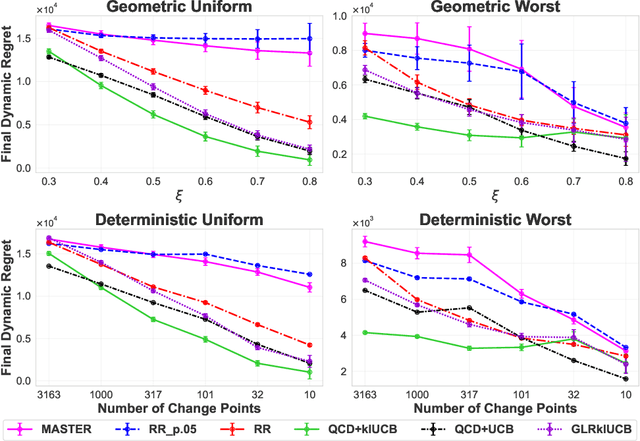
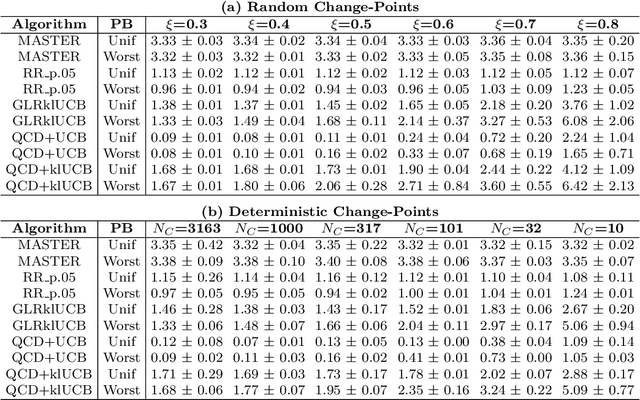
Abstract:We study the problem of Non-Stationary Reinforcement Learning (NS-RL) without prior knowledge about the system's non-stationarity. A state-of-the-art, black-box algorithm, known as MASTER, is considered, with a focus on identifying the conditions under which it can achieve its stated goals. Specifically, we prove that MASTER's non-stationarity detection mechanism is not triggered for practical choices of horizon, leading to performance akin to a random restarting algorithm. Moreover, we show that the regret bound for MASTER, while being order optimal, stays above the worst-case linear regret until unreasonably large values of the horizon. To validate these observations, MASTER is tested for the special case of piecewise stationary multi-armed bandits, along with methods that employ random restarting, and others that use quickest change detection to restart. A simple, order optimal random restarting algorithm, that has prior knowledge of the non-stationarity is proposed as a baseline. The behavior of the MASTER algorithm is validated in simulations, and it is shown that methods employing quickest change detection are more robust and consistently outperform MASTER and other random restarting approaches.
Track-MDP: Reinforcement Learning for Target Tracking with Controlled Sensing
Jul 19, 2024Abstract:State of the art methods for target tracking with sensor management (or controlled sensing) are model-based and are obtained through solutions to Partially Observable Markov Decision Process (POMDP) formulations. In this paper a Reinforcement Learning (RL) approach to the problem is explored for the setting where the motion model for the object/target to be tracked is unknown to the observer. It is assumed that the target dynamics are stationary in time, the state space and the observation space are discrete, and there is complete observability of the location of the target under certain (a priori unknown) sensor control actions. Then, a novel Markov Decision Process (MDP) rather than POMDP formulation is proposed for the tracking problem with controlled sensing, which is termed as Track-MDP. In contrast to the POMDP formulation, the Track-MDP formulation is amenable to an RL based solution. It is shown that the optimal policy for the Track-MDP formulation, which is approximated through RL, is guaranteed to track all significant target paths with certainty. The Track-MDP method is then compared with the optimal POMDP policy, and it is shown that the infinite horizon tracking reward of the optimal Track-MDP policy is the same as that of the optimal POMDP policy. In simulations it is demonstrated that Track-MDP based RL leads to a policy that can track the target with high accuracy.
Quickest Change Detection with Confusing Change
May 01, 2024Abstract:In the problem of quickest change detection (QCD), a change occurs at some unknown time in the distribution of a sequence of independent observations. This work studies a QCD problem where the change is either a bad change, which we aim to detect, or a confusing change, which is not of our interest. Our objective is to detect a bad change as quickly as possible while avoiding raising a false alarm for pre-change or a confusing change. We identify a specific set of pre-change, bad change, and confusing change distributions that pose challenges beyond the capabilities of standard Cumulative Sum (CuSum) procedures. Proposing novel CuSum-based detection procedures, S-CuSum and J-CuSum, leveraging two CuSum statistics, we offer solutions applicable across all kinds of pre-change, bad change, and confusing change distributions. For both S-CuSum and J-CuSum, we provide analytical performance guarantees and validate them by numerical results. Furthermore, both procedures are computationally efficient as they only require simple recursive updates.
Distributed and Rate-Adaptive Feature Compression
Apr 02, 2024



Abstract:We study the problem of distributed and rate-adaptive feature compression for linear regression. A set of distributed sensors collect disjoint features of regressor data. A fusion center is assumed to contain a pretrained linear regression model, trained on a dataset of the entire uncompressed data. At inference time, the sensors compress their observations and send them to the fusion center through communication-constrained channels, whose rates can change with time. Our goal is to design a feature compression {scheme} that can adapt to the varying communication constraints, while maximizing the inference performance at the fusion center. We first obtain the form of optimal quantizers assuming knowledge of underlying regressor data distribution. Under a practically reasonable approximation, we then propose a distributed compression scheme which works by quantizing a one-dimensional projection of the sensor data. We also propose a simple adaptive scheme for handling changes in communication constraints. We demonstrate the effectiveness of the distributed adaptive compression scheme through simulated experiments.
Quickest Change Detection with Post-Change Density Estimation
Nov 25, 2023



Abstract:The problem of quickest change detection in a sequence of independent observations is considered. The pre-change distribution is assumed to be known, while the post-change distribution is unknown. Two tests based on post-change density estimation are developed for this problem, the window-limited non-parametric generalized likelihood ratio (NGLR) CuSum test and the non-parametric window-limited adaptive (NWLA) CuSum test. Both tests do not assume any knowledge of the post-change distribution, except that the post-change density satisfies certain smoothness conditions that allows for efficient non-parametric estimation. Also, they do not require any pre-collected post-change training samples. Under certain convergence conditions on the density estimator, it is shown that both tests are first-order asymptotically optimal, as the false alarm rate goes to zero. The analysis is validated through numerical results, where both tests are compared with baseline tests that have distributional knowledge.
Quickest Change Detection with Leave-one-out Density Estimation
Nov 04, 2022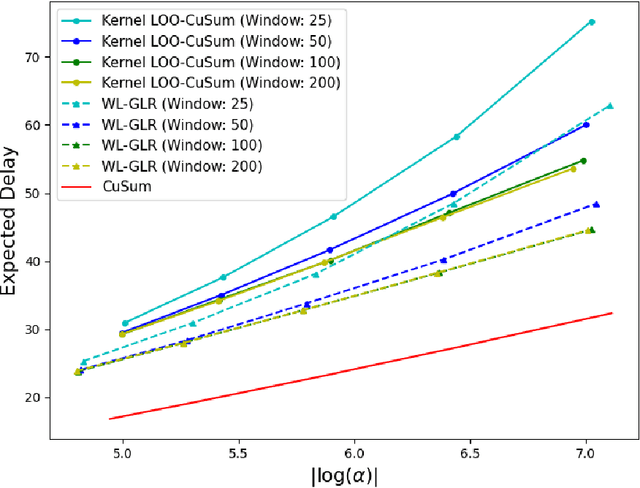
Abstract:The problem of quickest change detection in a sequence of independent observations is considered. The pre-change distribution is assumed to be known, while the post-change distribution is completely unknown. A window-limited leave-one-out (LOO) CuSum test is developed, which does not assume any knowledge of the post-change distribution, and does not require any post-change training samples. It is shown that, with certain convergence conditions on the density estimator, the LOO-CuSum test is first-order asymptotically optimal, as the false alarm rate goes to zero. The analysis is validated through numerical results, where the LOO-CuSum test is compared with baseline tests that have distributional knowledge.
Adaptive Step-Size Methods for Compressed SGD
Jul 20, 2022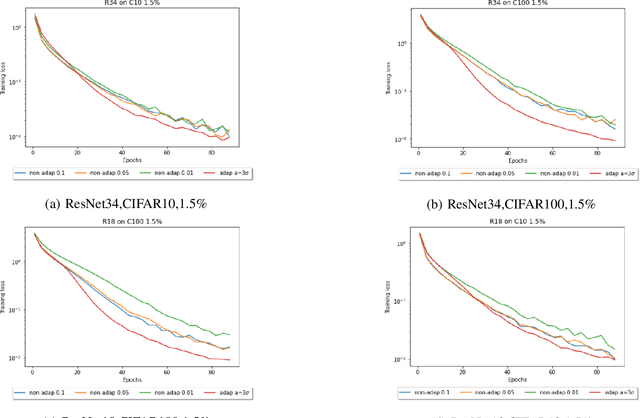
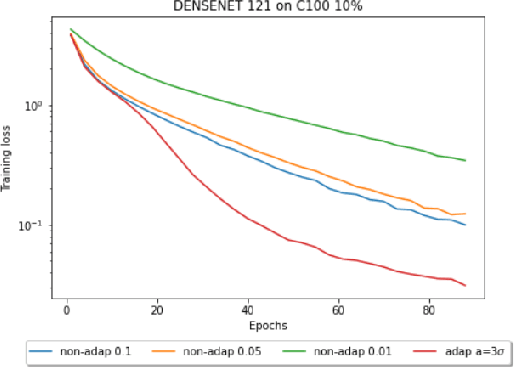
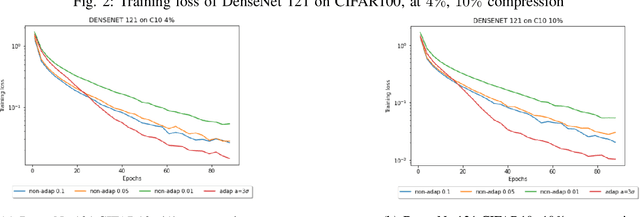
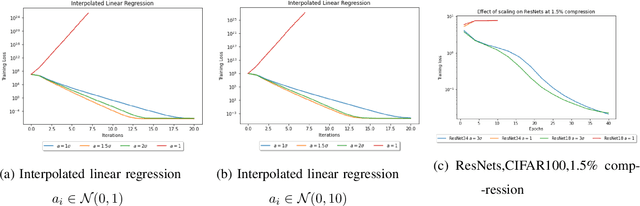
Abstract:Compressed Stochastic Gradient Descent (SGD) algorithms have been recently proposed to address the communication bottleneck in distributed and decentralized optimization problems, such as those that arise in federated machine learning. Existing compressed SGD algorithms assume the use of non-adaptive step-sizes(constant or diminishing) to provide theoretical convergence guarantees. Typically, the step-sizes are fine-tuned in practice to the dataset and the learning algorithm to provide good empirical performance. Such fine-tuning might be impractical in many learning scenarios, and it is therefore of interest to study compressed SGD using adaptive step-sizes. Motivated by prior work on adaptive step-size methods for SGD to train neural networks efficiently in the uncompressed setting, we develop an adaptive step-size method for compressed SGD. In particular, we introduce a scaling technique for the descent step in compressed SGD, which we use to establish order-optimal convergence rates for convex-smooth and strong convex-smooth objectives under an interpolation condition and for non-convex objectives under a strong growth condition. We also show through simulation examples that without this scaling, the algorithm can fail to converge. We present experimental results on deep neural networks for real-world datasets, and compare the performance of our proposed algorithm with previously proposed compressed SGD methods in literature, and demonstrate improved performance on ResNet-18, ResNet-34 and DenseNet architectures for CIFAR-100 and CIFAR-10 datasets at various levels of compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge