Detection Is All You Need: A Feasible Optimal Prior-Free Black-Box Approach For Piecewise Stationary Bandits

We study the problem of piecewise stationary bandits without prior knowledge of the underlying non-stationarity. We propose the first $\textit{feasible}$ black-box algorithm applicable to most common parametric bandit variants. Our procedure, termed Detection Augmented Bandit (DAB), is modular, accepting any stationary bandit algorithm as input and augmenting it with a change detector. DAB achieves optimal regret in the piecewise stationary setting under mild assumptions. Specifically, we prove that DAB attains the order-optimal regret bound of $\tilde{\mathcal{O}}(\sqrt{N_T T})$, where $N_T$ denotes the number of changes over the horizon $T$, if its input stationary bandit algorithm has order-optimal stationary regret guarantees. Applying DAB to different parametric bandit settings, we recover recent state-of-the-art results. Notably, for self-concordant bandits, DAB achieves optimal dynamic regret, while previous works obtain suboptimal bounds and require knowledge on the non-stationarity. In simulations on piecewise stationary environments, DAB outperforms existing approaches across varying number of changes. Interestingly, despite being theoretically designed for piecewise stationary environments, DAB is also effective in simulations in drifting environments, outperforming existing methods designed specifically for this scenario.

Change Detection-Based Procedures for Piecewise Stationary MABs: A Modular Approach

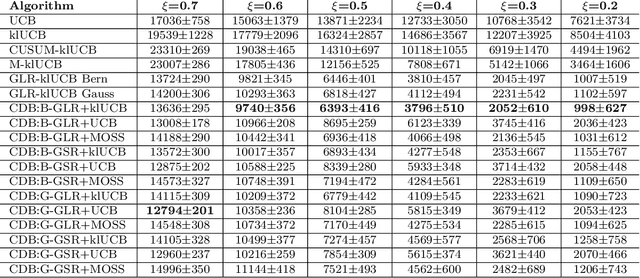
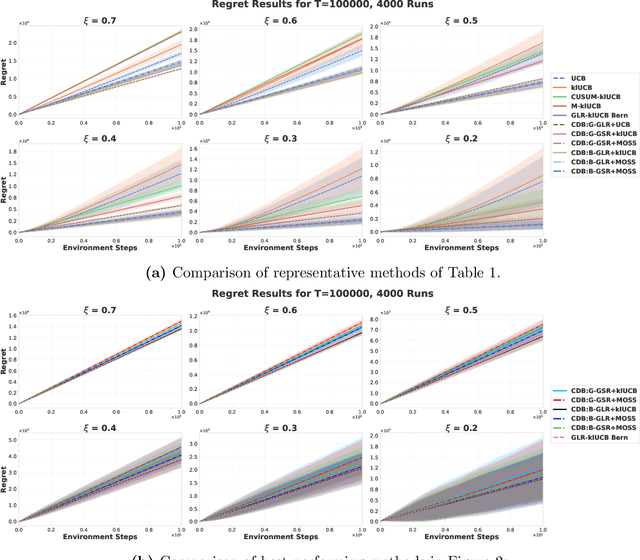
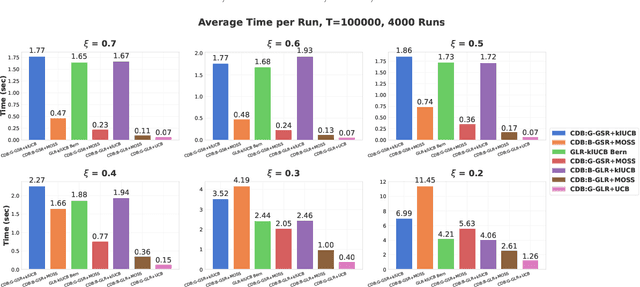
Conventional Multi-Armed Bandit (MAB) algorithms are designed for stationary environments, where the reward distributions associated with the arms do not change with time. In many applications, however, the environment is more accurately modeled as being nonstationary. In this work, piecewise stationary MAB (PS-MAB) environments are investigated, in which the reward distributions associated with a subset of the arms change at some change-points and remain stationary between change-points. Our focus is on the asymptotic analysis of PS-MABs, for which practical algorithms based on change detection (CD) have been previously proposed. Our goal is to modularize the design and analysis of such CD-based Bandit (CDB) procedures. To this end, we identify the requirements for stationary bandit algorithms and change detectors in a CDB procedure that are needed for the modularization. We assume that the rewards are sub-Gaussian. Under this assumption and a condition on the separation of the change-points, we show that the analysis of CDB procedures can indeed be modularized, so that regret bounds can be obtained in a unified manner for various combinations of change detectors and bandit algorithms. Through this analysis, we develop new modular CDB procedures that are order-optimal. We compare the performance of our modular CDB procedures with various other methods in simulations.

Is Prior-Free Black-Box Non-Stationary Reinforcement Learning Feasible?

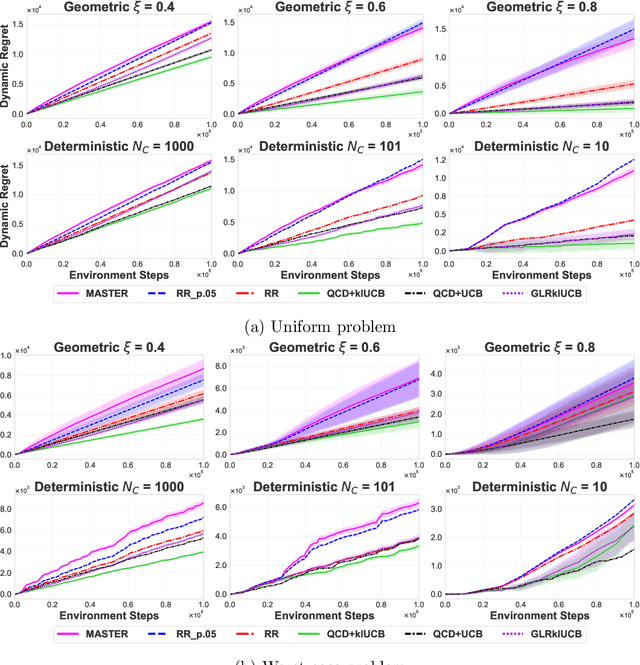
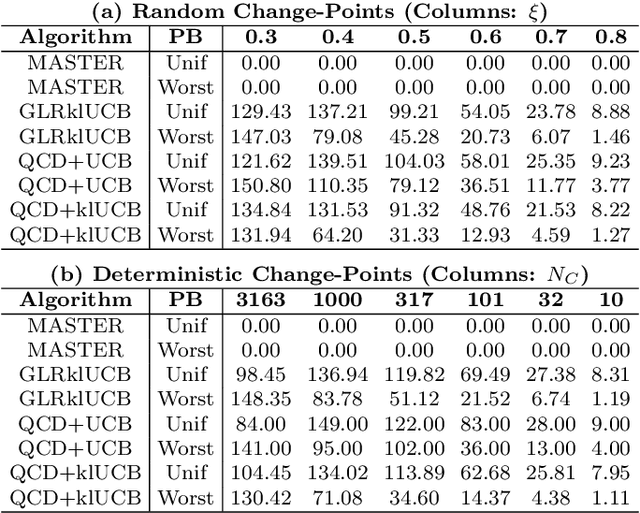
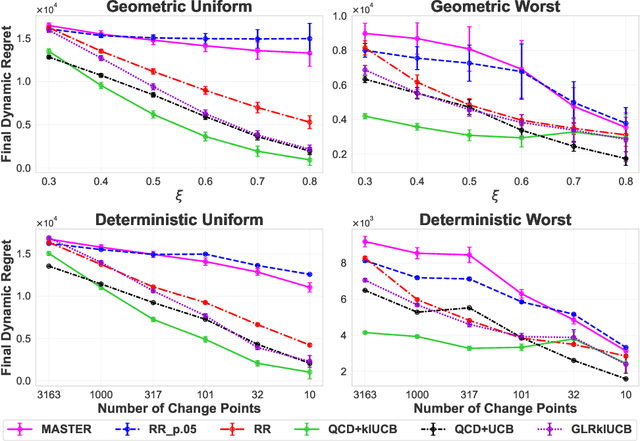
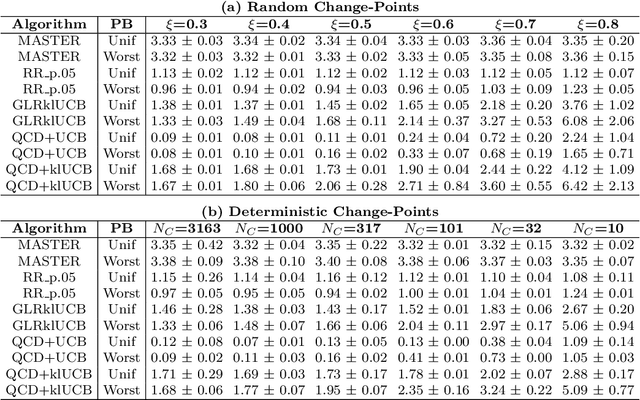
We study the problem of Non-Stationary Reinforcement Learning (NS-RL) without prior knowledge about the system's non-stationarity. A state-of-the-art, black-box algorithm, known as MASTER, is considered, with a focus on identifying the conditions under which it can achieve its stated goals. Specifically, we prove that MASTER's non-stationarity detection mechanism is not triggered for practical choices of horizon, leading to performance akin to a random restarting algorithm. Moreover, we show that the regret bound for MASTER, while being order optimal, stays above the worst-case linear regret until unreasonably large values of the horizon. To validate these observations, MASTER is tested for the special case of piecewise stationary multi-armed bandits, along with methods that employ random restarting, and others that use quickest change detection to restart. A simple, order optimal random restarting algorithm, that has prior knowledge of the non-stationarity is proposed as a baseline. The behavior of the MASTER algorithm is validated in simulations, and it is shown that methods employing quickest change detection are more robust and consistently outperform MASTER and other random restarting approaches.

Track-MDP: Reinforcement Learning for Target Tracking with Controlled Sensing

State of the art methods for target tracking with sensor management (or controlled sensing) are model-based and are obtained through solutions to Partially Observable Markov Decision Process (POMDP) formulations. In this paper a Reinforcement Learning (RL) approach to the problem is explored for the setting where the motion model for the object/target to be tracked is unknown to the observer. It is assumed that the target dynamics are stationary in time, the state space and the observation space are discrete, and there is complete observability of the location of the target under certain (a priori unknown) sensor control actions. Then, a novel Markov Decision Process (MDP) rather than POMDP formulation is proposed for the tracking problem with controlled sensing, which is termed as Track-MDP. In contrast to the POMDP formulation, the Track-MDP formulation is amenable to an RL based solution. It is shown that the optimal policy for the Track-MDP formulation, which is approximated through RL, is guaranteed to track all significant target paths with certainty. The Track-MDP method is then compared with the optimal POMDP policy, and it is shown that the infinite horizon tracking reward of the optimal Track-MDP policy is the same as that of the optimal POMDP policy. In simulations it is demonstrated that Track-MDP based RL leads to a policy that can track the target with high accuracy.