Is Prior-Free Black-Box Non-Stationary Reinforcement Learning Feasible?
Paper and Code
Oct 17, 2024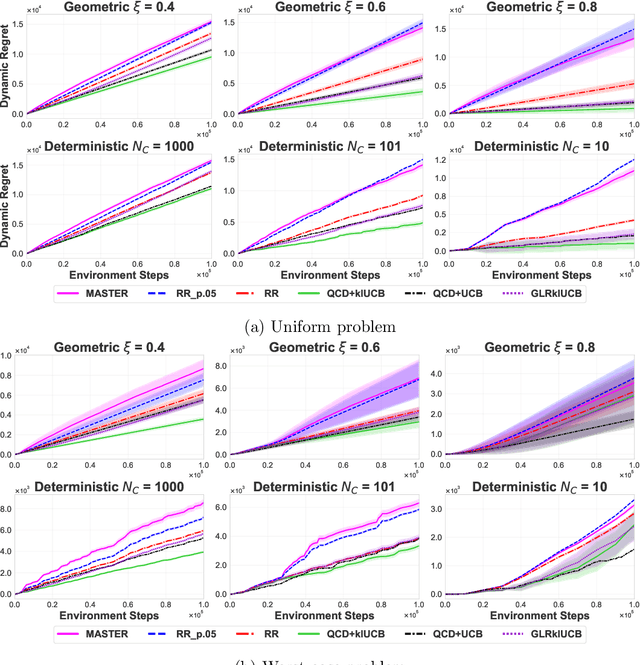
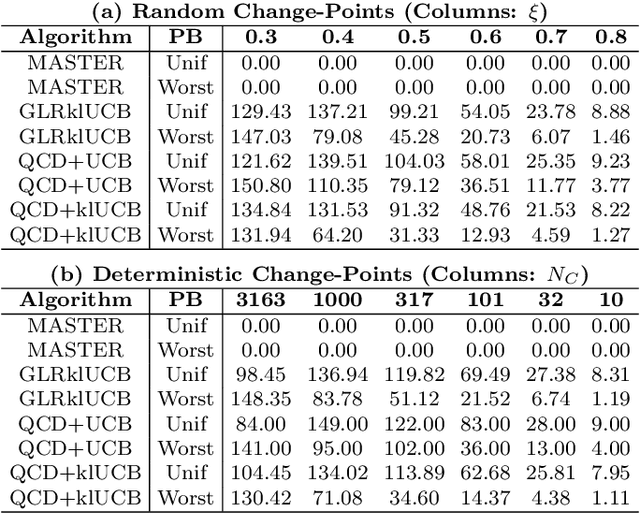
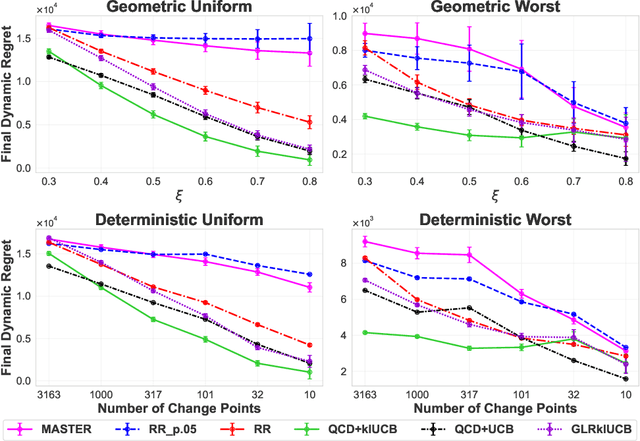
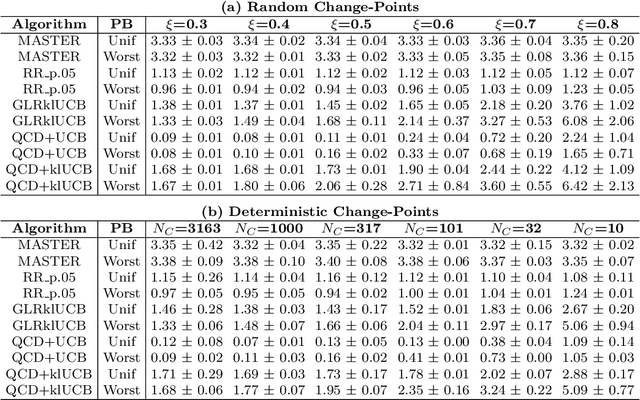
We study the problem of Non-Stationary Reinforcement Learning (NS-RL) without prior knowledge about the system's non-stationarity. A state-of-the-art, black-box algorithm, known as MASTER, is considered, with a focus on identifying the conditions under which it can achieve its stated goals. Specifically, we prove that MASTER's non-stationarity detection mechanism is not triggered for practical choices of horizon, leading to performance akin to a random restarting algorithm. Moreover, we show that the regret bound for MASTER, while being order optimal, stays above the worst-case linear regret until unreasonably large values of the horizon. To validate these observations, MASTER is tested for the special case of piecewise stationary multi-armed bandits, along with methods that employ random restarting, and others that use quickest change detection to restart. A simple, order optimal random restarting algorithm, that has prior knowledge of the non-stationarity is proposed as a baseline. The behavior of the MASTER algorithm is validated in simulations, and it is shown that methods employing quickest change detection are more robust and consistently outperform MASTER and other random restarting approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge