Detection Is All You Need: A Feasible Optimal Prior-Free Black-Box Approach For Piecewise Stationary Bandits

We study the problem of piecewise stationary bandits without prior knowledge of the underlying non-stationarity. We propose the first $\textit{feasible}$ black-box algorithm applicable to most common parametric bandit variants. Our procedure, termed Detection Augmented Bandit (DAB), is modular, accepting any stationary bandit algorithm as input and augmenting it with a change detector. DAB achieves optimal regret in the piecewise stationary setting under mild assumptions. Specifically, we prove that DAB attains the order-optimal regret bound of $\tilde{\mathcal{O}}(\sqrt{N_T T})$, where $N_T$ denotes the number of changes over the horizon $T$, if its input stationary bandit algorithm has order-optimal stationary regret guarantees. Applying DAB to different parametric bandit settings, we recover recent state-of-the-art results. Notably, for self-concordant bandits, DAB achieves optimal dynamic regret, while previous works obtain suboptimal bounds and require knowledge on the non-stationarity. In simulations on piecewise stationary environments, DAB outperforms existing approaches across varying number of changes. Interestingly, despite being theoretically designed for piecewise stationary environments, DAB is also effective in simulations in drifting environments, outperforming existing methods designed specifically for this scenario.

Nonparametric Sparse Online Learning of the Koopman Operator

The Koopman operator provides a powerful framework for representing the dynamics of general nonlinear dynamical systems. Data-driven techniques to learn the Koopman operator typically assume that the chosen function space is closed under system dynamics. In this paper, we study the Koopman operator via its action on the reproducing kernel Hilbert space (RKHS), and explore the mis-specified scenario where the dynamics may escape the chosen function space. We relate the Koopman operator to the conditional mean embeddings (CME) operator and then present an operator stochastic approximation algorithm to learn the Koopman operator iteratively with control over the complexity of the representation. We provide both asymptotic and finite-time last-iterate guarantees of the online sparse learning algorithm with trajectory-based sampling with an analysis that is substantially more involved than that for finite-dimensional stochastic approximation. Numerical examples confirm the effectiveness of the proposed algorithm.

Change Detection-Based Procedures for Piecewise Stationary MABs: A Modular Approach

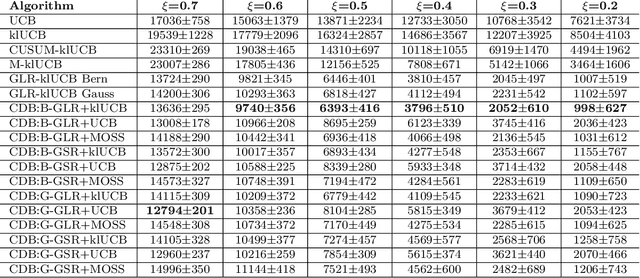
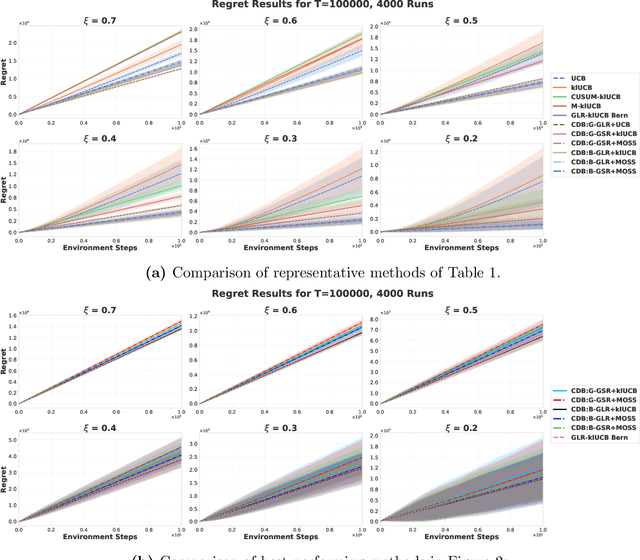
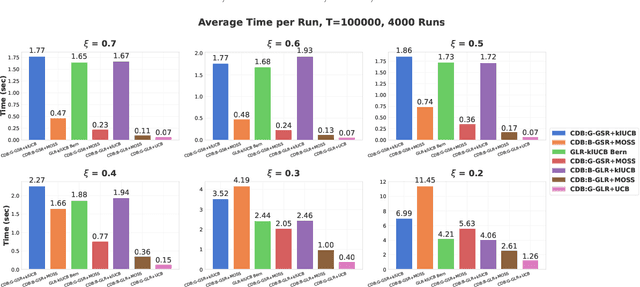
Conventional Multi-Armed Bandit (MAB) algorithms are designed for stationary environments, where the reward distributions associated with the arms do not change with time. In many applications, however, the environment is more accurately modeled as being nonstationary. In this work, piecewise stationary MAB (PS-MAB) environments are investigated, in which the reward distributions associated with a subset of the arms change at some change-points and remain stationary between change-points. Our focus is on the asymptotic analysis of PS-MABs, for which practical algorithms based on change detection (CD) have been previously proposed. Our goal is to modularize the design and analysis of such CD-based Bandit (CDB) procedures. To this end, we identify the requirements for stationary bandit algorithms and change detectors in a CDB procedure that are needed for the modularization. We assume that the rewards are sub-Gaussian. Under this assumption and a condition on the separation of the change-points, we show that the analysis of CDB procedures can indeed be modularized, so that regret bounds can be obtained in a unified manner for various combinations of change detectors and bandit algorithms. Through this analysis, we develop new modular CDB procedures that are order-optimal. We compare the performance of our modular CDB procedures with various other methods in simulations.

Tangential Randomization in Linear Bandits (TRAiL): Guaranteed Inference and Regret Bounds

We propose and analyze TRAiL (Tangential Randomization in Linear Bandits), a computationally efficient regret-optimal forced exploration algorithm for linear bandits on action sets that are sublevel sets of strongly convex functions. TRAiL estimates the governing parameter of the linear bandit problem through a standard regularized least squares and perturbs the reward-maximizing action corresponding to said point estimate along the tangent plane of the convex compact action set before projecting back to it. Exploiting concentration results for matrix martingales, we prove that TRAiL ensures a $\Omega(\sqrt{T})$ growth in the inference quality, measured via the minimum eigenvalue of the design (regressor) matrix with high-probability over a $T$-length period. We build on this result to obtain an $\mathcal{O}(\sqrt{T} \log(T))$ upper bound on cumulative regret with probability at least $ 1 - 1/T$ over $T$ periods, and compare TRAiL to other popular algorithms for linear bandits. Then, we characterize an $\Omega(\sqrt{T})$ minimax lower bound for any algorithm on the expected regret that covers a wide variety of action/parameter sets and noise processes. Our analysis not only expands the realm of lower-bounds in linear bandits significantly, but as a byproduct, yields a trade-off between regret and inference quality. Specifically, we prove that any algorithm with an $\mathcal{O}(T^\alpha)$ expected regret growth must have an $\Omega(T^{1-\alpha})$ asymptotic growth in expected inference quality. Our experiments on the $L^p$ unit ball as action sets reveal how this relation can be violated, but only in the short-run, before returning to respect the bound asymptotically. In effect, regret-minimizing algorithms must have just the right rate of inference -- too fast or too slow inference will incur sub-optimal regret growth.

Compressed Online Learning of Conditional Mean Embedding

The conditional mean embedding (CME) encodes Markovian stochastic kernels through their actions on probability distributions embedded within the reproducing kernel Hilbert spaces (RKHS). The CME plays a key role in several well-known machine learning tasks such as reinforcement learning, analysis of dynamical systems, etc. We present an algorithm to learn the CME incrementally from data via an operator-valued stochastic gradient descent. As is well-known, function learning in RKHS suffers from scalability challenges from large data. We utilize a compression mechanism to counter the scalability challenge. The core contribution of this paper is a finite-sample performance guarantee on the last iterate of the online compressed operator learning algorithm with fast-mixing Markovian samples, when the target CME may not be contained in the hypothesis space. We illustrate the efficacy of our algorithm by applying it to the analysis of an example dynamical system.