Track-MDP: Reinforcement Learning for Target Tracking with Controlled Sensing

State of the art methods for target tracking with sensor management (or controlled sensing) are model-based and are obtained through solutions to Partially Observable Markov Decision Process (POMDP) formulations. In this paper a Reinforcement Learning (RL) approach to the problem is explored for the setting where the motion model for the object/target to be tracked is unknown to the observer. It is assumed that the target dynamics are stationary in time, the state space and the observation space are discrete, and there is complete observability of the location of the target under certain (a priori unknown) sensor control actions. Then, a novel Markov Decision Process (MDP) rather than POMDP formulation is proposed for the tracking problem with controlled sensing, which is termed as Track-MDP. In contrast to the POMDP formulation, the Track-MDP formulation is amenable to an RL based solution. It is shown that the optimal policy for the Track-MDP formulation, which is approximated through RL, is guaranteed to track all significant target paths with certainty. The Track-MDP method is then compared with the optimal POMDP policy, and it is shown that the infinite horizon tracking reward of the optimal Track-MDP policy is the same as that of the optimal POMDP policy. In simulations it is demonstrated that Track-MDP based RL leads to a policy that can track the target with high accuracy.

Adaptive Step-Size Methods for Compressed SGD

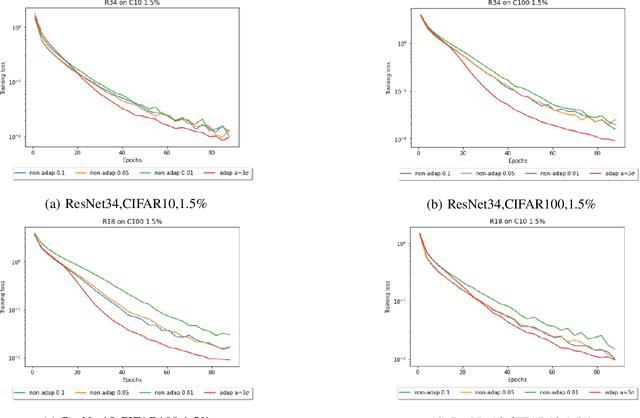
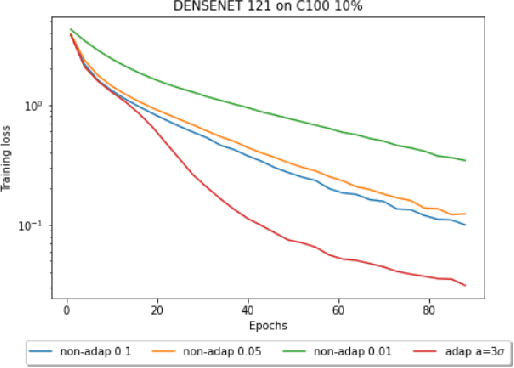
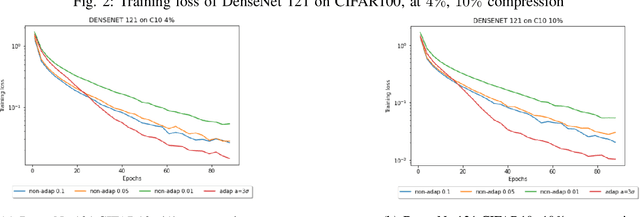
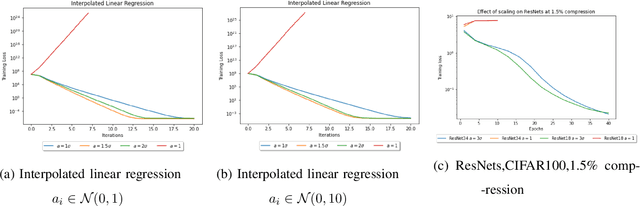
Compressed Stochastic Gradient Descent (SGD) algorithms have been recently proposed to address the communication bottleneck in distributed and decentralized optimization problems, such as those that arise in federated machine learning. Existing compressed SGD algorithms assume the use of non-adaptive step-sizes(constant or diminishing) to provide theoretical convergence guarantees. Typically, the step-sizes are fine-tuned in practice to the dataset and the learning algorithm to provide good empirical performance. Such fine-tuning might be impractical in many learning scenarios, and it is therefore of interest to study compressed SGD using adaptive step-sizes. Motivated by prior work on adaptive step-size methods for SGD to train neural networks efficiently in the uncompressed setting, we develop an adaptive step-size method for compressed SGD. In particular, we introduce a scaling technique for the descent step in compressed SGD, which we use to establish order-optimal convergence rates for convex-smooth and strong convex-smooth objectives under an interpolation condition and for non-convex objectives under a strong growth condition. We also show through simulation examples that without this scaling, the algorithm can fail to converge. We present experimental results on deep neural networks for real-world datasets, and compare the performance of our proposed algorithm with previously proposed compressed SGD methods in literature, and demonstrate improved performance on ResNet-18, ResNet-34 and DenseNet architectures for CIFAR-100 and CIFAR-10 datasets at various levels of compression.