Adaptive Step-Size Methods for Compressed SGD

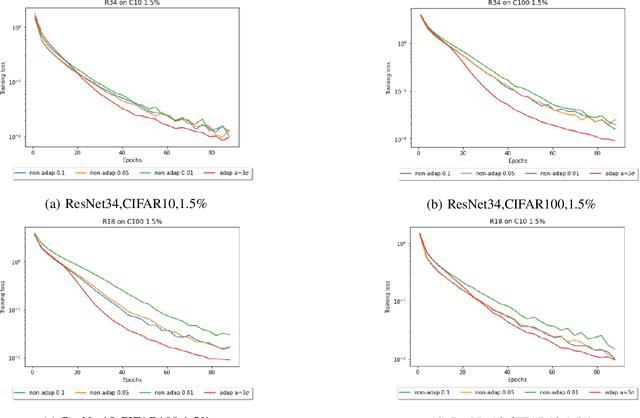
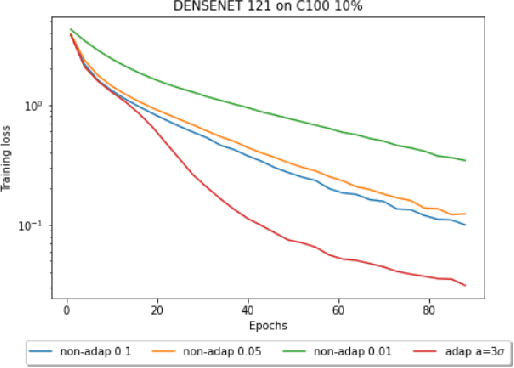
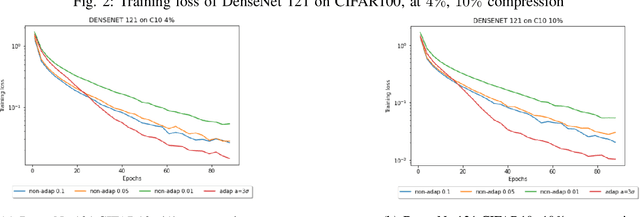
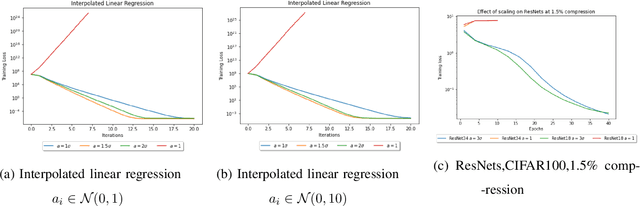
Compressed Stochastic Gradient Descent (SGD) algorithms have been recently proposed to address the communication bottleneck in distributed and decentralized optimization problems, such as those that arise in federated machine learning. Existing compressed SGD algorithms assume the use of non-adaptive step-sizes(constant or diminishing) to provide theoretical convergence guarantees. Typically, the step-sizes are fine-tuned in practice to the dataset and the learning algorithm to provide good empirical performance. Such fine-tuning might be impractical in many learning scenarios, and it is therefore of interest to study compressed SGD using adaptive step-sizes. Motivated by prior work on adaptive step-size methods for SGD to train neural networks efficiently in the uncompressed setting, we develop an adaptive step-size method for compressed SGD. In particular, we introduce a scaling technique for the descent step in compressed SGD, which we use to establish order-optimal convergence rates for convex-smooth and strong convex-smooth objectives under an interpolation condition and for non-convex objectives under a strong growth condition. We also show through simulation examples that without this scaling, the algorithm can fail to converge. We present experimental results on deep neural networks for real-world datasets, and compare the performance of our proposed algorithm with previously proposed compressed SGD methods in literature, and demonstrate improved performance on ResNet-18, ResNet-34 and DenseNet architectures for CIFAR-100 and CIFAR-10 datasets at various levels of compression.

Multiple Testing Framework for Out-of-Distribution Detection

We study the problem of Out-of-Distribution (OOD) detection, that is, detecting whether a learning algorithm's output can be trusted at inference time. While a number of tests for OOD detection have been proposed in prior work, a formal framework for studying this problem is lacking. We propose a definition for the notion of OOD that includes both the input distribution and the learning algorithm, which provides insights for the construction of powerful tests for OOD detection. We propose a multiple hypothesis testing inspired procedure to systematically combine any number of different statistics from the learning algorithm using conformal p-values. We further provide strong guarantees on the probability of incorrectly classifying an in-distribution sample as OOD. In our experiments, we find that threshold-based tests proposed in prior work perform well in specific settings, but not uniformly well across different types of OOD instances. In contrast, our proposed method that combines multiple statistics performs uniformly well across different datasets and neural networks.

Group Equivariant Neural Architecture Search via Group Decomposition and Reinforcement Learning

Recent works show that including group equivariance as an inductive bias improves neural network performance for both classification and generation tasks. Designing group-equivariant neural networks is, however, challenging when the group of interest is large and is unknown. Moreover, inducing equivariance can significantly reduce the number of independent parameters in a network with fixed feature size, affecting its overall performance. We address these problems by proving a new group-theoretic result in the context of equivariant neural networks that shows that a network is equivariant to a large group if and only if it is equivariant to smaller groups from which it is constructed. We also design an algorithm to construct equivariant networks that significantly improves computational complexity. Further, leveraging our theoretical result, we use deep Q-learning to search for group equivariant networks that maximize performance, in a significantly reduced search space than naive approaches, yielding what we call autoequivariant networks (AENs). To evaluate AENs, we construct and release new benchmark datasets, G-MNIST and G-Fashion-MNIST, obtained via group transformations on MNIST and Fashion-MNIST respectively. We show that AENs find the right balance between group equivariance and number of parameters, thereby consistently having good task performance.

Dynamic Spectrum Access using Stochastic Multi-User Bandits

A stochastic multi-user multi-armed bandit framework is used to develop algorithms for uncoordinated spectrum access. In contrast to prior work, it is assumed that rewards can be non-zero even under collisions, thus allowing for the number of users to be greater than the number of channels. The proposed algorithm consists of an estimation phase and an allocation phase. It is shown that if every user adopts the algorithm, the system wide regret is order-optimal of order $O(\log T)$ over a time-horizon of duration $T$. The regret guarantees hold for both the cases where the number of users is greater than or less than the number of channels. The algorithm is extended to the dynamic case where the number of users in the system evolves over time, and is shown to lead to sub-linear regret.

Multi-User MABs with User Dependent Rewards for Uncoordinated Spectrum Access

Multi-user multi-armed bandits have emerged as a good model for uncoordinated spectrum access problems. In this paper we consider the scenario where users cannot communicate with each other. In addition, the environment may appear differently to different users, ${i.e.}$, the mean rewards as observed by different users for the same channel may be different. With this setup, we present a policy that achieves a regret of $O (\log{T})$. This paper has been accepted at Asilomar Conference on Signals, Systems, and Computers 2019.

Multi-player Multi-Armed Bandits with non-zero rewards on collisions for uncoordinated spectrum access

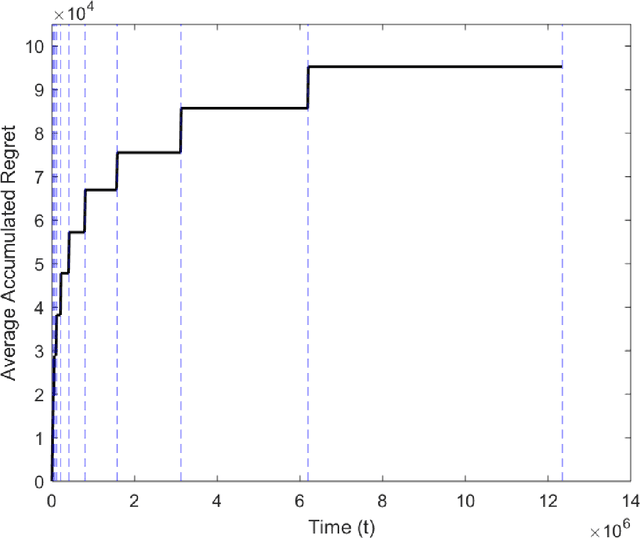
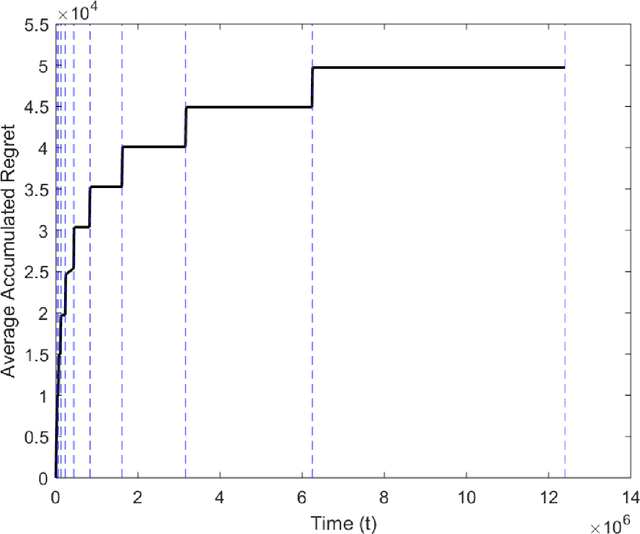
In this paper, we study the uncoordinated spectrum access problem using the multi-player multi-armed bandits framework. We consider a model where there is no central control and the users cannot communicate with each other. The environment may appear differently to different users, \textit{i.e.}, the mean rewards as seen by different users for a particular channel may be different. Additionally, in case of a collision, we allow for the colliding users to receive non-zero rewards. With this setup, we present a policy that achieves expected regret of order $O(\log^{2+\delta}{T})$ for some $\delta > 0$.