G-RepsNet: A Fast and General Construction of Equivariant Networks for Arbitrary Matrix Groups

Group equivariance is a strong inductive bias useful in a wide range of deep learning tasks. However, constructing efficient equivariant networks for general groups and domains is difficult. Recent work by Finzi et al. (2021) directly solves the equivariance constraint for arbitrary matrix groups to obtain equivariant MLPs (EMLPs). But this method does not scale well and scaling is crucial in deep learning. Here, we introduce Group Representation Networks (G-RepsNets), a lightweight equivariant network for arbitrary matrix groups with features represented using tensor polynomials. The key intuition for our design is that using tensor representations in the hidden layers of a neural network along with simple inexpensive tensor operations can lead to expressive universal equivariant networks. We find G-RepsNet to be competitive to EMLP on several tasks with group symmetries such as O(5), O(1, 3), and O(3) with scalars, vectors, and second-order tensors as data types. On image classification tasks, we find that G-RepsNet using second-order representations is competitive and often even outperforms sophisticated state-of-the-art equivariant models such as GCNNs (Cohen & Welling, 2016a) and E(2)-CNNs (Weiler & Cesa, 2019). To further illustrate the generality of our approach, we show that G-RepsNet is competitive to G-FNO (Helwig et al., 2023) and EGNN (Satorras et al., 2021) on N-body predictions and solving PDEs, respectively, while being efficient.

Efficient Model-Agnostic Multi-Group Equivariant Networks

Constructing model-agnostic group equivariant networks, such as equitune (Basu et al., 2023b) and its generalizations (Kim et al., 2023), can be computationally expensive for large product groups. We address this by providing efficient model-agnostic equivariant designs for two related problems: one where the network has multiple inputs each with potentially different groups acting on them, and another where there is a single input but the group acting on it is a large product group. For the first design, we initially consider a linear model and characterize the entire equivariant space that satisfies this constraint. This characterization gives rise to a novel fusion layer between different channels that satisfies an invariance-symmetry (IS) constraint, which we call an IS layer. We then extend this design beyond linear models, similar to equitune, consisting of equivariant and IS layers. We also show that the IS layer is a universal approximator of invariant-symmetric functions. Inspired by the first design, we use the notion of the IS property to design a second efficient model-agnostic equivariant design for large product groups acting on a single input. For the first design, we provide experiments on multi-image classification where each view is transformed independently with transformations such as rotations. We find equivariant models are robust to such transformations and perform competitively otherwise. For the second design, we consider three applications: language compositionality on the SCAN dataset to product groups; fairness in natural language generation from GPT-2 to address intersectionality; and robust zero-shot image classification with CLIP. Overall, our methods are simple and general, competitive with equitune and its variants, while also being computationally more efficient.

Transformers are Universal Predictors

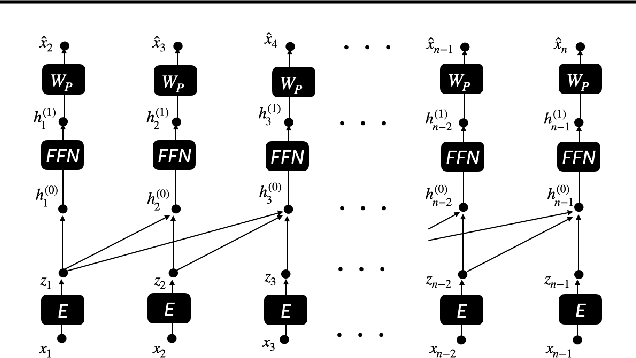
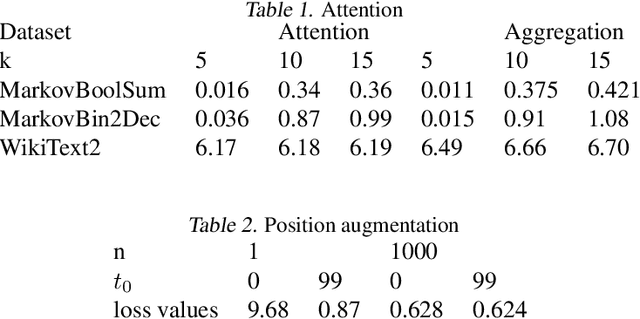
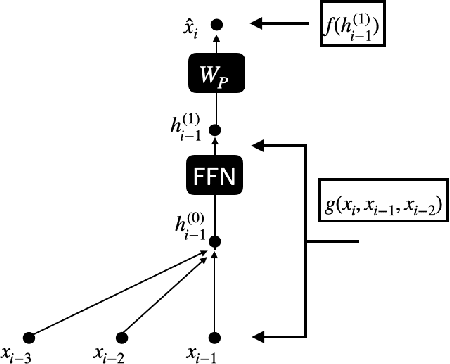
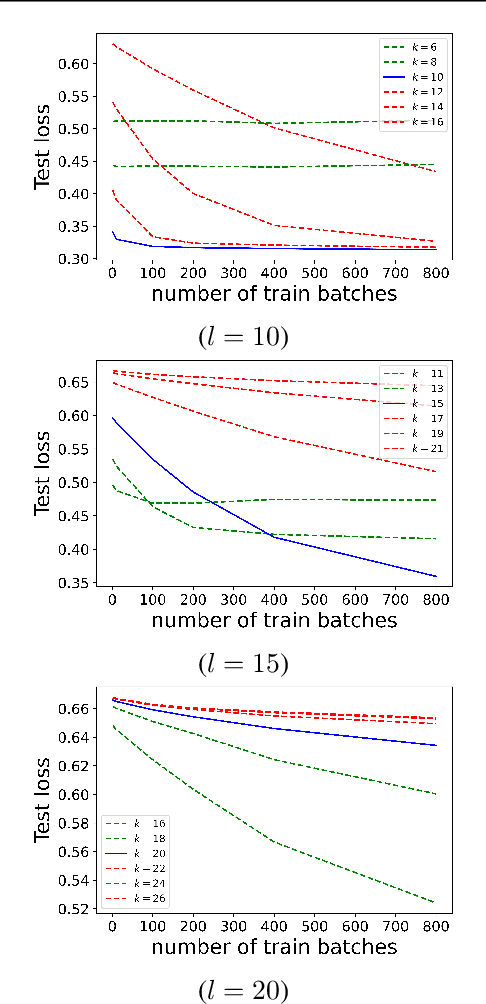
We find limits to the Transformer architecture for language modeling and show it has a universal prediction property in an information-theoretic sense. We further analyze performance in non-asymptotic data regimes to understand the role of various components of the Transformer architecture, especially in the context of data-efficient training. We validate our theoretical analysis with experiments on both synthetic and real datasets.

Equivariant Few-Shot Learning from Pretrained Models

Efficient transfer learning algorithms are key to the success of foundation models on diverse downstream tasks even with limited data. Recent works of \cite{basu2022equi} and \cite{kaba2022equivariance} propose group averaging (\textit{equitune}) and optimization-based methods, respectively, over features from group-transformed inputs to obtain equivariant outputs from non-equivariant neural networks. While \cite{kaba2022equivariance} are only concerned with training from scratch, we find that equitune performs poorly on equivariant zero-shot tasks despite good finetuning results. We hypothesize that this is because pretrained models provide better quality features for certain transformations than others and simply averaging them is deleterious. Hence, we propose $\lambda$-\textit{equitune} that averages the features using \textit{importance weights}, $\lambda$s. These weights are learned directly from the data using a small neural network, leading to excellent zero-shot and finetuned results that outperform equitune. Further, we prove that $\lambda$-equitune is equivariant and a universal approximator of equivariant functions. Additionally, we show that the method of \cite{kaba2022equivariance} used with appropriate loss functions, which we call \textit{equizero}, also gives excellent zero-shot and finetuned performance. Both equitune and equizero are special cases of $\lambda$-equitune. To show the simplicity and generality of our method, we validate on a wide range of diverse applications and models such as 1) image classification using CLIP, 2) deep Q-learning, 3) fairness in natural language generation (NLG), 4) compositional generalization in languages, and 5) image classification using pretrained CNNs such as Resnet and Alexnet.

Equi-Tuning: Group Equivariant Fine-Tuning of Pretrained Models

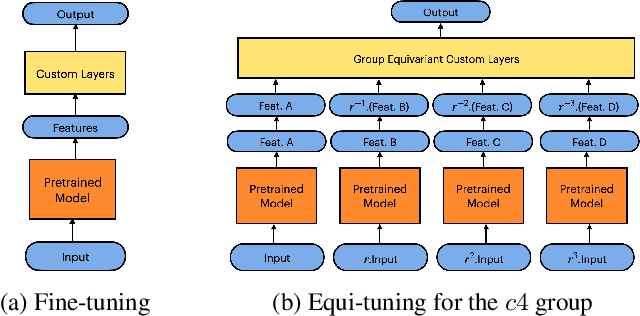
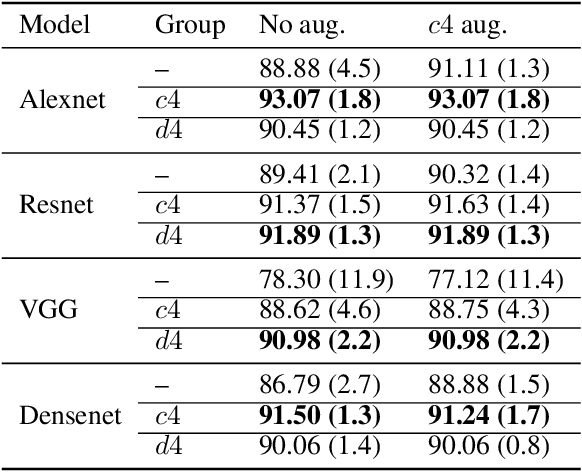
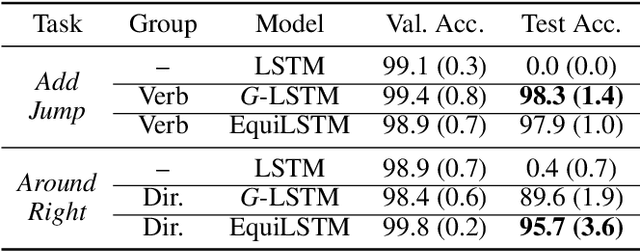
We introduce equi-tuning, a novel fine-tuning method that transforms (potentially non-equivariant) pretrained models into group equivariant models while incurring minimum $L_2$ loss between the feature representations of the pretrained and the equivariant models. Large pretrained models can be equi-tuned for different groups to satisfy the needs of various downstream tasks. Equi-tuned models benefit from both group equivariance as an inductive bias and semantic priors from pretrained models. We provide applications of equi-tuning on three different tasks: image classification, compositional generalization in language, and fairness in natural language generation (NLG). We also provide a novel group-theoretic definition for fairness in NLG. The effectiveness of this definition is shown by testing it against a standard empirical method of fairness in NLG. We provide experimental results for equi-tuning using a variety of pretrained models: Alexnet, Resnet, VGG, and Densenet for image classification; RNNs, GRUs, and LSTMs for compositional generalization; and GPT2 for fairness in NLG. We test these models on benchmark datasets across all considered tasks to show the generality and effectiveness of the proposed method.

Equivariant Mesh Attention Networks

Equivariance to symmetries has proven to be a powerful inductive bias in deep learning research. Recent works on mesh processing have concentrated on various kinds of natural symmetries, including translations, rotations, scaling, node permutations, and gauge transformations. To date, no existing architecture is equivariant to all of these transformations. Moreover, previous implementations have not always applied these symmetry transformations to the test dataset. This inhibits the ability to determine whether the model attains the claimed equivariance properties. In this paper, we present an attention-based architecture for mesh data that is provably equivariant to all transformations mentioned above. We carry out experiments on the FAUST and TOSCA datasets, and apply the mentioned symmetries to the test set only. Our results confirm that our proposed architecture is equivariant, and therefore robust, to these local/global transformations.

Group Equivariant Neural Architecture Search via Group Decomposition and Reinforcement Learning

Recent works show that including group equivariance as an inductive bias improves neural network performance for both classification and generation tasks. Designing group-equivariant neural networks is, however, challenging when the group of interest is large and is unknown. Moreover, inducing equivariance can significantly reduce the number of independent parameters in a network with fixed feature size, affecting its overall performance. We address these problems by proving a new group-theoretic result in the context of equivariant neural networks that shows that a network is equivariant to a large group if and only if it is equivariant to smaller groups from which it is constructed. We also design an algorithm to construct equivariant networks that significantly improves computational complexity. Further, leveraging our theoretical result, we use deep Q-learning to search for group equivariant networks that maximize performance, in a significantly reduced search space than naive approaches, yielding what we call autoequivariant networks (AENs). To evaluate AENs, we construct and release new benchmark datasets, G-MNIST and G-Fashion-MNIST, obtained via group transformations on MNIST and Fashion-MNIST respectively. We show that AENs find the right balance between group equivariance and number of parameters, thereby consistently having good task performance.

Mirostat: A Perplexity-Controlled Neural Text Decoding Algorithm

Neural text decoding is important for generating high-quality texts using language models. To generate high-quality text, popular decoding algorithms like top-k, top-p (nucleus), and temperature-based sampling truncate or distort the unreliable low probability tail of the language model. Though these methods generate high-quality text after parameter tuning, they are ad hoc. Not much is known about the control they provide over the statistics of the output, which is important since recent reports show text quality is highest for a specific range of likelihoods. Here, first we provide a theoretical analysis of perplexity in top-k, top-p, and temperature sampling, finding that cross-entropy behaves approximately linearly as a function of p in top-p sampling whereas it is a nonlinear function of k in top-k sampling, under Zipfian statistics. We use this analysis to design a feedback-based adaptive top-k text decoding algorithm called mirostat that generates text (of any length) with a predetermined value of perplexity, and thereby high-quality text without any tuning. Experiments show that for low values of k and p in top-k and top-p sampling, perplexity drops significantly with generated text length, which is also correlated with excessive repetitions in the text (the boredom trap). On the other hand, for large values of k and p, we find that perplexity increases with generated text length, which is correlated with incoherence in the text (confusion trap). Mirostat avoids both traps: experiments show that cross-entropy has a near-linear relation with repetition in generated text. This relation is almost independent of the sampling method but slightly dependent on the model used. Hence, for a given language model, control over perplexity also gives control over repetitions.

Universal and Succinct Source Coding of Deep Neural Networks

Deep neural networks have shown incredible performance for inference tasks in a variety of domains. Unfortunately, most current deep networks are enormous cloud-based structures that require significant storage space, which limits scaling of deep learning as a service (DLaaS) and use for on-device augmented intelligence. This paper is concerned with finding universal lossless compressed representations of deep feedforward networks with synaptic weights drawn from discrete sets, and directly performing inference without full decompression. The basic insight that allows less rate than naive approaches is the recognition that the bipartite graph layers of feedforward networks have a kind of permutation invariance to the labeling of nodes, in terms of inferential operation. We provide efficient algorithms to dissipate this irrelevant uncertainty and then use arithmetic coding to nearly achieve the entropy bound in a universal manner. We also provide experimental results of our approach on the MNIST dataset.