Lie Algebra Canonicalization: Equivariant Neural Operators under arbitrary Lie Groups

The quest for robust and generalizable machine learning models has driven recent interest in exploiting symmetries through equivariant neural networks. In the context of PDE solvers, recent works have shown that Lie point symmetries can be a useful inductive bias for Physics-Informed Neural Networks (PINNs) through data and loss augmentation. Despite this, directly enforcing equivariance within the model architecture for these problems remains elusive. This is because many PDEs admit non-compact symmetry groups, oftentimes not studied beyond their infinitesimal generators, making them incompatible with most existing equivariant architectures. In this work, we propose Lie aLgebrA Canonicalization (LieLAC), a novel approach that exploits only the action of infinitesimal generators of the symmetry group, circumventing the need for knowledge of the full group structure. To achieve this, we address existing theoretical issues in the canonicalization literature, establishing connections with frame averaging in the case of continuous non-compact groups. Operating within the framework of canonicalization, LieLAC can easily be integrated with unconstrained pre-trained models, transforming inputs to a canonical form before feeding them into the existing model, effectively aligning the input for model inference according to allowed symmetries. LieLAC utilizes standard Lie group descent schemes, achieving equivariance in pre-trained models. Finally, we showcase LieLAC's efficacy on tasks of invariant image classification and Lie point symmetry equivariant neural PDE solvers using pre-trained models.

G-Adaptive mesh refinement -- leveraging graph neural networks and differentiable finite element solvers

We present a novel, and effective, approach to the long-standing problem of mesh adaptivity in finite element methods (FEM). FE solvers are powerful tools for solving partial differential equations (PDEs), but their cost and accuracy are critically dependent on the choice of mesh points. To keep computational costs low, mesh relocation (r-adaptivity) seeks to optimise the position of a fixed number of mesh points to obtain the best FE solution accuracy. Classical approaches to this problem require the solution of a separate nonlinear "meshing" PDE to find the mesh point locations. This incurs significant cost at remeshing and relies on certain a-priori assumptions and guiding heuristics for optimal mesh point location. Recent machine learning approaches to r-adaptivity have mainly focused on the construction of fast surrogates for such classical methods. Our new approach combines a graph neural network (GNN) powered architecture, with training based on direct minimisation of the FE solution error with respect to the mesh point locations. The GNN employs graph neural diffusion (GRAND), closely aligning the mesh solution space to that of classical meshing methodologies, thus replacing heuristics with a learnable strategy, and providing a strong inductive bias. This allows for rapid and robust training and results in an extremely efficient and effective GNN approach to online r-adaptivity. This method outperforms classical and prior ML approaches to r-adaptive meshing on the test problems we consider, in particular achieving lower FE solution error, whilst retaining the significant speed-up over classical methods observed in prior ML work.

Graph Neural Networks as Gradient Flows

Dynamical systems minimizing an energy are ubiquitous in geometry and physics. We propose a gradient flow framework for GNNs where the equations follow the direction of steepest descent of a learnable energy. This approach allows to explain the GNN evolution from a multi-particle perspective as learning attractive and repulsive forces in feature space via the positive and negative eigenvalues of a symmetric "channel-mixing" matrix. We perform spectral analysis of the solutions and conclude that gradient flow graph convolutional models can induce a dynamics dominated by the graph high frequencies which is desirable for heterophilic datasets. We also describe structural constraints on common GNN architectures allowing to interpret them as gradient flows. We perform thorough ablation studies corroborating our theoretical analysis and show competitive performance of simple and lightweight models on real-world homophilic and heterophilic datasets.

Equivariant Mesh Attention Networks

Equivariance to symmetries has proven to be a powerful inductive bias in deep learning research. Recent works on mesh processing have concentrated on various kinds of natural symmetries, including translations, rotations, scaling, node permutations, and gauge transformations. To date, no existing architecture is equivariant to all of these transformations. Moreover, previous implementations have not always applied these symmetry transformations to the test dataset. This inhibits the ability to determine whether the model attains the claimed equivariance properties. In this paper, we present an attention-based architecture for mesh data that is provably equivariant to all transformations mentioned above. We carry out experiments on the FAUST and TOSCA datasets, and apply the mentioned symmetries to the test set only. Our results confirm that our proposed architecture is equivariant, and therefore robust, to these local/global transformations.

Graph-Coupled Oscillator Networks

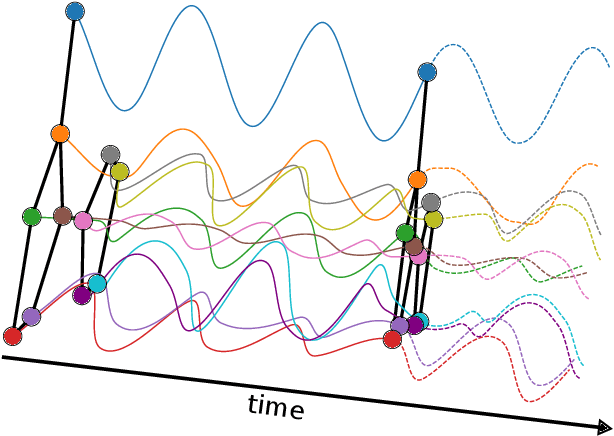
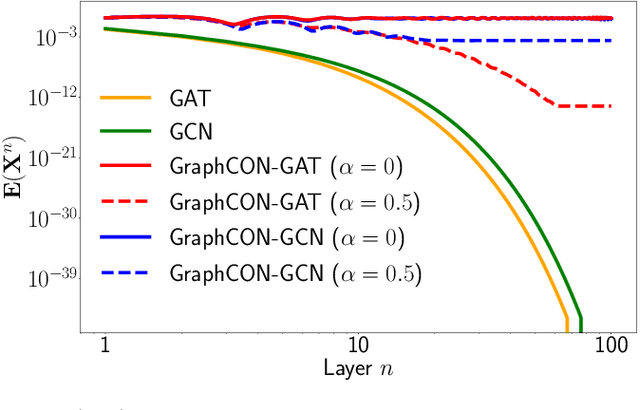
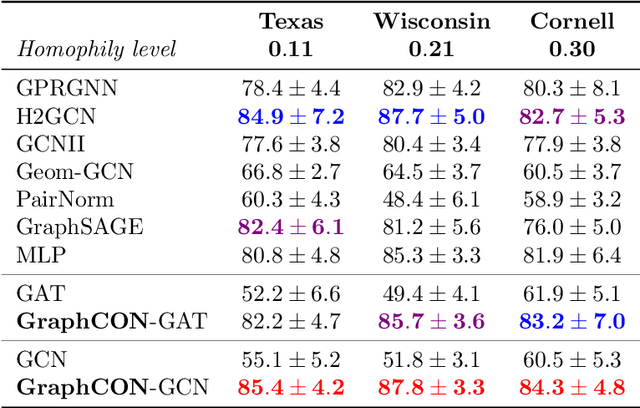
We propose Graph-Coupled Oscillator Networks (GraphCON), a novel framework for deep learning on graphs. It is based on discretizations of a second-order system of ordinary differential equations (ODEs), which model a network of nonlinear forced and damped oscillators, coupled via the adjacency structure of the underlying graph. The flexibility of our framework permits any basic GNN layer (e.g. convolutional or attentional) as the coupling function, from which a multi-layer deep neural network is built up via the dynamics of the proposed ODEs. We relate the oversmoothing problem, commonly encountered in GNNs, to the stability of steady states of the underlying ODE and show that zero-Dirichlet energy steady states are not stable for our proposed ODEs. This demonstrates that the proposed framework mitigates the oversmoothing problem. Finally, we show that our approach offers competitive performance with respect to the state-of-the-art on a variety of graph-based learning tasks.

Beltrami Flow and Neural Diffusion on Graphs

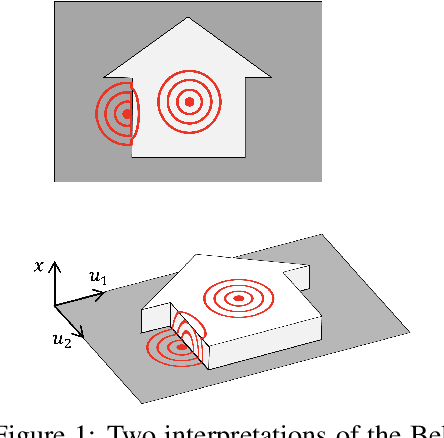
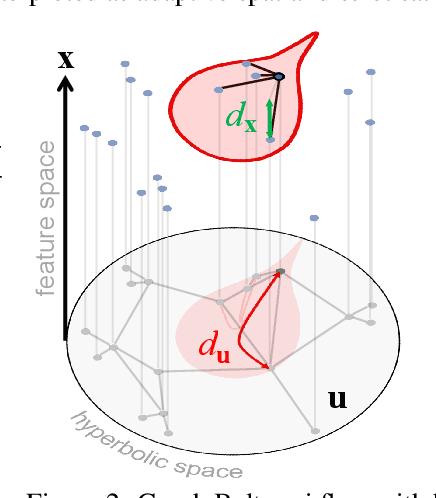
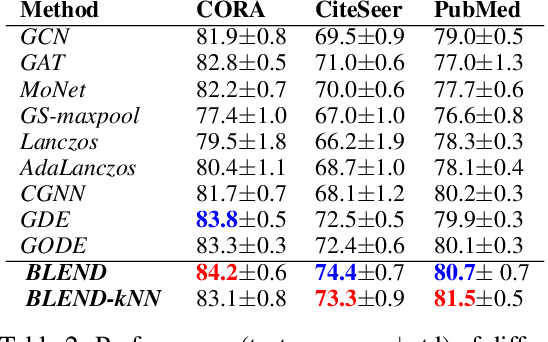
We propose a novel class of graph neural networks based on the discretised Beltrami flow, a non-Euclidean diffusion PDE. In our model, node features are supplemented with positional encodings derived from the graph topology and jointly evolved by the Beltrami flow, producing simultaneously continuous feature learning and topology evolution. The resulting model generalises many popular graph neural networks and achieves state-of-the-art results on several benchmarks.

GRAND: Graph Neural Diffusion

We present Graph Neural Diffusion (GRAND) that approaches deep learning on graphs as a continuous diffusion process and treats Graph Neural Networks (GNNs) as discretisations of an underlying PDE. In our model, the layer structure and topology correspond to the discretisation choices of temporal and spatial operators. Our approach allows a principled development of a broad new class of GNNs that are able to address the common plights of graph learning models such as depth, oversmoothing, and bottlenecks. Key to the success of our models are stability with respect to perturbations in the data and this is addressed for both implicit and explicit discretisation schemes. We develop linear and nonlinear versions of GRAND, which achieve competitive results on many standard graph benchmarks.