Graph Neural Networks for Link Prediction with Subgraph Sketching

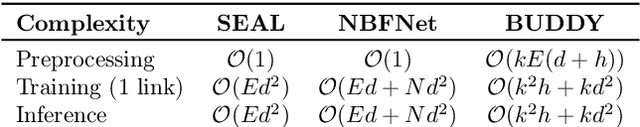
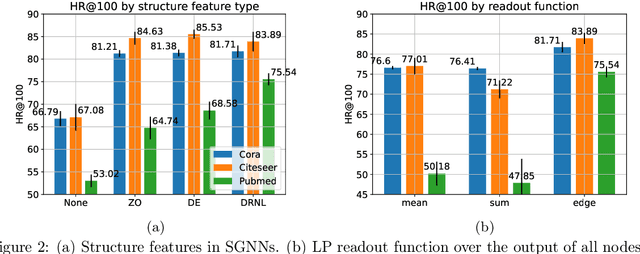
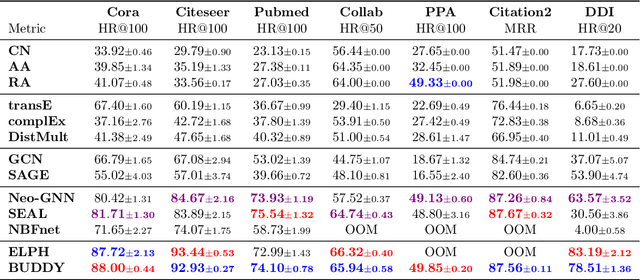
Many Graph Neural Networks (GNNs) perform poorly compared to simple heuristics on Link Prediction (LP) tasks. This is due to limitations in expressive power such as the inability to count triangles (the backbone of most LP heuristics) and because they can not distinguish automorphic nodes (those having identical structural roles). Both expressiveness issues can be alleviated by learning link (rather than node) representations and incorporating structural features such as triangle counts. Since explicit link representations are often prohibitively expensive, recent works resorted to subgraph-based methods, which have achieved state-of-the-art performance for LP, but suffer from poor efficiency due to high levels of redundancy between subgraphs. We analyze the components of subgraph GNN (SGNN) methods for link prediction. Based on our analysis, we propose a novel full-graph GNN called ELPH (Efficient Link Prediction with Hashing) that passes subgraph sketches as messages to approximate the key components of SGNNs without explicit subgraph construction. ELPH is provably more expressive than Message Passing GNNs (MPNNs). It outperforms existing SGNN models on many standard LP benchmarks while being orders of magnitude faster. However, it shares the common GNN limitation that it is only efficient when the dataset fits in GPU memory. Accordingly, we develop a highly scalable model, called BUDDY, which uses feature precomputation to circumvent this limitation without sacrificing predictive performance. Our experiments show that BUDDY also outperforms SGNNs on standard LP benchmarks while being highly scalable and faster than ELPH.

Neural Sheaf Diffusion: A Topological Perspective on Heterophily and Oversmoothing in GNNs

Cellular sheaves equip graphs with "geometrical" structure by assigning vector spaces and linear maps to nodes and edges. Graph Neural Networks (GNNs) implicitly assume a graph with a trivial underlying sheaf. This choice is reflected in the structure of the graph Laplacian operator, the properties of the associated diffusion equation, and the characteristics of the convolutional models that discretise this equation. In this paper, we use cellular sheaf theory to show that the underlying geometry of the graph is deeply linked with the performance of GNNs in heterophilic settings and their oversmoothing behaviour. By considering a hierarchy of increasingly general sheaves, we study how the ability of the sheaf diffusion process to achieve linear separation of the classes in the infinite time limit expands. At the same time, we prove that when the sheaf is non-trivial, discretised parametric diffusion processes have greater control than GNNs over their asymptotic behaviour. On the practical side, we study how sheaves can be learned from data. The resulting sheaf diffusion models have many desirable properties that address the limitations of classical graph diffusion equations (and corresponding GNN models) and obtain state-of-the-art results in heterophilic settings. Overall, our work provides new connections between GNNs and algebraic topology and would be of interest to both fields.

On the Unreasonable Effectiveness of Feature propagation in Learning on Graphs with Missing Node Features

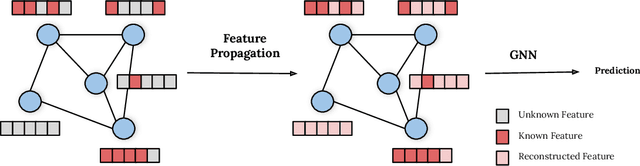
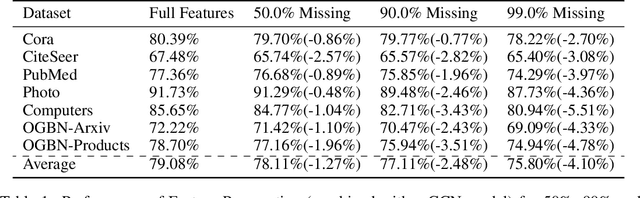
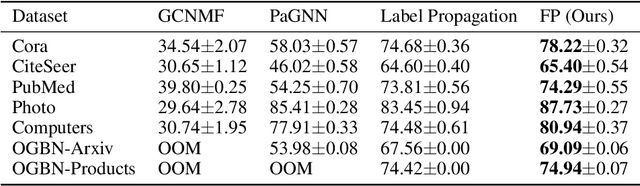
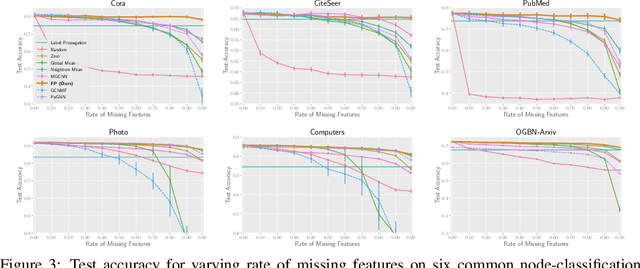
While Graph Neural Networks (GNNs) have recently become the de facto standard for modeling relational data, they impose a strong assumption on the availability of the node or edge features of the graph. In many real-world applications, however, features are only partially available; for example, in social networks, age and gender are available only for a small subset of users. We present a general approach for handling missing features in graph machine learning applications that is based on minimization of the Dirichlet energy and leads to a diffusion-type differential equation on the graph. The discretization of this equation produces a simple, fast and scalable algorithm which we call Feature Propagation. We experimentally show that the proposed approach outperforms previous methods on seven common node-classification benchmarks and can withstand surprisingly high rates of missing features: on average we observe only around 4% relative accuracy drop when 99% of the features are missing. Moreover, it takes only 10 seconds to run on a graph with $\sim$2.5M nodes and $\sim$123M edges on a single GPU.

Understanding over-squashing and bottlenecks on graphs via curvature

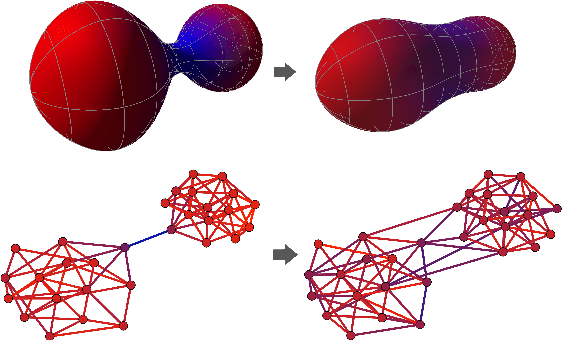
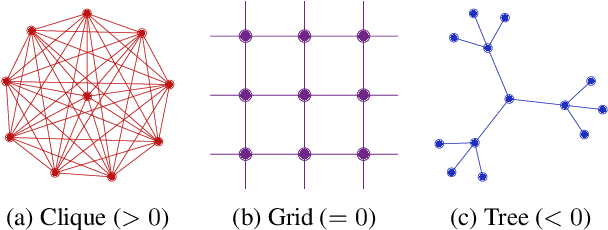
Most graph neural networks (GNNs) use the message passing paradigm, in which node features are propagated on the input graph. Recent works pointed to the distortion of information flowing from distant nodes as a factor limiting the efficiency of message passing for tasks relying on long-distance interactions. This phenomenon, referred to as 'over-squashing', has been heuristically attributed to graph bottlenecks where the number of $k$-hop neighbors grows rapidly with $k$. We provide a precise description of the over-squashing phenomenon in GNNs and analyze how it arises from bottlenecks in the graph. For this purpose, we introduce a new edge-based combinatorial curvature and prove that negatively curved edges are responsible for the over-squashing issue. We also propose and experimentally test a curvature-based graph rewiring method to alleviate the over-squashing.

Beltrami Flow and Neural Diffusion on Graphs

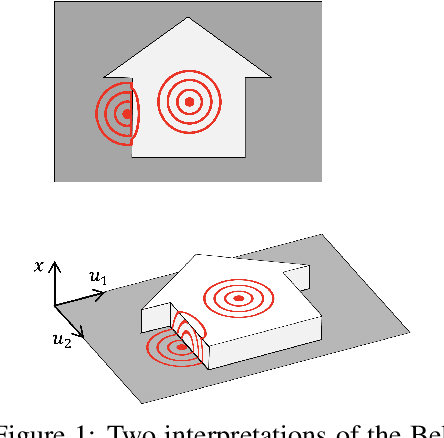
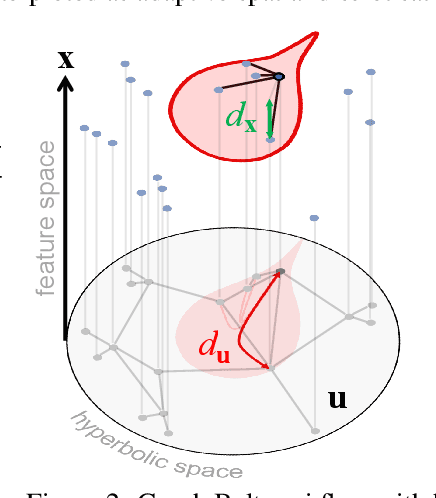
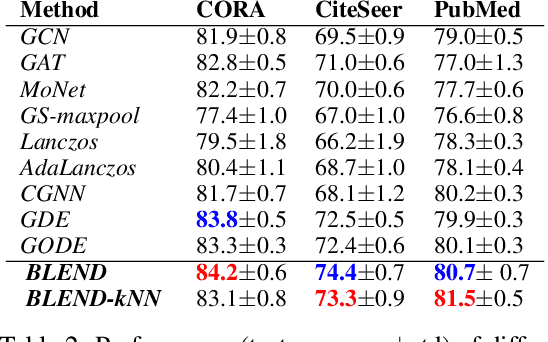
We propose a novel class of graph neural networks based on the discretised Beltrami flow, a non-Euclidean diffusion PDE. In our model, node features are supplemented with positional encodings derived from the graph topology and jointly evolved by the Beltrami flow, producing simultaneously continuous feature learning and topology evolution. The resulting model generalises many popular graph neural networks and achieves state-of-the-art results on several benchmarks.

GRAND: Graph Neural Diffusion

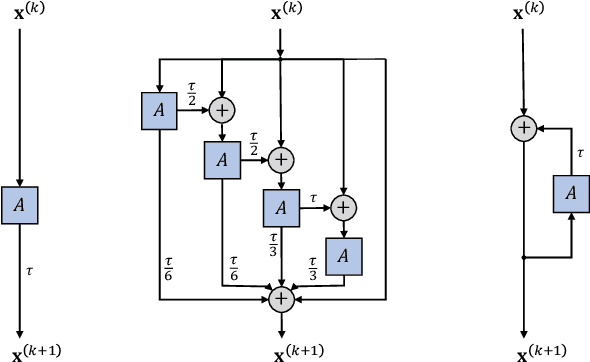
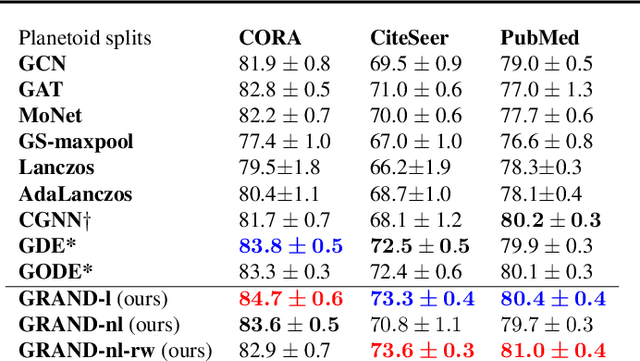
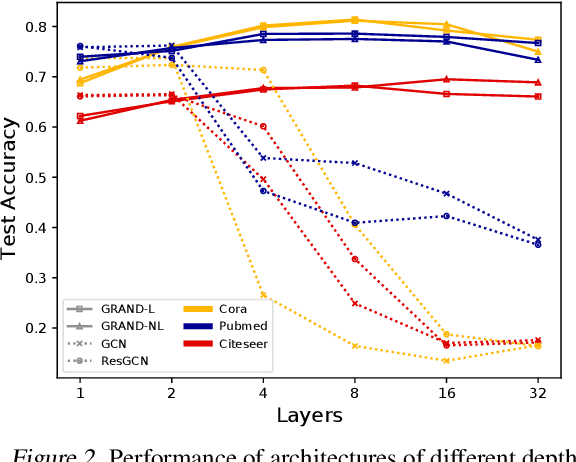
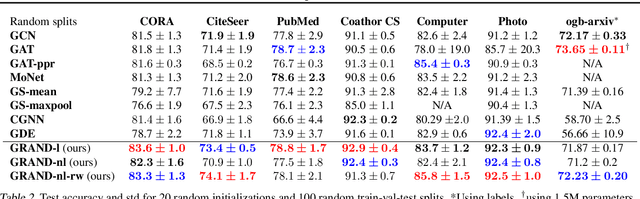
We present Graph Neural Diffusion (GRAND) that approaches deep learning on graphs as a continuous diffusion process and treats Graph Neural Networks (GNNs) as discretisations of an underlying PDE. In our model, the layer structure and topology correspond to the discretisation choices of temporal and spatial operators. Our approach allows a principled development of a broad new class of GNNs that are able to address the common plights of graph learning models such as depth, oversmoothing, and bottlenecks. Key to the success of our models are stability with respect to perturbations in the data and this is addressed for both implicit and explicit discretisation schemes. We develop linear and nonlinear versions of GRAND, which achieve competitive results on many standard graph benchmarks.

Fashion Outfit Generation for E-commerce

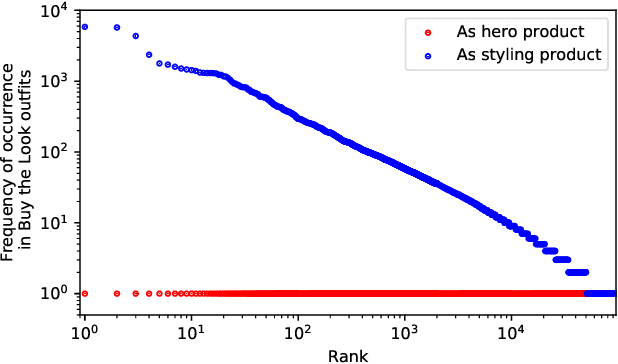
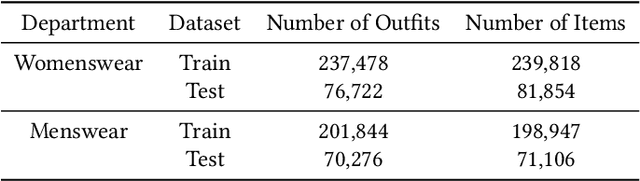
Combining items of clothing into an outfit is a major task in fashion retail. Recommending sets of items that are compatible with a particular seed item is useful for providing users with guidance and inspiration, but is currently a manual process that requires expert stylists and is therefore not scalable or easy to personalise. We use a multilayer neural network fed by visual and textual features to learn embeddings of items in a latent style space such that compatible items of different types are embedded close to one another. We train our model using the ASOS outfits dataset, which consists of a large number of outfits created by professional stylists and which we release to the research community. Our model shows strong performance in an offline outfit compatibility prediction task. We use our model to generate outfits and for the first time in this field perform an AB test, comparing our generated outfits to those produced by a baseline model which matches appropriate product types but uses no information on style. Users approved of outfits generated by our model 21% and 34% more frequently than those generated by the baseline model for womenswear and menswear respectively.

Scalable Hyperbolic Recommender Systems

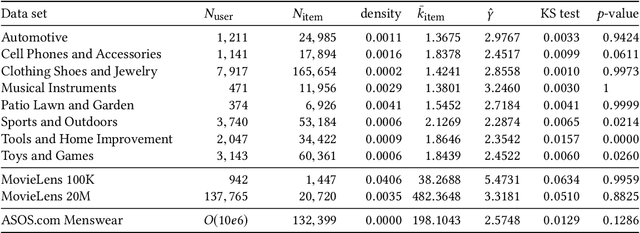
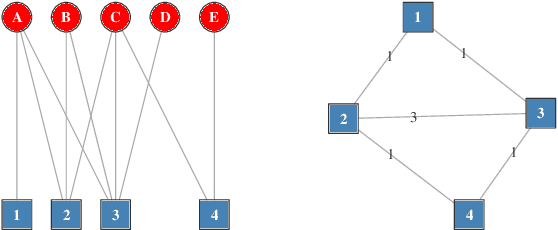
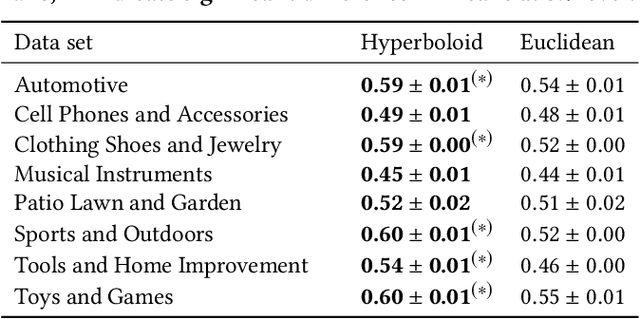
We present a large scale hyperbolic recommender system. We discuss why hyperbolic geometry is a more suitable underlying geometry for many recommendation systems and cover the fundamental milestones and insights that we have gained from its development. In doing so, we demonstrate the viability of hyperbolic geometry for recommender systems, showing that they significantly outperform Euclidean models on datasets with the properties of complex networks. Key to the success of our approach are the novel choice of underlying hyperbolic model and the use of the Einstein midpoint to define an asymmetric recommender system in hyperbolic space. These choices allow us to scale to millions of users and hundreds of thousands of items.

A Recurrent Neural Network Survival Model: Predicting Web User Return Time

The size of a website's active user base directly affects its value. Thus, it is important to monitor and influence a user's likelihood to return to a site. Essential to this is predicting when a user will return. Current state of the art approaches to solve this problem come in two flavors: (1) Recurrent Neural Network (RNN) based solutions and (2) survival analysis methods. We observe that both techniques are severely limited when applied to this problem. Survival models can only incorporate aggregate representations of users instead of automatically learning a representation directly from a raw time series of user actions. RNNs can automatically learn features, but can not be directly trained with examples of non-returning users who have no target value for their return time. We develop a novel RNN survival model that removes the limitations of the state of the art methods. We demonstrate that this model can successfully be applied to return time prediction on a large e-commerce dataset with a superior ability to discriminate between returning and non-returning users than either method applied in isolation.

Predicting Twitter User Socioeconomic Attributes with Network and Language Information

Inferring socioeconomic attributes of social media users such as occupation and income is an important problem in computational social science. Automated inference of such characteristics has applications in personalised recommender systems, targeted computational advertising and online political campaigning. While previous work has shown that language features can reliably predict socioeconomic attributes on Twitter, employing information coming from users' social networks has not yet been explored for such complex user characteristics. In this paper, we describe a method for predicting the occupational class and the income of Twitter users given information extracted from their extended networks by learning a low-dimensional vector representation of users, i.e. graph embeddings. We use this representation to train predictive models for occupational class and income. Results on two publicly available datasets show that our method consistently outperforms the state-of-the-art methods in both tasks. We also obtain further significant improvements when we combine graph embeddings with textual features, demonstrating that social network and language information are complementary.