Aurora: A Foundation Model of the Atmosphere

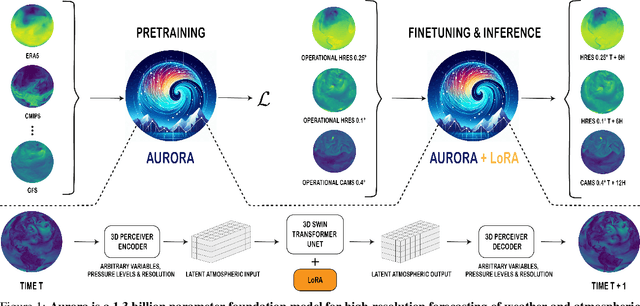
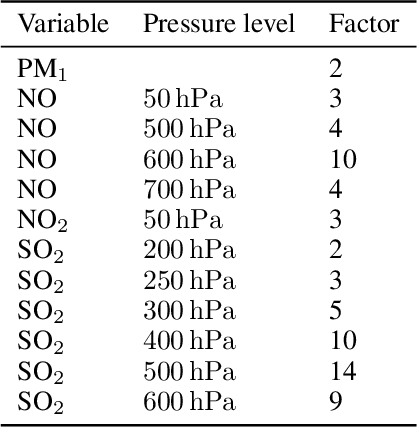
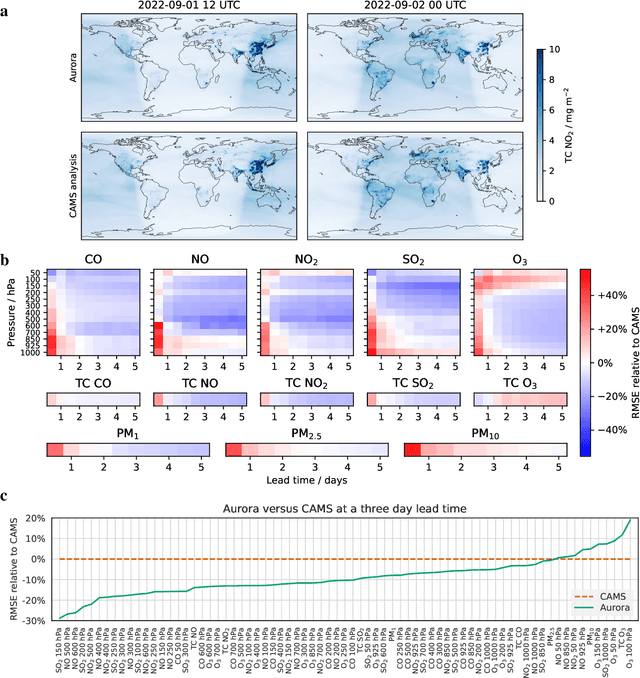
Deep learning foundation models are revolutionizing many facets of science by leveraging vast amounts of data to learn general-purpose representations that can be adapted to tackle diverse downstream tasks. Foundation models hold the promise to also transform our ability to model our planet and its subsystems by exploiting the vast expanse of Earth system data. Here we introduce Aurora, a large-scale foundation model of the atmosphere trained on over a million hours of diverse weather and climate data. Aurora leverages the strengths of the foundation modelling approach to produce operational forecasts for a wide variety of atmospheric prediction problems, including those with limited training data, heterogeneous variables, and extreme events. In under a minute, Aurora produces 5-day global air pollution predictions and 10-day high-resolution weather forecasts that outperform state-of-the-art classical simulation tools and the best specialized deep learning models. Taken together, these results indicate that foundation models can transform environmental forecasting.

Dirichlet Energy Enhancement of Graph Neural Networks by Framelet Augmentation

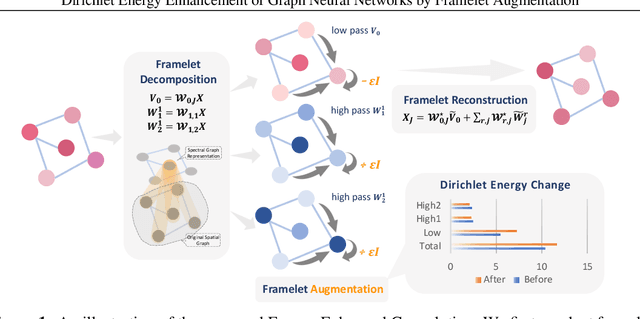
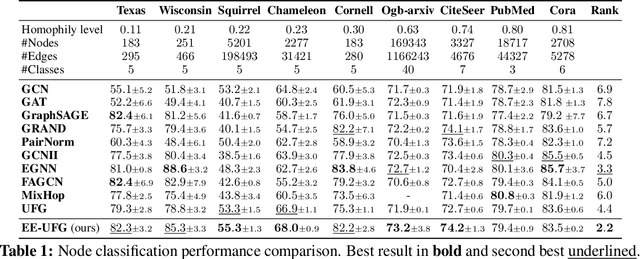
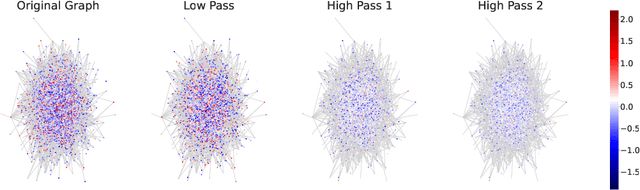
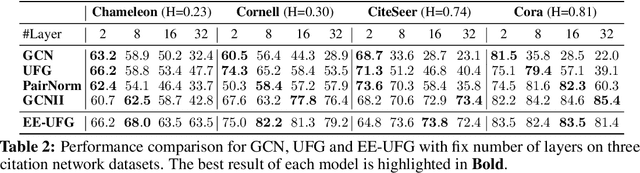
Graph convolutions have been a pivotal element in learning graph representations. However, recursively aggregating neighboring information with graph convolutions leads to indistinguishable node features in deep layers, which is known as the over-smoothing issue. The performance of graph neural networks decays fast as the number of stacked layers increases, and the Dirichlet energy associated with the graph decreases to zero as well. In this work, we introduce a framelet system into the analysis of Dirichlet energy and take a multi-scale perspective to leverage the Dirichlet energy and alleviate the over-smoothing issue. Specifically, we develop a Framelet Augmentation strategy by adjusting the update rules with positive and negative increments for low-pass and high-passes respectively. Based on that, we design the Energy Enhanced Convolution (EEConv), which is an effective and practical operation that is proved to strictly enhance Dirichlet energy. From a message-passing perspective, EEConv inherits multi-hop aggregation property from the framelet transform and takes into account all hops in the multi-scale representation, which benefits the node classification tasks over heterophilous graphs. Experiments show that deep GNNs with EEConv achieve state-of-the-art performance over various node classification datasets, especially for heterophilous graphs, while also lifting the Dirichlet energy as the network goes deeper.

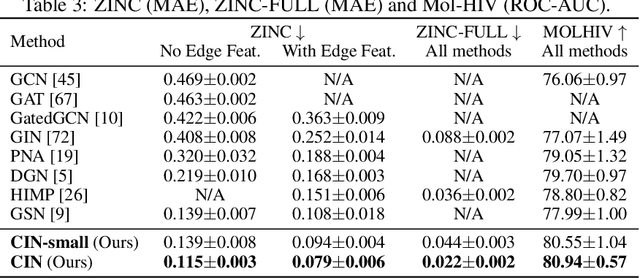
CIN++: Enhancing Topological Message Passing

Graph Neural Networks (GNNs) have demonstrated remarkable success in learning from graph-structured data. However, they face significant limitations in expressive power, struggling with long-range interactions and lacking a principled approach to modeling higher-order structures and group interactions. Cellular Isomorphism Networks (CINs) recently addressed most of these challenges with a message passing scheme based on cell complexes. Despite their advantages, CINs make use only of boundary and upper messages which do not consider a direct interaction between the rings present in the underlying complex. Accounting for these interactions might be crucial for learning representations of many real-world complex phenomena such as the dynamics of supramolecular assemblies, neural activity within the brain, and gene regulation processes. In this work, we propose CIN++, an enhancement of the topological message passing scheme introduced in CINs. Our message passing scheme accounts for the aforementioned limitations by letting the cells to receive also lower messages within each layer. By providing a more comprehensive representation of higher-order and long-range interactions, our enhanced topological message passing scheme achieves state-of-the-art results on large-scale and long-range chemistry benchmarks.

On the Expressive Power of Geometric Graph Neural Networks

The expressive power of Graph Neural Networks (GNNs) has been studied extensively through the Weisfeiler-Leman (WL) graph isomorphism test. However, standard GNNs and the WL framework are inapplicable for geometric graphs embedded in Euclidean space, such as biomolecules, materials, and other physical systems. In this work, we propose a geometric version of the WL test (GWL) for discriminating geometric graphs while respecting the underlying physical symmetries: permutations, rotation, reflection, and translation. We use GWL to characterise the expressive power of geometric GNNs that are invariant or equivariant to physical symmetries in terms of distinguishing geometric graphs. GWL unpacks how key design choices influence geometric GNN expressivity: (1) Invariant layers have limited expressivity as they cannot distinguish one-hop identical geometric graphs; (2) Equivariant layers distinguish a larger class of graphs by propagating geometric information beyond local neighbourhoods; (3) Higher order tensors and scalarisation enable maximally powerful geometric GNNs; and (4) GWL's discrimination-based perspective is equivalent to universal approximation. Synthetic experiments supplementing our results are available at https://github.com/chaitjo/geometric-gnn-dojo

Sheaf Neural Networks with Connection Laplacians

A Sheaf Neural Network (SNN) is a type of Graph Neural Network (GNN) that operates on a sheaf, an object that equips a graph with vector spaces over its nodes and edges and linear maps between these spaces. SNNs have been shown to have useful theoretical properties that help tackle issues arising from heterophily and over-smoothing. One complication intrinsic to these models is finding a good sheaf for the task to be solved. Previous works proposed two diametrically opposed approaches: manually constructing the sheaf based on domain knowledge and learning the sheaf end-to-end using gradient-based methods. However, domain knowledge is often insufficient, while learning a sheaf could lead to overfitting and significant computational overhead. In this work, we propose a novel way of computing sheaves drawing inspiration from Riemannian geometry: we leverage the manifold assumption to compute manifold-and-graph-aware orthogonal maps, which optimally align the tangent spaces of neighbouring data points. We show that this approach achieves promising results with less computational overhead when compared to previous SNN models. Overall, this work provides an interesting connection between algebraic topology and differential geometry, and we hope that it will spark future research in this direction.

Simplicial Attention Networks

Graph representation learning methods have mostly been limited to the modelling of node-wise interactions. Recently, there has been an increased interest in understanding how higher-order structures can be utilised to further enhance the learning abilities of graph neural networks (GNNs) in combinatorial spaces. Simplicial Neural Networks (SNNs) naturally model these interactions by performing message passing on simplicial complexes, higher-dimensional generalisations of graphs. Nonetheless, the computations performed by most existent SNNs are strictly tied to the combinatorial structure of the complex. Leveraging the success of attention mechanisms in structured domains, we propose Simplicial Attention Networks (SAT), a new type of simplicial network that dynamically weighs the interactions between neighbouring simplicies and can readily adapt to novel structures. Additionally, we propose a signed attention mechanism that makes SAT orientation equivariant, a desirable property for models operating on (co)chain complexes. We demonstrate that SAT outperforms existent convolutional SNNs and GNNs in two image and trajectory classification tasks.

Neural Sheaf Diffusion: A Topological Perspective on Heterophily and Oversmoothing in GNNs

Cellular sheaves equip graphs with "geometrical" structure by assigning vector spaces and linear maps to nodes and edges. Graph Neural Networks (GNNs) implicitly assume a graph with a trivial underlying sheaf. This choice is reflected in the structure of the graph Laplacian operator, the properties of the associated diffusion equation, and the characteristics of the convolutional models that discretise this equation. In this paper, we use cellular sheaf theory to show that the underlying geometry of the graph is deeply linked with the performance of GNNs in heterophilic settings and their oversmoothing behaviour. By considering a hierarchy of increasingly general sheaves, we study how the ability of the sheaf diffusion process to achieve linear separation of the classes in the infinite time limit expands. At the same time, we prove that when the sheaf is non-trivial, discretised parametric diffusion processes have greater control than GNNs over their asymptotic behaviour. On the practical side, we study how sheaves can be learned from data. The resulting sheaf diffusion models have many desirable properties that address the limitations of classical graph diffusion equations (and corresponding GNN models) and obtain state-of-the-art results in heterophilic settings. Overall, our work provides new connections between GNNs and algebraic topology and would be of interest to both fields.

Weisfeiler and Lehman Go Cellular: CW Networks

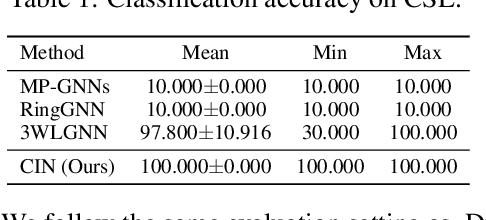
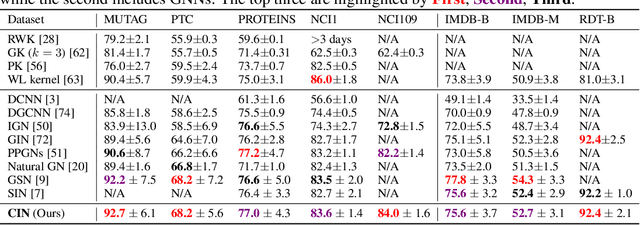
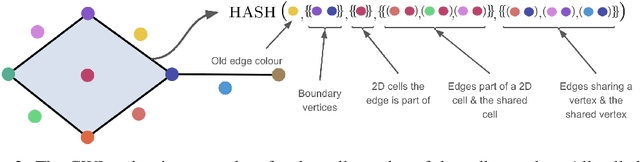
Graph Neural Networks (GNNs) are limited in their expressive power, struggle with long-range interactions and lack a principled way to model higher-order structures. These problems can be attributed to the strong coupling between the computational graph and the input graph structure. The recently proposed Message Passing Simplicial Networks naturally decouple these elements by performing message passing on the clique complex of the graph. Nevertheless, these models are severely constrained by the rigid combinatorial structure of Simplicial Complexes (SCs). In this work, we extend recent theoretical results on SCs to regular Cell Complexes, topological objects that flexibly subsume SCs and graphs. We show that this generalisation provides a powerful set of graph ``lifting'' transformations, each leading to a unique hierarchical message passing procedure. The resulting methods, which we collectively call CW Networks (CWNs), are strictly more powerful than the WL test and, in certain cases, not less powerful than the 3-WL test. In particular, we demonstrate the effectiveness of one such scheme, based on rings, when applied to molecular graph problems. The proposed architecture benefits from provably larger expressivity than commonly used GNNs, principled modelling of higher-order signals and from compressing the distances between nodes. We demonstrate that our model achieves state-of-the-art results on a variety of molecular datasets.

Neural ODE Processes

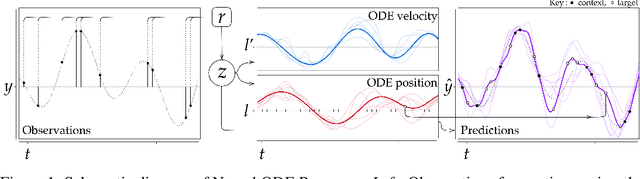
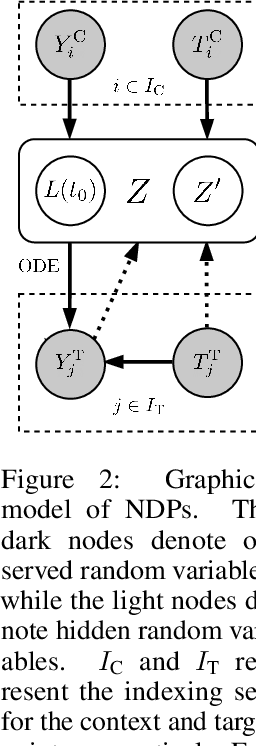
Neural Ordinary Differential Equations (NODEs) use a neural network to model the instantaneous rate of change in the state of a system. However, despite their apparent suitability for dynamics-governed time-series, NODEs present a few disadvantages. First, they are unable to adapt to incoming data-points, a fundamental requirement for real-time applications imposed by the natural direction of time. Second, time-series are often composed of a sparse set of measurements that could be explained by many possible underlying dynamics. NODEs do not capture this uncertainty. In contrast, Neural Processes (NPs) are a family of models providing uncertainty estimation and fast data-adaptation, but lack an explicit treatment of the flow of time. To address these problems, we introduce Neural ODE Processes (NDPs), a new class of stochastic processes determined by a distribution over Neural ODEs. By maintaining an adaptive data-dependent distribution over the underlying ODE, we show that our model can successfully capture the dynamics of low-dimensional systems from just a few data-points. At the same time, we demonstrate that NDPs scale up to challenging high-dimensional time-series with unknown latent dynamics such as rotating MNIST digits.

Weisfeiler and Lehman Go Topological: Message Passing Simplicial Networks

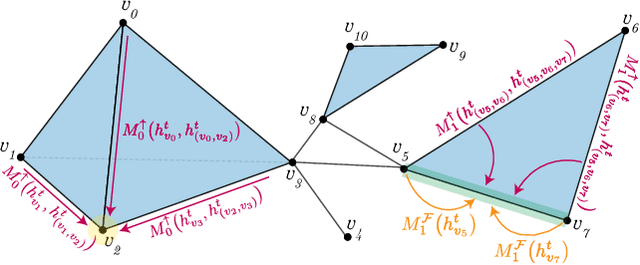
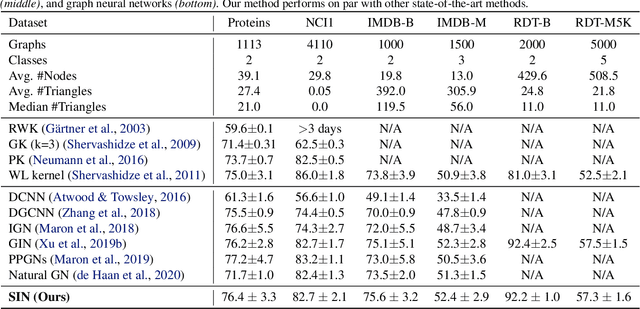
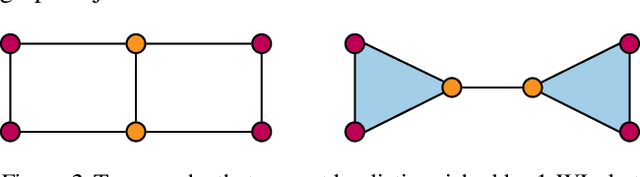
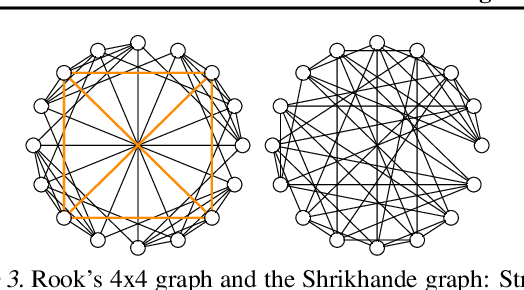
The pairwise interaction paradigm of graph machine learning has predominantly governed the modelling of relational systems. However, graphs alone cannot capture the multi-level interactions present in many complex systems and the expressive power of such schemes was proven to be limited. To overcome these limitations, we propose Message Passing Simplicial Networks (MPSNs), a class of models that perform message passing on simplicial complexes (SCs) - topological objects generalising graphs to higher dimensions. To theoretically analyse the expressivity of our model we introduce a Simplicial Weisfeiler-Lehman (SWL) colouring procedure for distinguishing non-isomorphic SCs. We relate the power of SWL to the problem of distinguishing non-isomorphic graphs and show that SWL and MPSNs are strictly more powerful than the WL test and not less powerful than the 3-WL test. We deepen the analysis by comparing our model with traditional graph neural networks with ReLU activations in terms of the number of linear regions of the functions they can represent. We empirically support our theoretical claims by showing that MPSNs can distinguish challenging strongly regular graphs for which GNNs fail and, when equipped with orientation equivariant layers, they can improve classification accuracy in oriented SCs compared to a GNN baseline. Additionally, we implement a library for message passing on simplicial complexes that we envision to release in due course.