Structure-aware generation of drug-like molecules

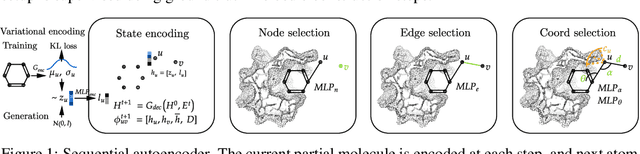
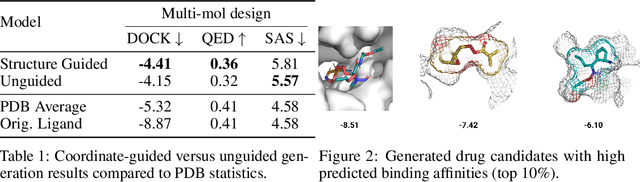
Structure-based drug design involves finding ligand molecules that exhibit structural and chemical complementarity to protein pockets. Deep generative methods have shown promise in proposing novel molecules from scratch (de-novo design), avoiding exhaustive virtual screening of chemical space. Most generative de-novo models fail to incorporate detailed ligand-protein interactions and 3D pocket structures. We propose a novel supervised model that generates molecular graphs jointly with 3D pose in a discretised molecular space. Molecules are built atom-by-atom inside pockets, guided by structural information from crystallographic data. We evaluate our model using a docking benchmark and find that guided generation improves predicted binding affinities by 8% and drug-likeness scores by 10% over the baseline. Furthermore, our model proposes molecules with binding scores exceeding some known ligands, which could be useful in future wet-lab studies.

Attentional meta-learners are polythetic classifiers

Polythetic classifications, based on shared patterns of features that need neither be universal nor constant among members of a class, are common in the natural world and greatly outnumber monothetic classifications over a set of features. We show that threshold meta-learners require an embedding dimension that is exponential in the number of features to emulate these functions. In contrast, attentional classifiers are polythetic by default and able to solve these problems with a linear embedding dimension. However, we find that in the presence of task-irrelevant features, inherent to meta-learning problems, attentional models are susceptible to misclassification. To address this challenge, we further propose a self-attention feature-selection mechanism that adaptively dilutes non-discriminative features. We demonstrate the effectiveness of our approach in meta-learning Boolean functions, and synthetic and real-world few-shot learning tasks.

Meta-learning using privileged information for dynamics

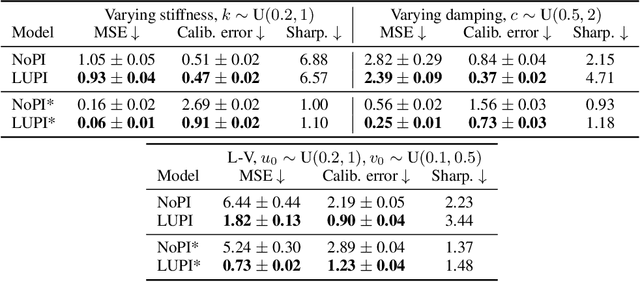
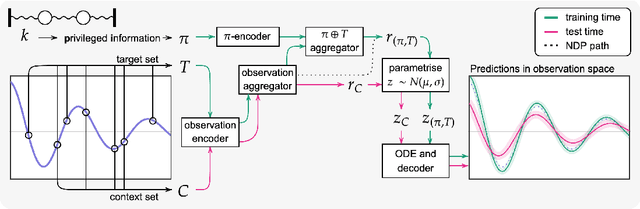
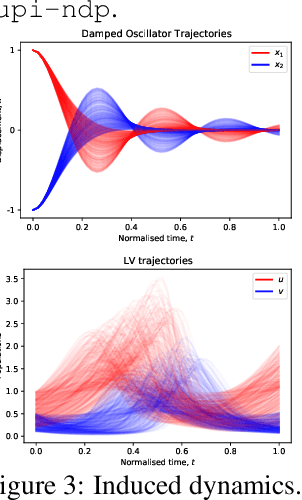
Neural ODE Processes approach the problem of meta-learning for dynamics using a latent variable model, which permits a flexible aggregation of contextual information. This flexibility is inherited from the Neural Process framework and allows the model to aggregate sets of context observations of arbitrary size into a fixed-length representation. In the physical sciences, we often have access to structured knowledge in addition to raw observations of a system, such as the value of a conserved quantity or a description of an understood component. Taking advantage of the aggregation flexibility, we extend the Neural ODE Process model to use additional information within the Learning Using Privileged Information setting, and we validate our extension with experiments showing improved accuracy and calibration on simulated dynamics tasks.

Neural ODE Processes

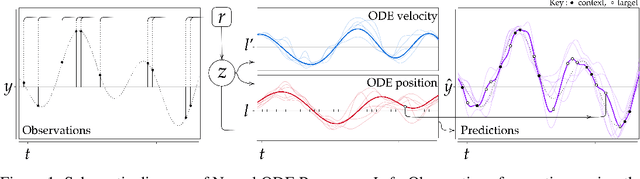
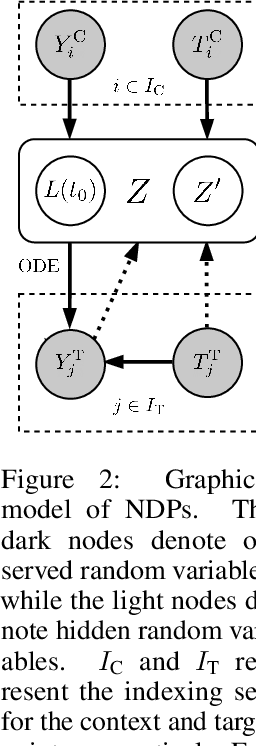
Neural Ordinary Differential Equations (NODEs) use a neural network to model the instantaneous rate of change in the state of a system. However, despite their apparent suitability for dynamics-governed time-series, NODEs present a few disadvantages. First, they are unable to adapt to incoming data-points, a fundamental requirement for real-time applications imposed by the natural direction of time. Second, time-series are often composed of a sparse set of measurements that could be explained by many possible underlying dynamics. NODEs do not capture this uncertainty. In contrast, Neural Processes (NPs) are a family of models providing uncertainty estimation and fast data-adaptation, but lack an explicit treatment of the flow of time. To address these problems, we introduce Neural ODE Processes (NDPs), a new class of stochastic processes determined by a distribution over Neural ODEs. By maintaining an adaptive data-dependent distribution over the underlying ODE, we show that our model can successfully capture the dynamics of low-dimensional systems from just a few data-points. At the same time, we demonstrate that NDPs scale up to challenging high-dimensional time-series with unknown latent dynamics such as rotating MNIST digits.

Utilising Graph Machine Learning within Drug Discovery and Development

Graph Machine Learning (GML) is receiving growing interest within the pharmaceutical and biotechnology industries for its ability to model biomolecular structures, the functional relationships between them, and integrate multi-omic datasets - amongst other data types. Herein, we present a multidisciplinary academic-industrial review of the topic within the context of drug discovery and development. After introducing key terms and modelling approaches, we move chronologically through the drug development pipeline to identify and summarise work incorporating: target identification, design of small molecules and biologics, and drug repurposing. Whilst the field is still emerging, key milestones including repurposed drugs entering in vivo studies, suggest graph machine learning will become a modelling framework of choice within biomedical machine learning.

The Role of Isomorphism Classes in Multi-Relational Datasets

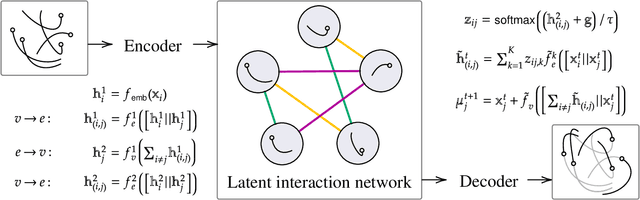
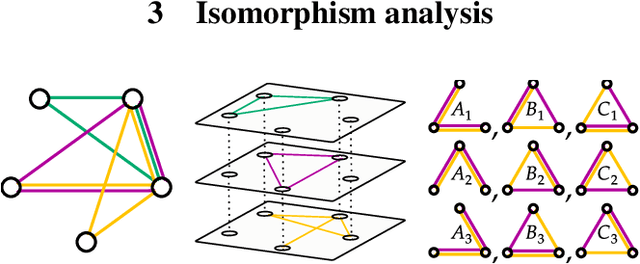
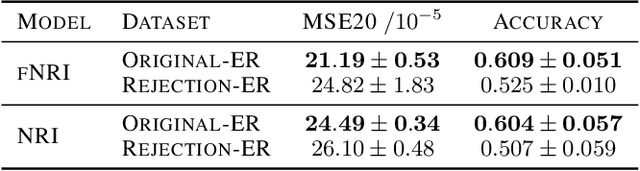
Multi-interaction systems abound in nature, from colloidal suspensions to gene regulatory circuits. These systems can produce complex dynamics and graph neural networks have been proposed as a method to extract underlying interactions and predict how systems will evolve. The current training and evaluation procedures for these models through the use of synthetic multi-relational datasets however are agnostic to interaction network isomorphism classes, which produce identical dynamics up to initial conditions. We extensively analyse how isomorphism class awareness affects these models, focusing on neural relational inference (NRI) models, which are unique in explicitly inferring interactions to predict dynamics in the unsupervised setting. Specifically, we demonstrate that isomorphism leakage overestimates performance in multi-relational inference and that sampling biases present in the multi-interaction network generation process can impair generalisation. To remedy this, we propose isomorphism-aware synthetic benchmarks for model evaluation. We use these benchmarks to test generalisation abilities and demonstrate the existence of a threshold sampling frequency of isomorphism classes for successful learning. In addition, we demonstrate that isomorphism classes can be utilised through a simple prioritisation scheme to improve model performance, stability during training and reduce training time.

Message Passing Neural Processes

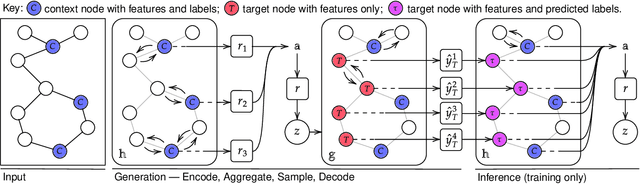
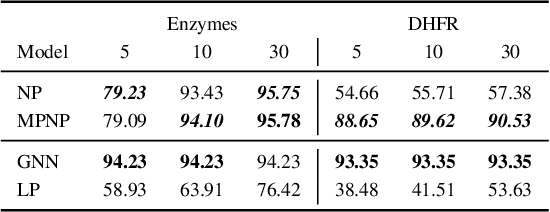
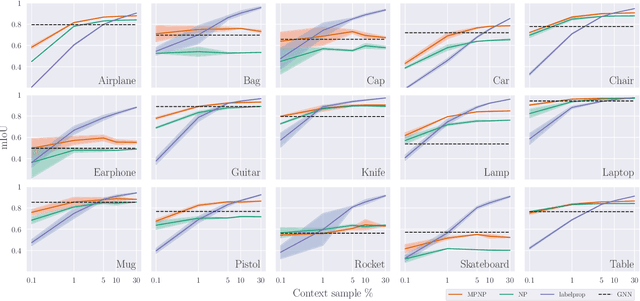
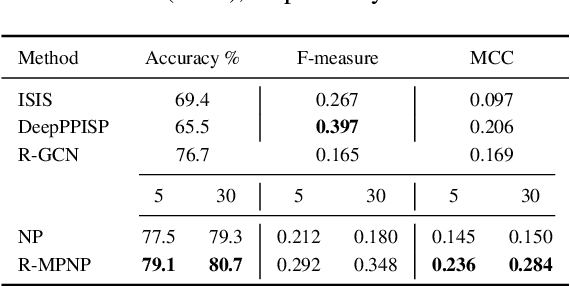
Neural Processes (NPs) are powerful and flexible models able to incorporate uncertainty when representing stochastic processes, while maintaining a linear time complexity. However, NPs produce a latent description by aggregating independent representations of context points and lack the ability to exploit relational information present in many datasets. This renders NPs ineffective in settings where the stochastic process is primarily governed by neighbourhood rules, such as cellular automata (CA), and limits performance for any task where relational information remains unused. We address this shortcoming by introducing Message Passing Neural Processes (MPNPs), the first class of NPs that explicitly makes use of relational structure within the model. Our evaluation shows that MPNPs thrive at lower sampling rates, on existing benchmarks and newly-proposed CA and Cora-Branched tasks. We further report strong generalisation over density-based CA rule-sets and significant gains in challenging arbitrary-labelling and few-shot learning setups.

Uncertainty in Neural Relational Inference Trajectory Reconstruction

Neural networks used for multi-interaction trajectory reconstruction lack the ability to estimate the uncertainty in their outputs, which would be useful to better analyse and understand the systems they model. In this paper we extend the Factorised Neural Relational Inference model to output both a mean and a standard deviation for each component of the phase space vector, which together with an appropriate loss function, can account for uncertainty. A variety of loss functions are investigated including ideas from convexification and a Bayesian treatment of the problem. We show that the physical meaning of the variables is important when considering the uncertainty and demonstrate the existence of pathological local minima that are difficult to avoid during training.

On Second Order Behaviour in Augmented Neural ODEs

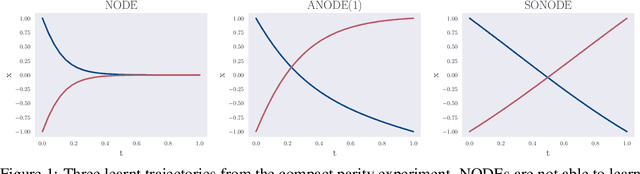
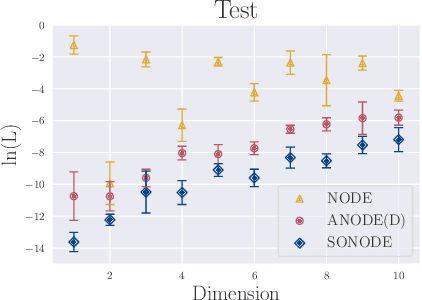
Neural Ordinary Differential Equations (NODEs) are a new class of models that transform data continuously through infinite-depth architectures. The continuous nature of NODEs has made them particularly suitable for learning the dynamics of complex physical systems. While previous work has mostly been focused on first order ODEs, the dynamics of many systems, especially in classical physics, are governed by second order laws. In this work, we take a closer look at Second Order Neural ODEs (SONODEs). We show how the adjoint sensitivity method can be extended to SONODEs and prove that an alternative first order optimisation method is computationally more efficient. Furthermore, we extend the theoretical understanding of the broader class of Augmented NODEs (ANODEs) by showing they can also learn higher order dynamics, but at the cost of interpretability. This indicates that the advantages of ANODEs go beyond the extra space offered by the augmented dimensions, as originally thought. Finally, we compare SONODEs and ANODEs on synthetic and real dynamical systems and demonstrate that the inductive biases of the former generally result in faster training and better performance.

Proximal Distilled Evolutionary Reinforcement Learning

Reinforcement Learning (RL) has recently achieved tremendous success due to the partnership with Deep Neural Networks (DNNs). Genetic Algorithms (GAs), often seen as a competing approach to RL, have run out of favour due to their inability to scale up to the DNNs required to solve the most complex environments. Contrary to this dichotomic view, in the physical world, evolution and learning are complementary processes that continuously interact. The recently proposed Evolutionary Reinforcement Learning (ERL) framework has demonstrated the capacity of the two methods to enhance each other. However, ERL has not fully addressed the scalability problem of GAs. In this paper, we argue that this problem is rooted in an unfortunate combination of a simple genetic encoding for DNNs and the use of traditional biologically-inspired variation operators. When applied to these encodings, the standard operators are destructive and cause catastrophic forgetting of the traits the networks acquired. We propose a novel algorithm called Proximal Distilled Evolutionary Reinforcement Learning (PDERL) that is characterised by a hierarchical integration between evolution and learning. The main innovation of PDERL is the use of learning-based variation operators that compensate for the simplicity of the genetic representation. Unlike the traditional operators, the ones we propose meet their functional requirements. We evaluate PDERL in five robot locomotion environments from the OpenAI gym. Our method outperforms ERL, as well as two state of the art RL algorithms, PPO and TD3, in all the environments.