Multi-State RNA Design with Geometric Multi-Graph Neural Networks

Computational RNA design has broad applications across synthetic biology and therapeutic development. Fundamental to the diverse biological functions of RNA is its conformational flexibility, enabling single sequences to adopt a variety of distinct 3D states. Currently, computational biomolecule design tasks are often posed as inverse problems, where sequences are designed based on adopting a single desired structural conformation. In this work, we propose gRNAde, a geometric RNA design pipeline that operates on sets of 3D RNA backbone structures to explicitly account for and reflect RNA conformational diversity in its designs. We demonstrate the utility of gRNAde for improving native sequence recovery over single-state approaches on a new large-scale 3D RNA design dataset, especially for multi-state and structurally diverse RNAs. Our code is available at https://github.com/chaitjo/geometric-rna-design

Attentional meta-learners are polythetic classifiers

Polythetic classifications, based on shared patterns of features that need neither be universal nor constant among members of a class, are common in the natural world and greatly outnumber monothetic classifications over a set of features. We show that threshold meta-learners require an embedding dimension that is exponential in the number of features to emulate these functions. In contrast, attentional classifiers are polythetic by default and able to solve these problems with a linear embedding dimension. However, we find that in the presence of task-irrelevant features, inherent to meta-learning problems, attentional models are susceptible to misclassification. To address this challenge, we further propose a self-attention feature-selection mechanism that adaptively dilutes non-discriminative features. We demonstrate the effectiveness of our approach in meta-learning Boolean functions, and synthetic and real-world few-shot learning tasks.

Kolmogorov Regularization for Link Prediction

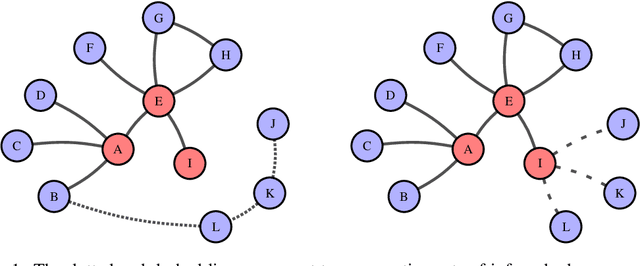
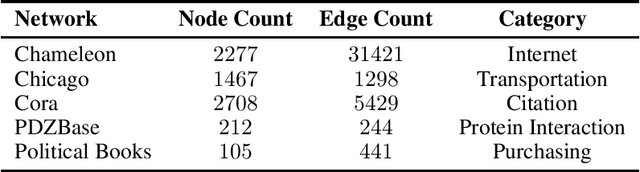
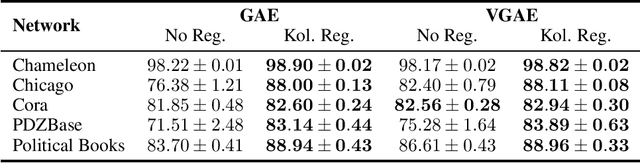
Link prediction in graphs is an important task in the fields of network science and machine learning. We propose a flexible means of regularization for link prediction based on an approximation of the Kolmogorov complexity of graphs. Informally, the Kolmogorov complexity of an object is the length of the shortest computer program that produces the object. Complex networks are often generated, in part, by simple mechanisms; for example, many citation networks and social networks are approximately scale-free and can be explained by preferential attachment. A preference for predicting graphs with simpler generating mechanisms motivates our choice of Kolmogorov complexity as a regularization term. Our method is differentiable, fast and compatible with recent advances in link prediction algorithms based on graph neural networks. We demonstrate the effectiveness of our regularization technique on a set of diverse real-world networks.