Paris D. L. Flood
Kolmogorov Regularization for Link Prediction
Jun 07, 2020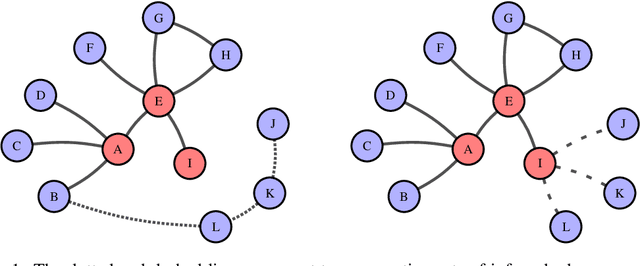
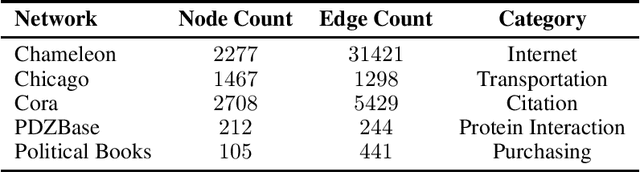

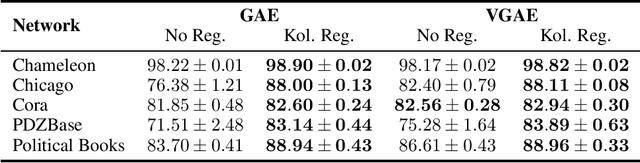
Abstract:Link prediction in graphs is an important task in the fields of network science and machine learning. We propose a flexible means of regularization for link prediction based on an approximation of the Kolmogorov complexity of graphs. Informally, the Kolmogorov complexity of an object is the length of the shortest computer program that produces the object. Complex networks are often generated, in part, by simple mechanisms; for example, many citation networks and social networks are approximately scale-free and can be explained by preferential attachment. A preference for predicting graphs with simpler generating mechanisms motivates our choice of Kolmogorov complexity as a regularization term. Our method is differentiable, fast and compatible with recent advances in link prediction algorithms based on graph neural networks. We demonstrate the effectiveness of our regularization technique on a set of diverse real-world networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge