GAUCHE: A Library for Gaussian Processes in Chemistry

We introduce GAUCHE, a library for GAUssian processes in CHEmistry. Gaussian processes have long been a cornerstone of probabilistic machine learning, affording particular advantages for uncertainty quantification and Bayesian optimisation. Extending Gaussian processes to chemical representations, however, is nontrivial, necessitating kernels defined over structured inputs such as graphs, strings and bit vectors. By defining such kernels in GAUCHE, we seek to open the door to powerful tools for uncertainty quantification and Bayesian optimisation in chemistry. Motivated by scenarios frequently encountered in experimental chemistry, we showcase applications for GAUCHE in molecular discovery and chemical reaction optimisation. The codebase is made available at https://github.com/leojklarner/gauche

Approximate Latent Force Model Inference

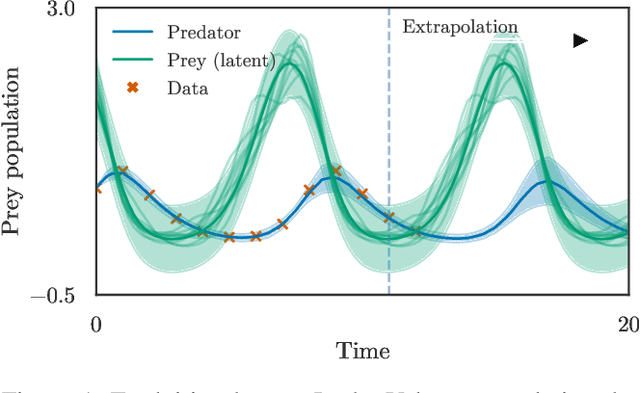
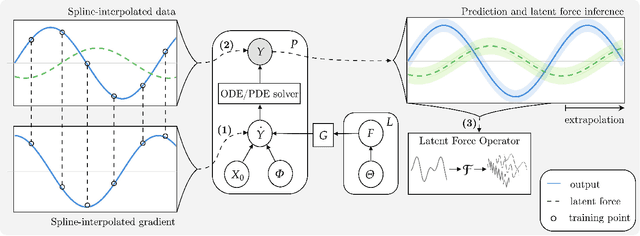
Physically-inspired latent force models offer an interpretable alternative to purely data driven tools for inference in dynamical systems. They carry the structure of differential equations and the flexibility of Gaussian processes, yielding interpretable parameters and dynamics-imposed latent functions. However, the existing inference techniques associated with these models rely on the exact computation of posterior kernel terms which are seldom available in analytical form. Most applications relevant to practitioners, such as Hill equations or diffusion equations, are hence intractable. In this paper, we overcome these computational problems by proposing a variational solution to a general class of non-linear and parabolic partial differential equation latent force models. Further, we show that a neural operator approach can scale our model to thousands of instances, enabling fast, distributed computation. We demonstrate the efficacy and flexibility of our framework by achieving competitive performance on several tasks where the kernels are of varying degrees of tractability.

Modular Neural Ordinary Differential Equations

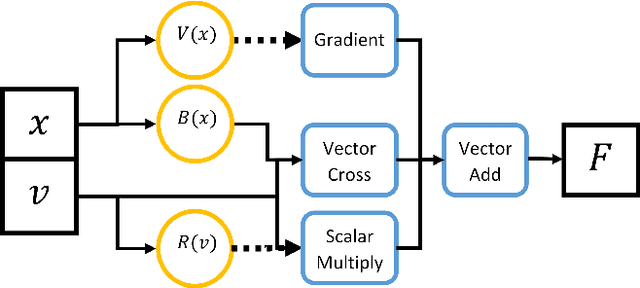
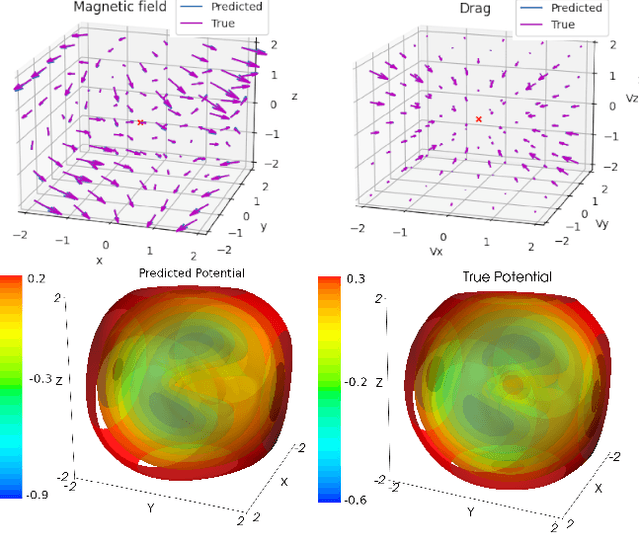
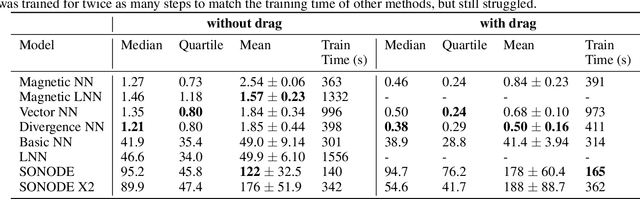
The laws of physics have been written in the language of dif-ferential equations for centuries. Neural Ordinary Differen-tial Equations (NODEs) are a new machine learning architecture which allows these differential equations to be learned from a dataset. These have been applied to classical dynamics simulations in the form of Lagrangian Neural Net-works (LNNs) and Second Order Neural Differential Equations (SONODEs). However, they either cannot represent the most general equations of motion or lack interpretability. In this paper, we propose Modular Neural ODEs, where each force component is learned with separate modules. We show how physical priors can be easily incorporated into these models. Through a number of experiments, we demonstrate these result in better performance, are more interpretable, and add flexibility due to their modularity.

Meta-learning using privileged information for dynamics

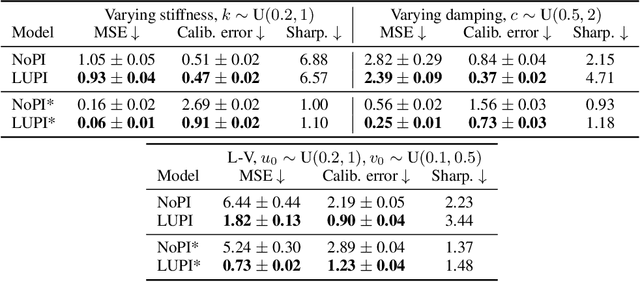
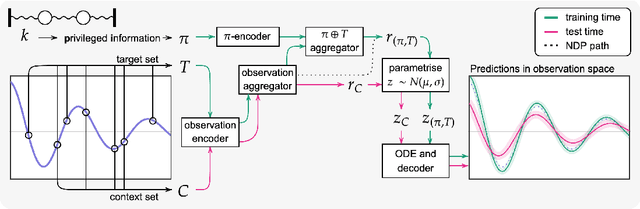
Neural ODE Processes approach the problem of meta-learning for dynamics using a latent variable model, which permits a flexible aggregation of contextual information. This flexibility is inherited from the Neural Process framework and allows the model to aggregate sets of context observations of arbitrary size into a fixed-length representation. In the physical sciences, we often have access to structured knowledge in addition to raw observations of a system, such as the value of a conserved quantity or a description of an understood component. Taking advantage of the aggregation flexibility, we extend the Neural ODE Process model to use additional information within the Learning Using Privileged Information setting, and we validate our extension with experiments showing improved accuracy and calibration on simulated dynamics tasks.

Neural ODE Processes

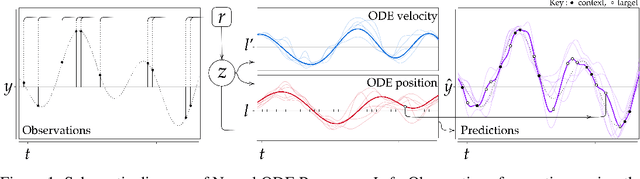
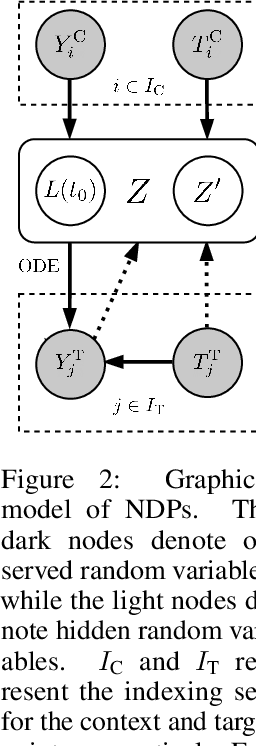
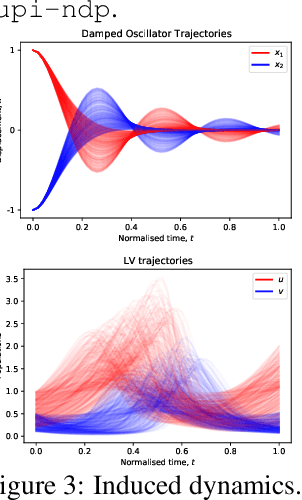
Neural Ordinary Differential Equations (NODEs) use a neural network to model the instantaneous rate of change in the state of a system. However, despite their apparent suitability for dynamics-governed time-series, NODEs present a few disadvantages. First, they are unable to adapt to incoming data-points, a fundamental requirement for real-time applications imposed by the natural direction of time. Second, time-series are often composed of a sparse set of measurements that could be explained by many possible underlying dynamics. NODEs do not capture this uncertainty. In contrast, Neural Processes (NPs) are a family of models providing uncertainty estimation and fast data-adaptation, but lack an explicit treatment of the flow of time. To address these problems, we introduce Neural ODE Processes (NDPs), a new class of stochastic processes determined by a distribution over Neural ODEs. By maintaining an adaptive data-dependent distribution over the underlying ODE, we show that our model can successfully capture the dynamics of low-dimensional systems from just a few data-points. At the same time, we demonstrate that NDPs scale up to challenging high-dimensional time-series with unknown latent dynamics such as rotating MNIST digits.

Gene Regulatory Network Inference with Latent Force Models

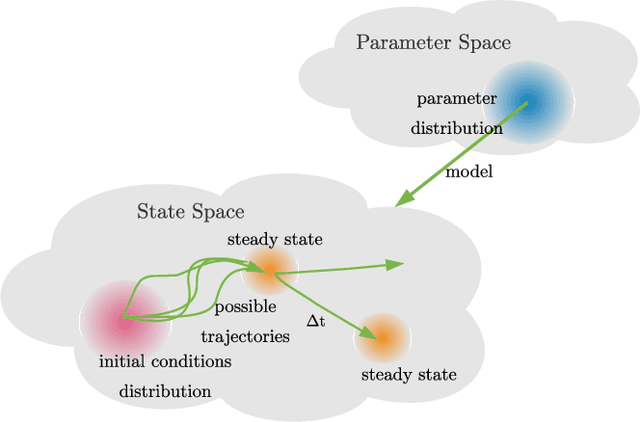
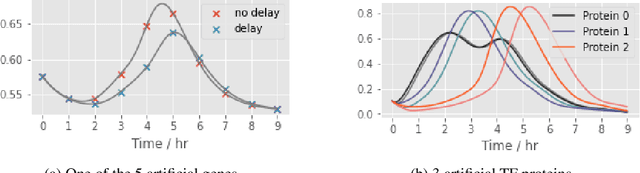
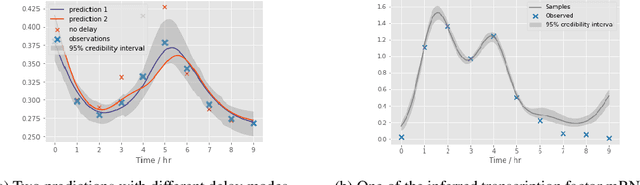
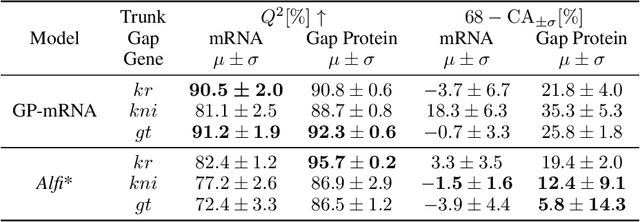
Delays in protein synthesis cause a confounding effect when constructing Gene Regulatory Networks (GRNs) from RNA-sequencing time-series data. Accurate GRNs can be very insightful when modelling development, disease pathways, and drug side-effects. We present a model which incorporates translation delays by combining mechanistic equations and Bayesian approaches to fit to experimental data. This enables greater biological interpretability, and the use of Gaussian processes enables non-linear expressivity through kernels as well as naturally accounting for biological variation.