MarkerMap: nonlinear marker selection for single-cell studies

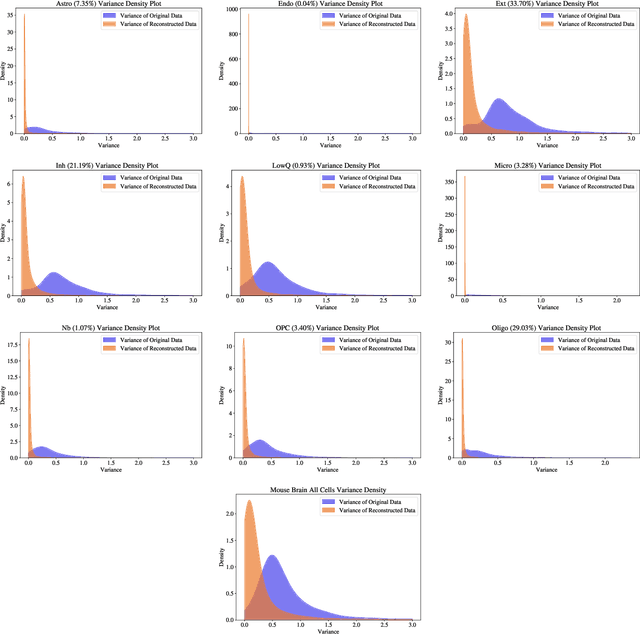
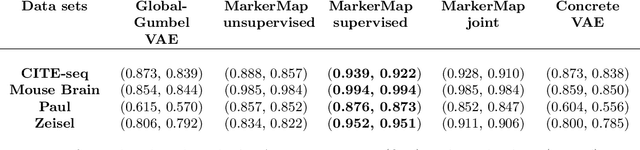
Single-cell RNA-seq data allow the quantification of cell type differences across a growing set of biological contexts. However, pinpointing a small subset of genomic features explaining this variability can be ill-defined and computationally intractable. Here we introduce MarkerMap, a generative model for selecting minimal gene sets which are maximally informative of cell type origin and enable whole transcriptome reconstruction. MarkerMap provides a scalable framework for both supervised marker selection, aimed at identifying specific cell type populations, and unsupervised marker selection, aimed at gene expression imputation and reconstruction. We benchmark MarkerMap's competitive performance against previously published approaches on real single cell gene expression data sets. MarkerMap is available as a pip installable package, as a community resource aimed at developing explainable machine learning techniques for enhancing interpretability in single-cell studies.

Dimensionless machine learning: Imposing exact units equivariance

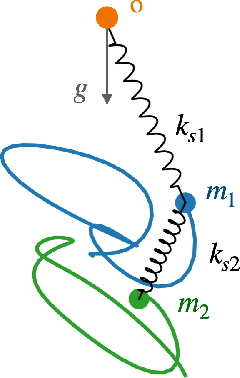
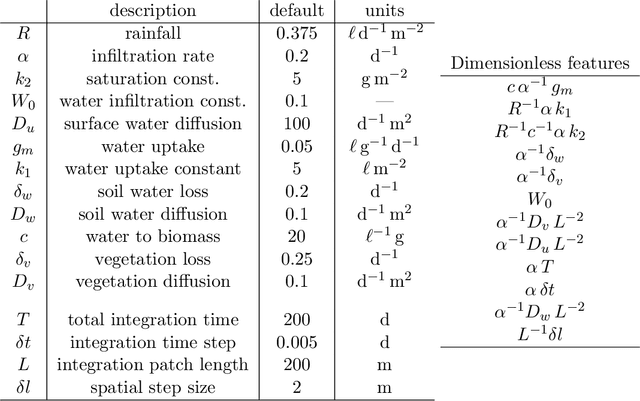
Units equivariance is the exact symmetry that follows from the requirement that relationships among measured quantities of physics relevance must obey self-consistent dimensional scalings. Here, we employ dimensional analysis and ideas from equivariant machine learning to provide a two stage learning procedure for units-equivariant machine learning. For a given learning task, we first construct a dimensionless version of its inputs using classic results from dimensional analysis, and then perform inference in the dimensionless space. Our approach can be used to impose units equivariance across a broad range of machine learning methods which are equivariant to rotations and other groups. We discuss the in-sample and out-of-sample prediction accuracy gains one can obtain in contexts like symbolic regression and emulation, where symmetry is important. We illustrate our approach with simple numerical examples involving dynamical systems in physics and ecology.

Approximate Latent Force Model Inference

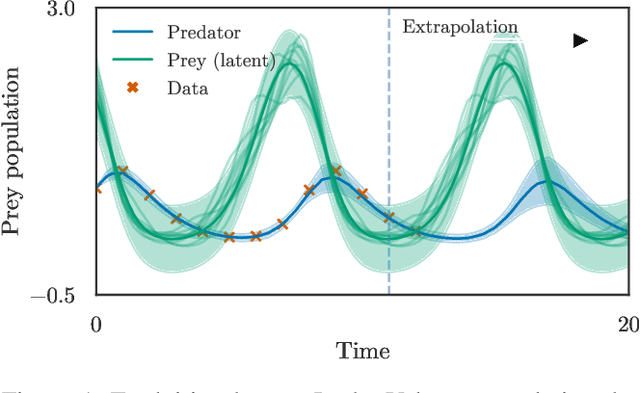
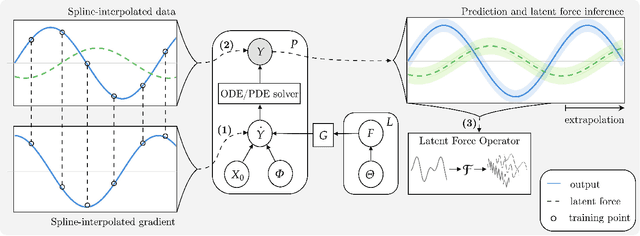
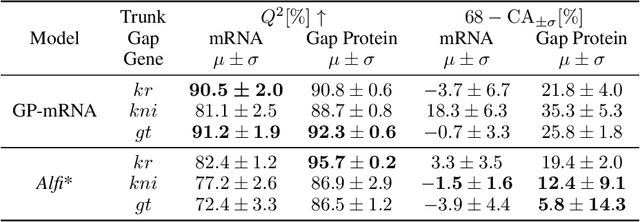
Physically-inspired latent force models offer an interpretable alternative to purely data driven tools for inference in dynamical systems. They carry the structure of differential equations and the flexibility of Gaussian processes, yielding interpretable parameters and dynamics-imposed latent functions. However, the existing inference techniques associated with these models rely on the exact computation of posterior kernel terms which are seldom available in analytical form. Most applications relevant to practitioners, such as Hill equations or diffusion equations, are hence intractable. In this paper, we overcome these computational problems by proposing a variational solution to a general class of non-linear and parabolic partial differential equation latent force models. Further, we show that a neural operator approach can scale our model to thousands of instances, enabling fast, distributed computation. We demonstrate the efficacy and flexibility of our framework by achieving competitive performance on several tasks where the kernels are of varying degrees of tractability.

Patient-Specific Effects of Medication Using Latent Force Models with Gaussian Processes

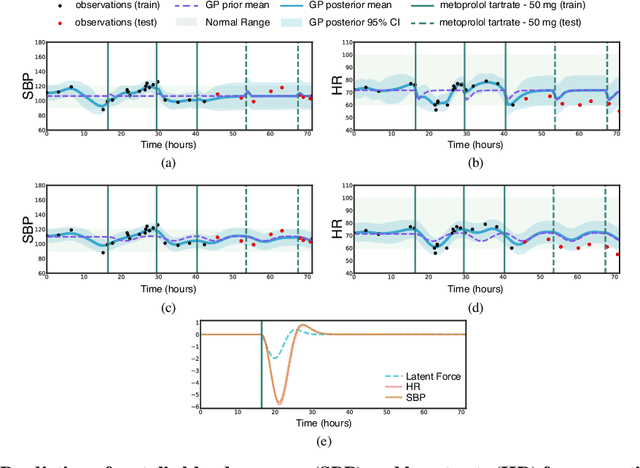
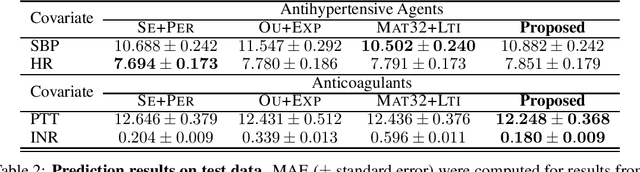
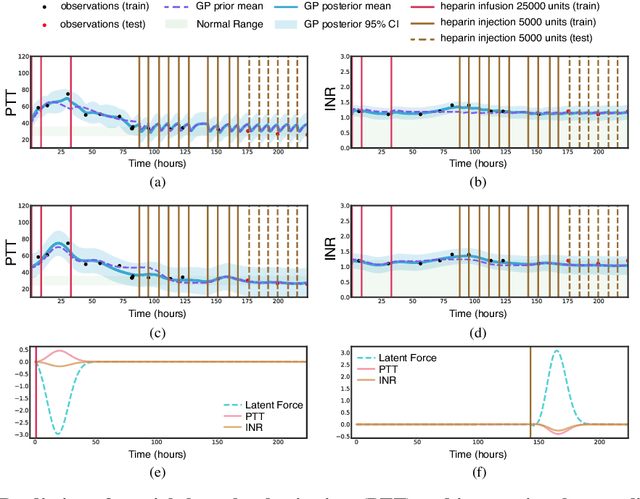
Multi-output Gaussian processes (GPs) are a flexible Bayesian nonparametric framework that has proven useful in jointly modeling the physiological states of patients in medical time series data. However, capturing the short-term effects of drugs and therapeutic interventions on patient physiological state remains challenging. We propose a novel approach that models the effect of interventions as a hybrid Gaussian process composed of a GP capturing patient physiology convolved with a latent force model capturing effects of treatments on specific physiological features. This convolution of a multi-output GP with a GP including a causal time-marked kernel leads to a well-characterized model of the patients' physiological state responding to interventions. We show that our model leads to analytically tractable cross-covariance functions, allowing scalable inference. Our hierarchical model includes estimates of patient-specific effects but allows sharing of support across patients. Our approach achieves competitive predictive performance on challenging hospital data, where we recover patient-specific response to the administration of three common drugs: one antihypertensive drug and two anticoagulants.

Sequential Gaussian Processes for Online Learning of Nonstationary Functions

Many machine learning problems can be framed in the context of estimating functions, and often these are time-dependent functions that are estimated in real-time as observations arrive. Gaussian processes (GPs) are an attractive choice for modeling real-valued nonlinear functions due to their flexibility and uncertainty quantification. However, the typical GP regression model suffers from several drawbacks: i) Conventional GP inference scales $O(N^{3})$ with respect to the number of observations; ii) updating a GP model sequentially is not trivial; and iii) covariance kernels often enforce stationarity constraints on the function, while GPs with non-stationary covariance kernels are often intractable to use in practice. To overcome these issues, we propose an online sequential Monte Carlo algorithm to fit mixtures of GPs that capture non-stationary behavior while allowing for fast, distributed inference. By formulating hyperparameter optimization as a multi-armed bandit problem, we accelerate mixing for real time inference. Our approach empirically improves performance over state-of-the-art methods for online GP estimation in the context of prediction for simulated non-stationary data and hospital time series data.

Sparse Multi-Output Gaussian Processes for Medical Time Series Prediction

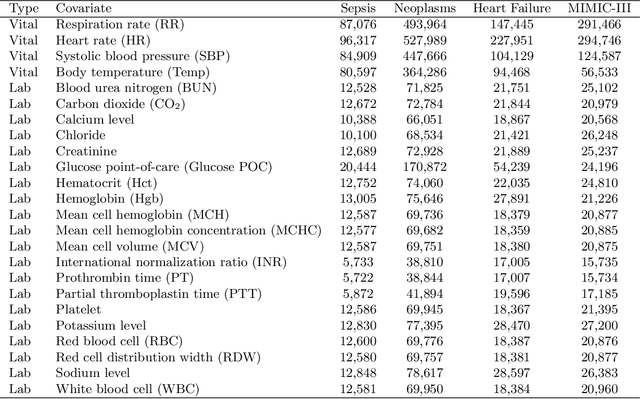
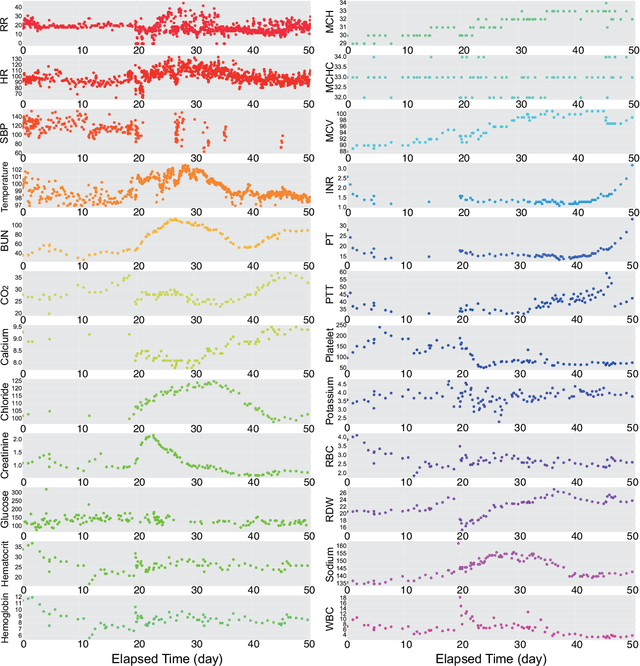
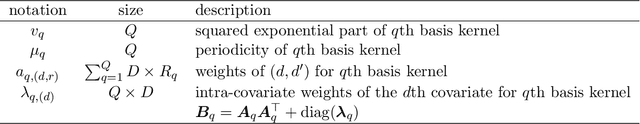
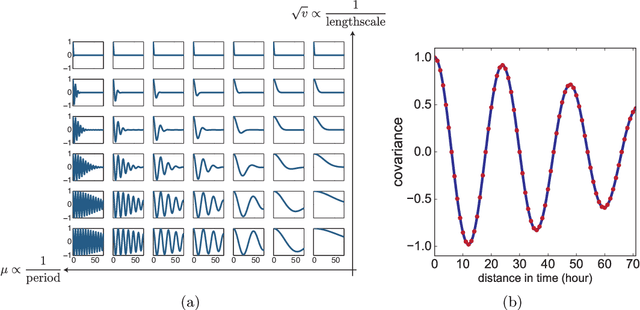
In the scenario of real-time monitoring of hospital patients, high-quality inference of patients' health status using all information available from clinical covariates and lab tests is essential to enable successful medical interventions and improve patient outcomes. Developing a computational framework that can learn from observational large-scale electronic health records (EHRs) and make accurate real-time predictions is a critical step. In this work, we develop and explore a Bayesian nonparametric model based on Gaussian process (GP) regression for hospital patient monitoring. We propose MedGP, a statistical framework that incorporates 24 clinical and lab covariates and supports a rich reference data set from which relationships between observed covariates may be inferred and exploited for high-quality inference of patient state over time. To do this, we develop a highly structured sparse GP kernel to enable tractable computation over tens of thousands of time points while estimating correlations among clinical covariates, patients, and periodicity in patient observations. MedGP has a number of benefits over current methods, including (i) not requiring an alignment of the time series data, (ii) quantifying confidence regions in the predictions, (iii) exploiting a vast and rich database of patients, and (iv) inferring interpretable relationships among clinical covariates. We evaluate and compare results from MedGP on the task of online prediction for three patient subgroups from two medical data sets across 8,043 patients. We found MedGP improves online prediction over baseline methods for nearly all covariates across different disease subgroups and studies. The publicly available code is at https://github.com/bee-hive/MedGP.

PG-TS: Improved Thompson Sampling for Logistic Contextual Bandits

We address the problem of regret minimization in logistic contextual bandits, where a learner decides among sequential actions or arms given their respective contexts to maximize binary rewards. Using a fast inference procedure with Polya-Gamma distributed augmentation variables, we propose an improved version of Thompson Sampling, a Bayesian formulation of contextual bandits with near-optimal performance. Our approach, Polya-Gamma augmented Thompson Sampling (PG-TS), achieves state-of-the-art performance on simulated and real data. PG-TS explores the action space efficiently and exploits high-reward arms, quickly converging to solutions of low regret. Its explicit estimation of the posterior distribution of the context feature covariance leads to substantial empirical gains over approximate approaches. PG-TS is the first approach to demonstrate the benefits of Polya-Gamma augmentation in bandits and to propose an efficient Gibbs sampler for approximating the analytically unsolvable integral of logistic contextual bandits.