Learning functions on symmetric matrices and point clouds via lightweight invariant features

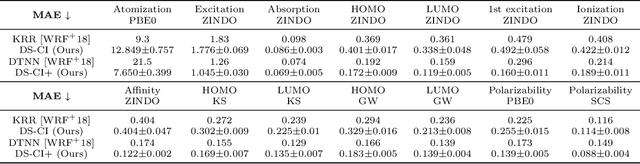
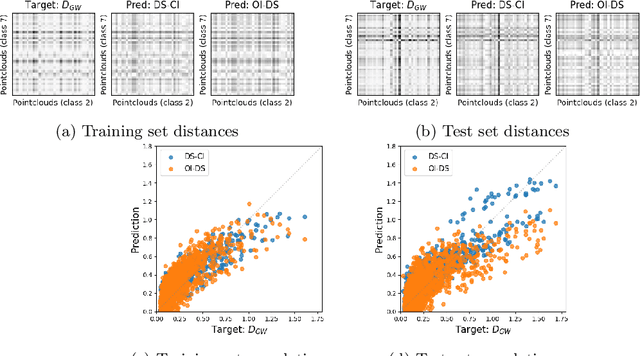
In this work, we present a mathematical formulation for machine learning of (1) functions on symmetric matrices that are invariant with respect to the action of permutations by conjugation, and (2) functions on point clouds that are invariant with respect to rotations, reflections, and permutations of the points. To achieve this, we construct $O(n^2)$ invariant features derived from generators for the field of rational functions on $n\times n$ symmetric matrices that are invariant under joint permutations of rows and columns. We show that these invariant features can separate all distinct orbits of symmetric matrices except for a measure zero set; such features can be used to universally approximate invariant functions on almost all weighted graphs. For point clouds in a fixed dimension, we prove that the number of invariant features can be reduced, generically without losing expressivity, to $O(n)$, where $n$ is the number of points. We combine these invariant features with DeepSets to learn functions on symmetric matrices and point clouds with varying sizes. We empirically demonstrate the feasibility of our approach on molecule property regression and point cloud distance prediction.

GeometricImageNet: Extending convolutional neural networks to vector and tensor images

Convolutional neural networks and their ilk have been very successful for many learning tasks involving images. These methods assume that the input is a scalar image representing the intensity in each pixel, possibly in multiple channels for color images. In natural-science domains however, image-like data sets might have vectors (velocity, say), tensors (polarization, say), pseudovectors (magnetic field, say), or other geometric objects in each pixel. Treating the components of these objects as independent channels in a CNN neglects their structure entirely. Our formulation -- the GeometricImageNet -- combines a geometric generalization of convolution with outer products, tensor index contractions, and tensor index permutations to construct geometric-image functions of geometric images that use and benefit from the tensor structure. The framework permits, with a very simple adjustment, restriction to function spaces that are exactly equivariant to translations, discrete rotations, and reflections. We use representation theory to quantify the dimension of the space of equivariant polynomial functions on 2-dimensional vector images. We give partial results on the expressivity of GeometricImageNet on small images. In numerical experiments, we find that GeometricImageNet has good generalization for a small simulated physics system, even when trained with a small training set. We expect this tool will be valuable for scientific and engineering machine learning, for example in cosmology or ocean dynamics.

Equivariant maps from invariant functions

In equivariant machine learning the idea is to restrict the learning to a hypothesis class where all the functions are equivariant with respect to some group action. Irreducible representations or invariant theory are typically used to parameterize the space of such functions. In this note, we explicate a general procedure, attributed to Malgrange, to express all polynomial maps between linear spaces that are equivariant with respect to the action of a group $G$, given a characterization of the invariant polynomials on a bigger space. The method also parametrizes smooth equivariant maps in the case that $G$ is a compact Lie group.

Dimensionless machine learning: Imposing exact units equivariance

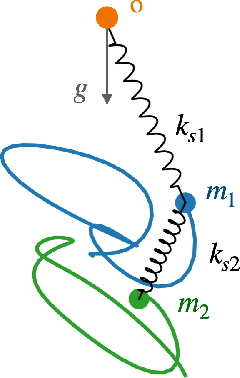
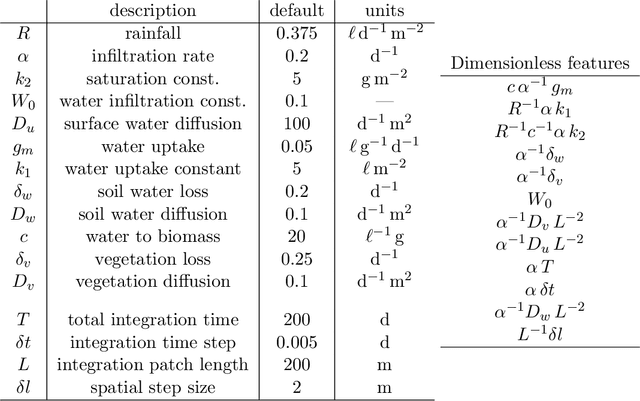
Units equivariance is the exact symmetry that follows from the requirement that relationships among measured quantities of physics relevance must obey self-consistent dimensional scalings. Here, we employ dimensional analysis and ideas from equivariant machine learning to provide a two stage learning procedure for units-equivariant machine learning. For a given learning task, we first construct a dimensionless version of its inputs using classic results from dimensional analysis, and then perform inference in the dimensionless space. Our approach can be used to impose units equivariance across a broad range of machine learning methods which are equivariant to rotations and other groups. We discuss the in-sample and out-of-sample prediction accuracy gains one can obtain in contexts like symbolic regression and emulation, where symmetry is important. We illustrate our approach with simple numerical examples involving dynamical systems in physics and ecology.

Scalars are universal: Gauge-equivariant machine learning, structured like classical physics

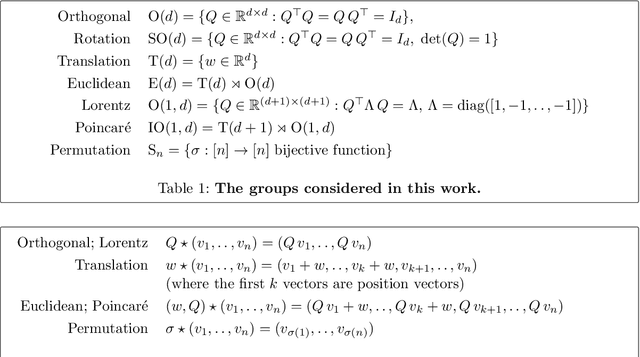
There has been enormous progress in the last few years in designing conceivable (though not always practical) neural networks that respect the gauge symmetries -- or coordinate freedom -- of physical law. Some of these frameworks make use of irreducible representations, some make use of higher order tensor objects, and some apply symmetry-enforcing constraints. Different physical laws obey different combinations of fundamental symmetries, but a large fraction (possibly all) of classical physics is equivariant to translation, rotation, reflection (parity), boost (relativity), and permutations. Here we show that it is simple to parameterize universally approximating polynomial functions that are equivariant under these symmetries, or under the Euclidean, Lorentz, and Poincar\'e groups, at any dimensionality $d$. The key observation is that nonlinear O($d$)-equivariant (and related-group-equivariant) functions can be expressed in terms of a lightweight collection of scalars -- scalar products and scalar contractions of the scalar, vector, and tensor inputs. These results demonstrate theoretically that gauge-invariant deep learning models for classical physics with good scaling for large problems are feasible right now.