Learning functions on symmetric matrices and point clouds via lightweight invariant features
Paper and Code
May 15, 2024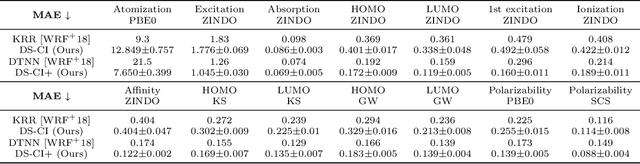
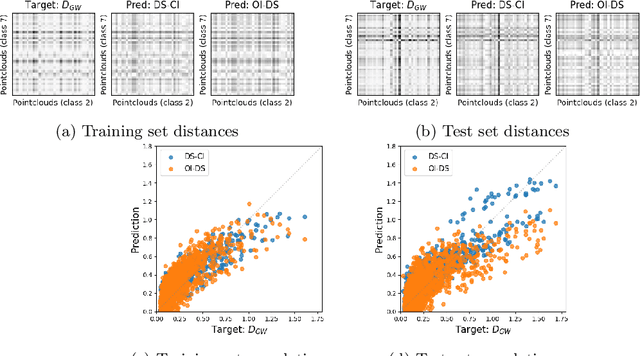
In this work, we present a mathematical formulation for machine learning of (1) functions on symmetric matrices that are invariant with respect to the action of permutations by conjugation, and (2) functions on point clouds that are invariant with respect to rotations, reflections, and permutations of the points. To achieve this, we construct $O(n^2)$ invariant features derived from generators for the field of rational functions on $n\times n$ symmetric matrices that are invariant under joint permutations of rows and columns. We show that these invariant features can separate all distinct orbits of symmetric matrices except for a measure zero set; such features can be used to universally approximate invariant functions on almost all weighted graphs. For point clouds in a fixed dimension, we prove that the number of invariant features can be reduced, generically without losing expressivity, to $O(n)$, where $n$ is the number of points. We combine these invariant features with DeepSets to learn functions on symmetric matrices and point clouds with varying sizes. We empirically demonstrate the feasibility of our approach on molecule property regression and point cloud distance prediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge