Group Averaging for Physics Applications: Accuracy Improvements at Zero Training Cost

Many machine learning tasks in the natural sciences are precisely equivariant to particular symmetries. Nonetheless, equivariant methods are often not employed, perhaps because training is perceived to be challenging, or the symmetry is expected to be learned, or equivariant implementations are seen as hard to build. Group averaging is an available technique for these situations. It happens at test time; it can make any trained model precisely equivariant at a (often small) cost proportional to the size of the group; it places no requirements on model structure or training. It is known that, under mild conditions, the group-averaged model will have a provably better prediction accuracy than the original model. Here we show that an inexpensive group averaging can improve accuracy in practice. We take well-established benchmark machine learning models of differential equations in which certain symmetries ought to be obeyed. At evaluation time, we average the models over a small group of symmetries. Our experiments show that this procedure always decreases the average evaluation loss, with improvements of up to 37\% in terms of the VRMSE. The averaging produces visually better predictions for continuous dynamics. This short paper shows that, under certain common circumstances, there are no disadvantages to imposing exact symmetries; the ML4PS community should consider group averaging as a cheap and simple way to improve model accuracy.

On Transferring Transferability: Towards a Theory for Size Generalization

Many modern learning tasks require models that can take inputs of varying sizes. Consequently, dimension-independent architectures have been proposed for domains where the inputs are graphs, sets, and point clouds. Recent work on graph neural networks has explored whether a model trained on low-dimensional data can transfer its performance to higher-dimensional inputs. We extend this body of work by introducing a general framework for transferability across dimensions. We show that transferability corresponds precisely to continuity in a limit space formed by identifying small problem instances with equivalent large ones. This identification is driven by the data and the learning task. We instantiate our framework on existing architectures, and implement the necessary changes to ensure their transferability. Finally, we provide design principles for designing new transferable models. Numerical experiments support our findings.

Towards Coordinate- and Dimension-Agnostic Machine Learning for Partial Differential Equations

The machine learning methods for data-driven identification of partial differential equations (PDEs) are typically defined for a given number of spatial dimensions and a choice of coordinates the data have been collected in. This dependence prevents the learned evolution equation from generalizing to other spaces. In this work, we reformulate the problem in terms of coordinate- and dimension-independent representations, paving the way toward what we call ``spatially liberated" PDE learning. To this end, we employ a machine learning approach to predict the evolution of scalar field systems expressed in the formalism of exterior calculus, which is coordinate-free and immediately generalizes to arbitrary dimensions by construction. We demonstrate the performance of this approach in the FitzHugh-Nagumo and Barkley reaction-diffusion models, as well as the Patlak-Keller-Segel model informed by in-situ chemotactic bacteria observations. We provide extensive numerical experiments that demonstrate that our approach allows for seamless transitions across various spatial contexts. We show that the field dynamics learned in one space can be used to make accurate predictions in other spaces with different dimensions, coordinate systems, boundary conditions, and curvatures.

Graph neural networks and non-commuting operators

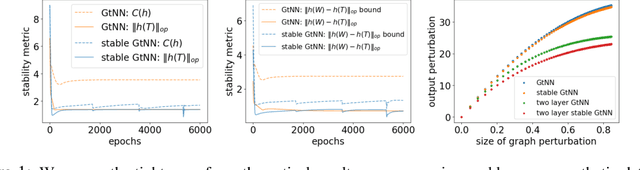
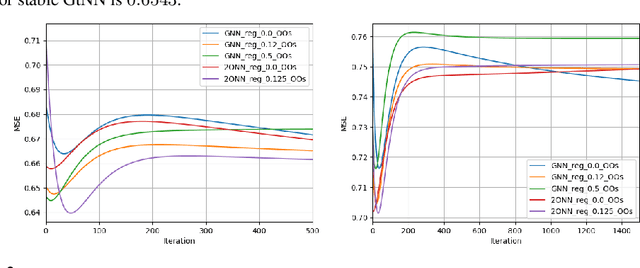
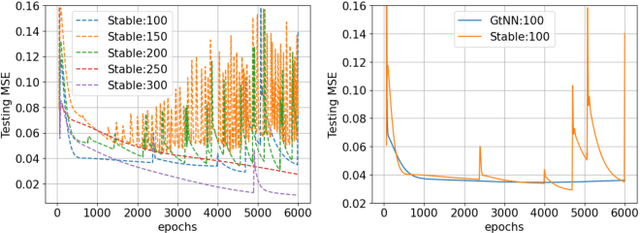
Graph neural networks (GNNs) provide state-of-the-art results in a wide variety of tasks which typically involve predicting features at the vertices of a graph. They are built from layers of graph convolutions which serve as a powerful inductive bias for describing the flow of information among the vertices. Often, more than one data modality is available. This work considers a setting in which several graphs have the same vertex set and a common vertex-level learning task. This generalizes standard GNN models to GNNs with several graph operators that do not commute. We may call this model graph-tuple neural networks (GtNN). In this work, we develop the mathematical theory to address the stability and transferability of GtNNs using properties of non-commuting non-expansive operators. We develop a limit theory of graphon-tuple neural networks and use it to prove a universal transferability theorem that guarantees that all graph-tuple neural networks are transferable on convergent graph-tuple sequences. In particular, there is no non-transferable energy under the convergence we consider here. Our theoretical results extend well-known transferability theorems for GNNs to the case of several simultaneous graphs (GtNNs) and provide a strict improvement on what is currently known even in the GNN case. We illustrate our theoretical results with simple experiments on synthetic and real-world data. To this end, we derive a training procedure that provably enforces the stability of the resulting model.

Thinner Latent Spaces: Detecting dimension and imposing invariance through autoencoder gradient constraints

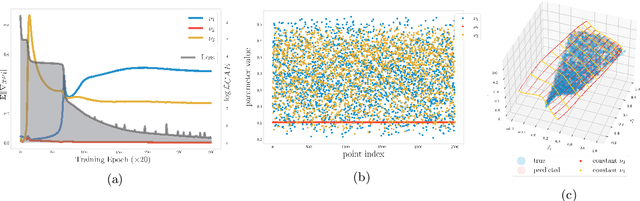
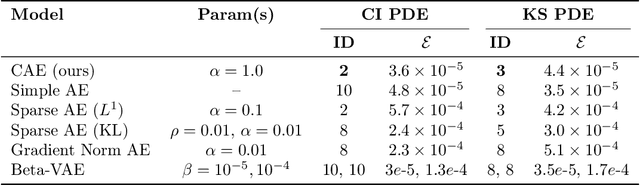
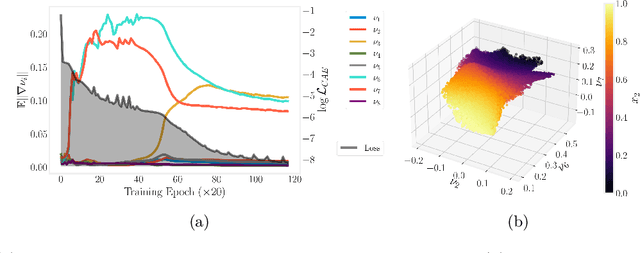
Conformal Autoencoders are a neural network architecture that imposes orthogonality conditions between the gradients of latent variables towards achieving disentangled representations of data. In this letter we show that orthogonality relations within the latent layer of the network can be leveraged to infer the intrinsic dimensionality of nonlinear manifold data sets (locally characterized by the dimension of their tangent space), while simultaneously computing encoding and decoding (embedding) maps. We outline the relevant theory relying on differential geometry, and describe the corresponding gradient-descent optimization algorithm. The method is applied to standard data sets and we highlight its applicability, advantages, and shortcomings. In addition, we demonstrate that the same computational technology can be used to build coordinate invariance to local group actions when defined only on a (reduced) submanifold of the embedding space.

Learning equivariant tensor functions with applications to sparse vector recovery

This work characterizes equivariant polynomial functions from tuples of tensor inputs to tensor outputs. Loosely motivated by physics, we focus on equivariant functions with respect to the diagonal action of the orthogonal group on tensors. We show how to extend this characterization to other linear algebraic groups, including the Lorentz and symplectic groups. Our goal behind these characterizations is to define equivariant machine learning models. In particular, we focus on the sparse vector estimation problem. This problem has been broadly studied in the theoretical computer science literature, and explicit spectral methods, derived by techniques from sum-of-squares, can be shown to recover sparse vectors under certain assumptions. Our numerical results show that the proposed equivariant machine learning models can learn spectral methods that outperform the best theoretically known spectral methods in some regimes. The experiments also suggest that learned spectral methods can solve the problem in settings that have not yet been theoretically analyzed. This is an example of a promising direction in which theory can inform machine learning models and machine learning models could inform theory.

Is machine learning good or bad for the natural sciences?

Machine learning (ML) methods are having a huge impact across all of the sciences. However, ML has a strong ontology - in which only the data exist - and a strong epistemology - in which a model is considered good if it performs well on held-out training data. These philosophies are in strong conflict with both standard practices and key philosophies in the natural sciences. Here, we identify some locations for ML in the natural sciences at which the ontology and epistemology are valuable. For example, when an expressive machine learning model is used in a causal inference to represent the effects of confounders, such as foregrounds, backgrounds, or instrument calibration parameters, the model capacity and loose philosophy of ML can make the results more trustworthy. We also show that there are contexts in which the introduction of ML introduces strong, unwanted statistical biases. For one, when ML models are used to emulate physical (or first-principles) simulations, they introduce strong confirmation biases. For another, when expressive regressions are used to label datasets, those labels cannot be used in downstream joint or ensemble analyses without taking on uncontrolled biases. The question in the title is being asked of all of the natural sciences; that is, we are calling on the scientific communities to take a step back and consider the role and value of ML in their fields; the (partial) answers we give here come from the particular perspective of physics.

Learning functions on symmetric matrices and point clouds via lightweight invariant features

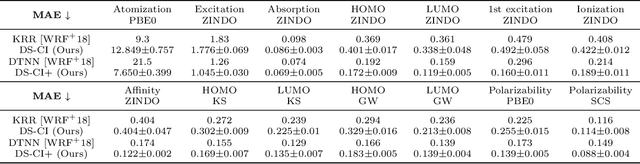
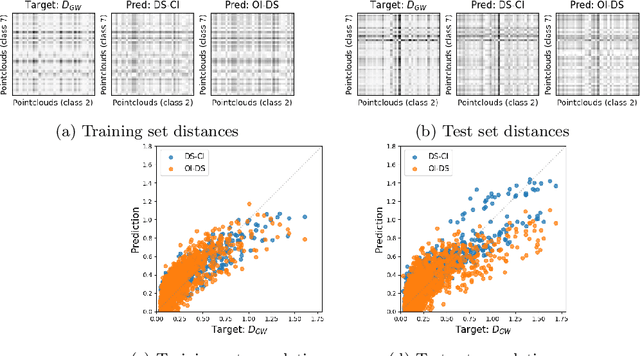
In this work, we present a mathematical formulation for machine learning of (1) functions on symmetric matrices that are invariant with respect to the action of permutations by conjugation, and (2) functions on point clouds that are invariant with respect to rotations, reflections, and permutations of the points. To achieve this, we construct $O(n^2)$ invariant features derived from generators for the field of rational functions on $n\times n$ symmetric matrices that are invariant under joint permutations of rows and columns. We show that these invariant features can separate all distinct orbits of symmetric matrices except for a measure zero set; such features can be used to universally approximate invariant functions on almost all weighted graphs. For point clouds in a fixed dimension, we prove that the number of invariant features can be reduced, generically without losing expressivity, to $O(n)$, where $n$ is the number of points. We combine these invariant features with DeepSets to learn functions on symmetric matrices and point clouds with varying sizes. We empirically demonstrate the feasibility of our approach on molecule property regression and point cloud distance prediction.

Approximately Equivariant Graph Networks

Graph neural networks (GNNs) are commonly described as being permutation equivariant with respect to node relabeling in the graph. This symmetry of GNNs is often compared to the translation equivariance symmetry of Euclidean convolution neural networks (CNNs). However, these two symmetries are fundamentally different: The translation equivariance of CNNs corresponds to symmetries of the fixed domain acting on the image signal (sometimes known as active symmetries), whereas in GNNs any permutation acts on both the graph signals and the graph domain (sometimes described as passive symmetries). In this work, we focus on the active symmetries of GNNs, by considering a learning setting where signals are supported on a fixed graph. In this case, the natural symmetries of GNNs are the automorphisms of the graph. Since real-world graphs tend to be asymmetric, we relax the notion of symmetries by formalizing approximate symmetries via graph coarsening. We present a bias-variance formula that quantifies the tradeoff between the loss in expressivity and the gain in the regularity of the learned estimator, depending on the chosen symmetry group. To illustrate our approach, we conduct extensive experiments on image inpainting, traffic flow prediction, and human pose estimation with different choices of symmetries. We show theoretically and empirically that the best generalization performance can be achieved by choosing a suitably larger group than the graph automorphism group, but smaller than the full permutation group.

Structuring Representation Geometry with Rotationally Equivariant Contrastive Learning

Self-supervised learning converts raw perceptual data such as images to a compact space where simple Euclidean distances measure meaningful variations in data. In this paper, we extend this formulation by adding additional geometric structure to the embedding space by enforcing transformations of input space to correspond to simple (i.e., linear) transformations of embedding space. Specifically, in the contrastive learning setting, we introduce an equivariance objective and theoretically prove that its minima forces augmentations on input space to correspond to rotations on the spherical embedding space. We show that merely combining our equivariant loss with a non-collapse term results in non-trivial representations, without requiring invariance to data augmentations. Optimal performance is achieved by also encouraging approximate invariance, where input augmentations correspond to small rotations. Our method, CARE: Contrastive Augmentation-induced Rotational Equivariance, leads to improved performance on downstream tasks, and ensures sensitivity in embedding space to important variations in data (e.g., color) that standard contrastive methods do not achieve. Code is available at https://github.com/Sharut/CARE.