Learning equivariant tensor functions with applications to sparse vector recovery

This work characterizes equivariant polynomial functions from tuples of tensor inputs to tensor outputs. Loosely motivated by physics, we focus on equivariant functions with respect to the diagonal action of the orthogonal group on tensors. We show how to extend this characterization to other linear algebraic groups, including the Lorentz and symplectic groups. Our goal behind these characterizations is to define equivariant machine learning models. In particular, we focus on the sparse vector estimation problem. This problem has been broadly studied in the theoretical computer science literature, and explicit spectral methods, derived by techniques from sum-of-squares, can be shown to recover sparse vectors under certain assumptions. Our numerical results show that the proposed equivariant machine learning models can learn spectral methods that outperform the best theoretically known spectral methods in some regimes. The experiments also suggest that learned spectral methods can solve the problem in settings that have not yet been theoretically analyzed. This is an example of a promising direction in which theory can inform machine learning models and machine learning models could inform theory.

Laplace-HDC: Understanding the geometry of binary hyperdimensional computing

This paper studies the geometry of binary hyperdimensional computing (HDC), a computational scheme in which data are encoded using high-dimensional binary vectors. We establish a result about the similarity structure induced by the HDC binding operator and show that the Laplace kernel naturally arises in this setting, motivating our new encoding method Laplace-HDC, which improves upon previous methods. We describe how our results indicate limitations of binary HDC in encoding spatial information from images and discuss potential solutions, including using Haar convolutional features and the definition of a translation-equivariant HDC encoding. Several numerical experiments highlighting the improved accuracy of Laplace-HDC in contrast to alternative methods are presented. We also numerically study other aspects of the proposed framework such as robustness and the underlying translation-equivariant encoding.

Moment-based metrics for molecules computable from cryo-EM images

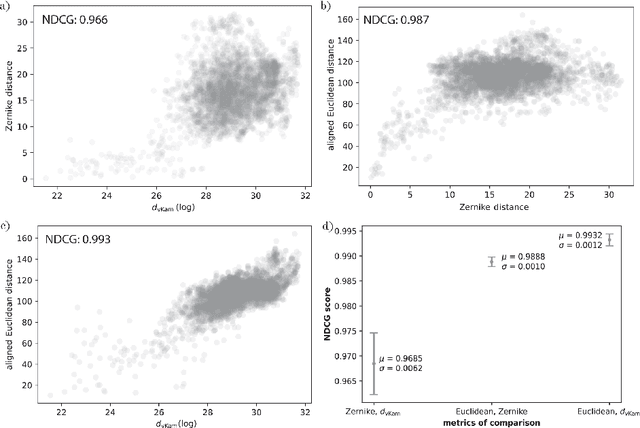
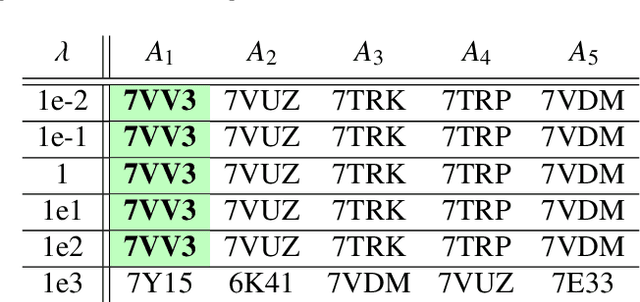
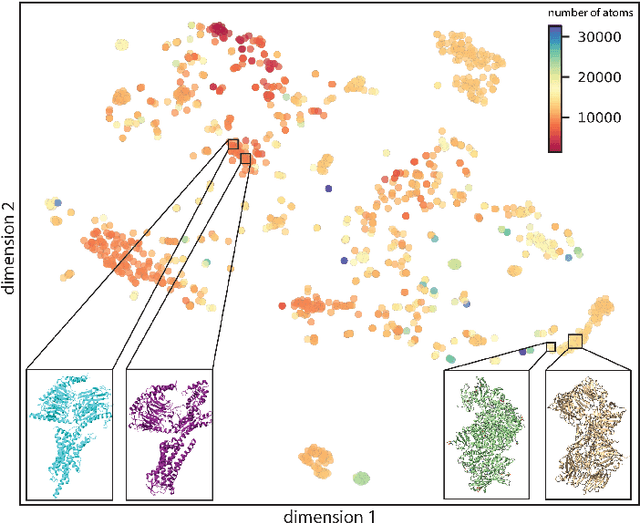
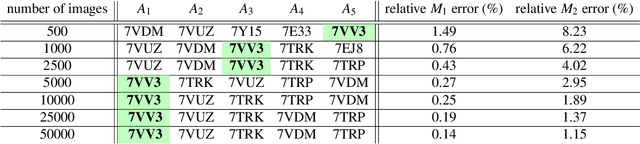
Single particle cryogenic electron microscopy (cryo-EM) is an imaging technique capable of recovering the high-resolution 3-D structure of biological macromolecules from many noisy and randomly oriented projection images. One notable approach to 3-D reconstruction, known as Kam's method, relies on the moments of the 2-D images. Inspired by Kam's method, we introduce a rotationally invariant metric between two molecular structures, which does not require 3-D alignment. Further, we introduce a metric between a stack of projection images and a molecular structure, which is invariant to rotations and reflections and does not require performing 3-D reconstruction. Additionally, the latter metric does not assume a uniform distribution of viewing angles. We demonstrate uses of the new metrics on synthetic and experimental datasets, highlighting their ability to measure structural similarity.

Randomized Kaczmarz with geometrically smoothed momentum

This paper studies the effect of adding geometrically smoothed momentum to the randomized Kaczmarz algorithm, which is an instance of stochastic gradient descent on a linear least squares loss function. We prove a result about the expected error in the direction of singular vectors of the matrix defining the least squares loss. We present several numerical examples illustrating the utility of our result and pose several questions.

Fast expansion into harmonics on the disk: a steerable basis with fast radial convolutions

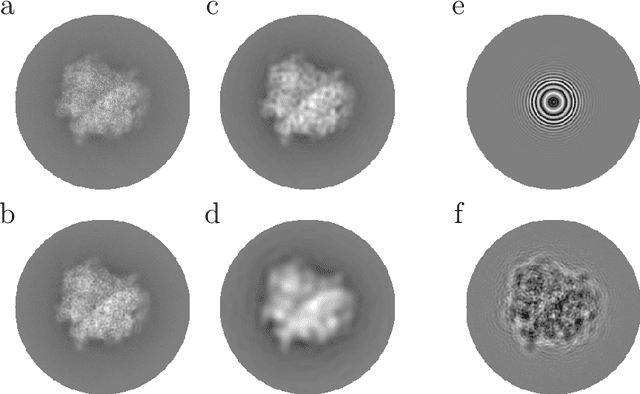
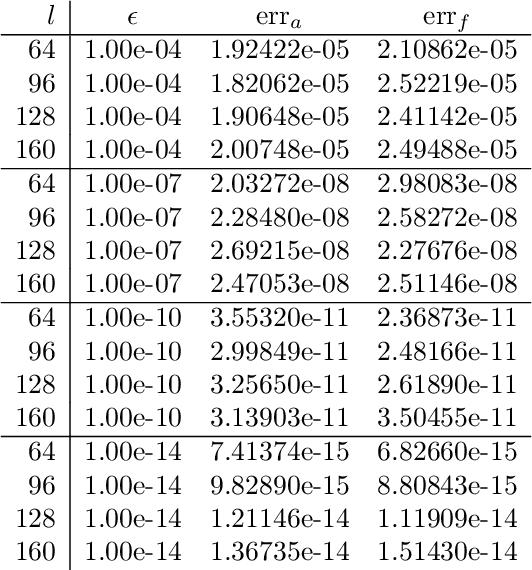
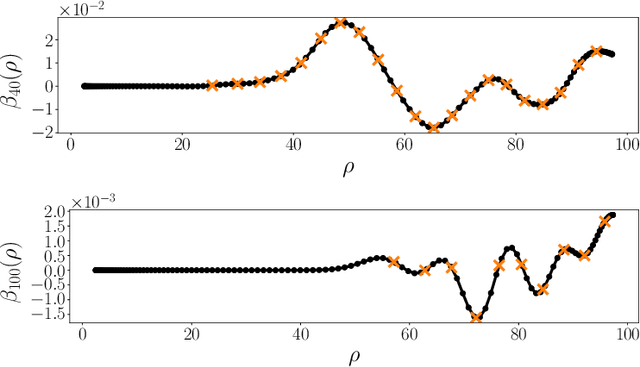
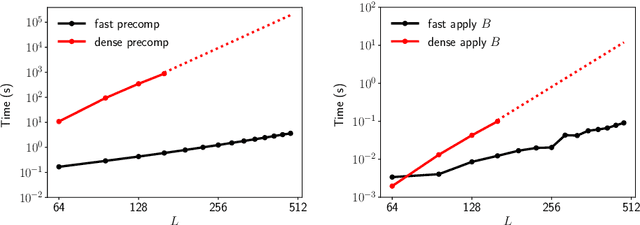
We present a fast and numerically accurate method for expanding digitized $L \times L$ images representing functions on $[-1,1]^2$ supported on the disk $\{x \in \mathbb{R}^2 : |x|<1\}$ in the harmonics (Dirichlet Laplacian eigenfunctions) on the disk. Our method runs in $\mathcal{O}(L^2 \log L)$ operations. This basis is also known as the Fourier-Bessel basis and it has several computational advantages: it is orthogonal, ordered by frequency, and steerable in the sense that images expanded in the basis can be rotated by applying a diagonal transform to the coefficients. Moreover, we show that convolution with radial functions can also be efficiently computed by applying a diagonal transform to the coefficients.

An optimal scheduled learning rate for a randomized Kaczmarz algorithm

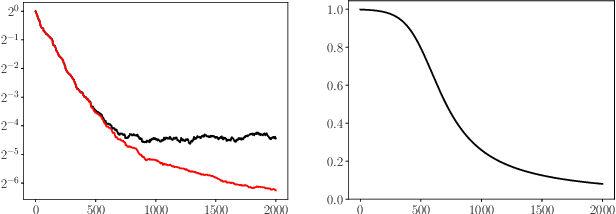
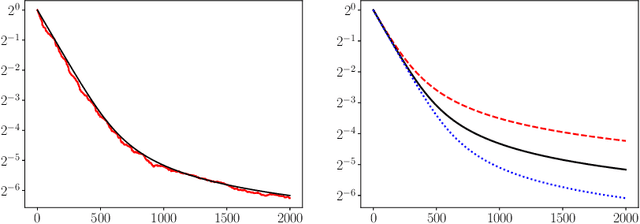
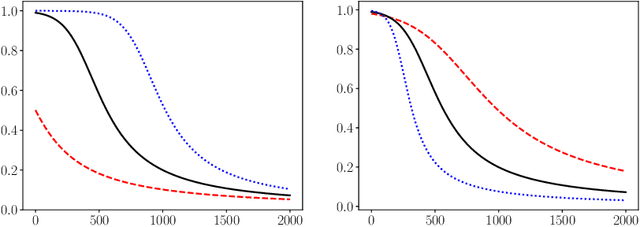
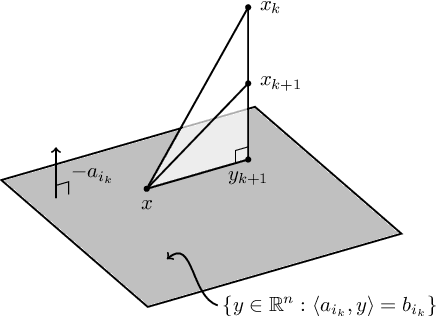
We study how the learning rate affects the performance of a relaxed randomized Kaczmarz algorithm for solving $A x \approx b + \varepsilon$, where $A x =b$ is a consistent linear system and $\varepsilon$ has independent mean zero random entries. We derive a learning rate schedule which optimizes a bound on the expected error that is sharp in certain cases; in contrast to the exponential convergence of the standard randomized Kaczmarz algorithm, our optimized bound involves the reciprocal of the Lambert-$W$ function of an exponential.

A common variable minimax theorem for graphs

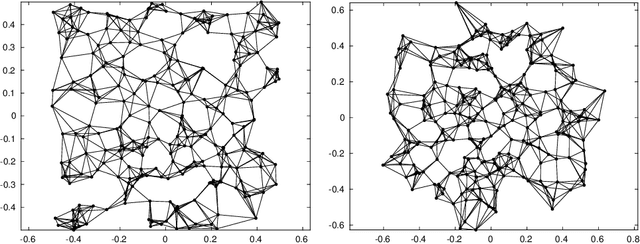
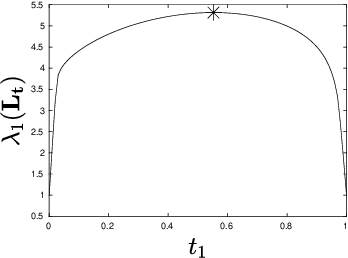
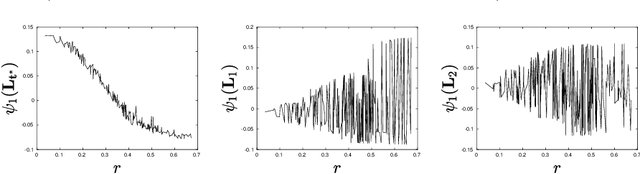
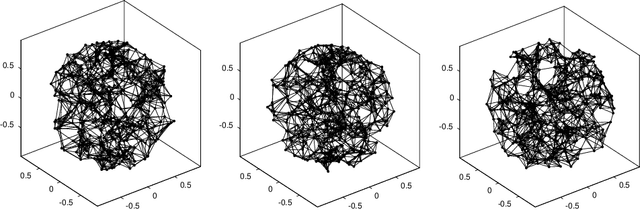
Let $\mathcal{G} = \{G_1 = (V, E_1), \dots, G_m = (V, E_m)\}$ be a collection of $m$ graphs defined on a common set of vertices $V$ but with different edge sets $E_1, \dots, E_m$. Informally, a function $f :V \rightarrow \mathbb{R}$ is smooth with respect to $G_k = (V,E_k)$ if $f(u) \sim f(v)$ whenever $(u, v) \in E_k$. We study the problem of understanding whether there exists a nonconstant function that is smooth with respect to all graphs in $\mathcal{G}$, simultaneously, and how to find it if it exists.

Multi-target detection with rotations

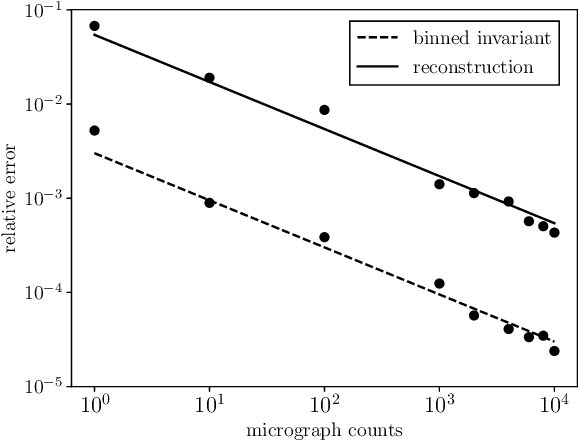
We consider the multi-target detection problem of estimating a two-dimensional target image from a large noisy measurement image that contains many randomly rotated and translated copies of the target image. Motivated by single-particle cryo-electron microscopy, we focus on the low signal-to-noise regime, where it is difficult to estimate the locations and orientations of the target images in the measurement. Our approach uses autocorrelation analysis to estimate rotationally and translationally invariant features of the target image. We demonstrate that, regardless of the level of noise, our technique can be used to recover the target image when the measurement is sufficiently large.

Image recovery from rotational and translational invariants

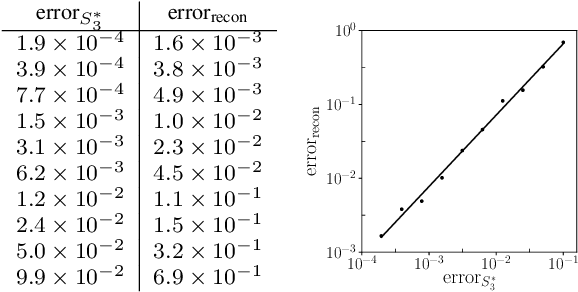
We introduce a framework for recovering an image from its rotationally and translationally invariant features based on autocorrelation analysis. This work is an instance of the multi-target detection statistical model, which is mainly used to study the mathematical and computational properties of single-particle reconstruction using cryo-electron microscopy (cryo-EM) at low signal-to-noise ratios. We demonstrate with synthetic numerical experiments that an image can be reconstructed from rotationally and translationally invariant features and show that the reconstruction is robust to noise. These results constitute an important step towards the goal of structure determination of small biomolecules using cryo-EM.

Manifold learning with bi-stochastic kernels

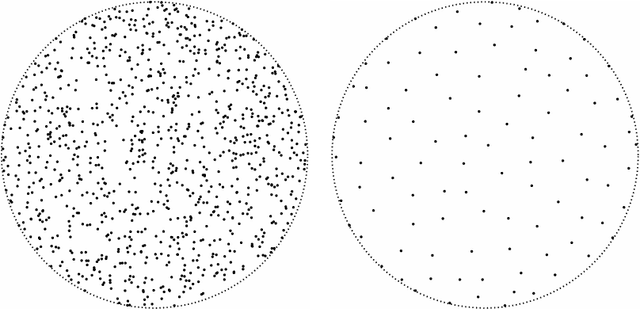
In this paper we answer the following question: what is the infinitesimal generator of the diffusion process defined by a kernel that is normalized such that it is bi-stochastic with respect to a specified measure? More precisely, under the assumption that data is sampled from a Riemannian manifold we determine how the resulting infinitesimal generator depends on the potentially nonuniform distribution of the sample points, and the specified measure for the bi-stochastic normalization. In a special case, we demonstrate a connection to the heat kernel. We consider both the case where only a single data set is given, and the case where a data set and a reference set are given. The spectral theory of the constructed operators is studied, and Nystr\"om extension formulas for the gradients of the eigenfunctions are computed. Applications to discrete point sets and manifold learning are discussed.