Randomly Pivoted Partial Cholesky: Random How?

We consider the problem of finding good low rank approximations of symmetric, positive-definite $A \in \mathbb{R}^{n \times n}$. Chen-Epperly-Tropp-Webber showed, among many other things, that the randomly pivoted partial Cholesky algorithm that chooses the $i-$th row with probability proportional to the diagonal entry $A_{ii}$ leads to a universal contraction of the trace norm (the Schatten 1-norm) in expectation for each step. We show that if one chooses the $i-$th row with likelihood proportional to $A_{ii}^2$ one obtains the same result in the Frobenius norm (the Schatten 2-norm). Implications for the greedy pivoting rule and pivot selection strategies are discussed.

May the force be with you

Modern methods in dimensionality reduction are dominated by nonlinear attraction-repulsion force-based methods (this includes t-SNE, UMAP, ForceAtlas2, LargeVis, and many more). The purpose of this paper is to demonstrate that all such methods, by design, come with an additional feature that is being automatically computed along the way, namely the vector field associated with these forces. We show how this vector field gives additional high-quality information and propose a general refinement strategy based on ideas from Morse theory. The efficiency of these ideas is illustrated specifically using t-SNE on synthetic and real-life data sets.

A common variable minimax theorem for graphs

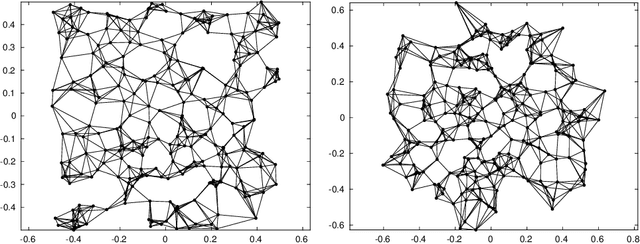
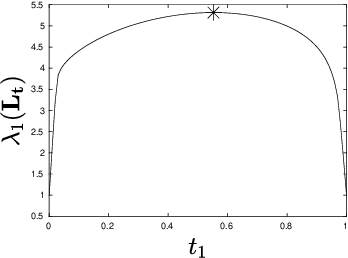
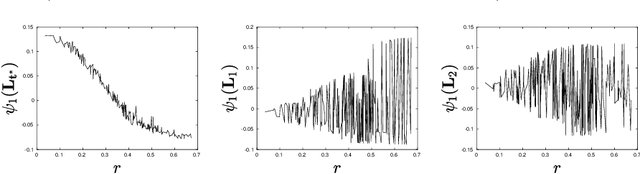
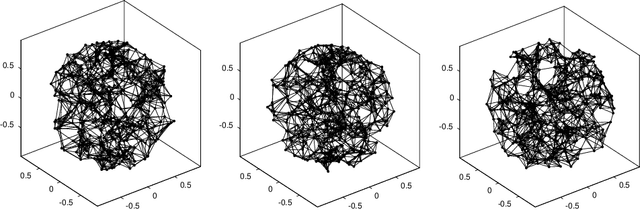
Let $\mathcal{G} = \{G_1 = (V, E_1), \dots, G_m = (V, E_m)\}$ be a collection of $m$ graphs defined on a common set of vertices $V$ but with different edge sets $E_1, \dots, E_m$. Informally, a function $f :V \rightarrow \mathbb{R}$ is smooth with respect to $G_k = (V,E_k)$ if $f(u) \sim f(v)$ whenever $(u, v) \in E_k$. We study the problem of understanding whether there exists a nonconstant function that is smooth with respect to all graphs in $\mathcal{G}$, simultaneously, and how to find it if it exists.

t-SNE, Forceful Colorings and Mean Field Limits

t-SNE is one of the most commonly used force-based nonlinear dimensionality reduction methods. This paper has two contributions: the first is forceful colorings, an idea that is also applicable to other force-based methods (UMAP, ForceAtlas2,...). In every equilibrium, the attractive and repulsive forces acting on a particle cancel out: however, both the size and the direction of the attractive (or repulsive) forces acting on a particle are related to its properties: the force vector can serve as an additional feature. Secondly, we analyze the case of t-SNE acting on a single homogeneous cluster (modeled by affinities coming from the adjacency matrix of a random k-regular graph); we derive a mean-field model that leads to interesting questions in classical calculus of variations. The model predicts that, in the limit, the t-SNE embedding of a single perfectly homogeneous cluster is not a point but a thin annulus of diameter $\sim k^{-1/4} n^{-1/4}$. This is supported by numerical results. The mean field ansatz extends to other force-based dimensionality reduction methods.

Neural Collapse with Cross-Entropy Loss

We consider the variational problem of cross-entropy loss with $n$ feature vectors on a unit hypersphere in $\mathbb{R}^d$. We prove that when $d \geq n - 1$, the global minimum is given by the simplex equiangular tight frame, which justifies the neural collapse behavior. We also prove that as $n \rightarrow \infty$ with fixed $d$, the minimizing points will distribute uniformly on the hypersphere and show a connection with the frame potential of Benedetto & Fickus.

On the Regularization Effect of Stochastic Gradient Descent applied to Least Squares

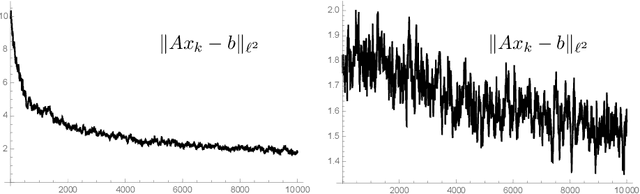
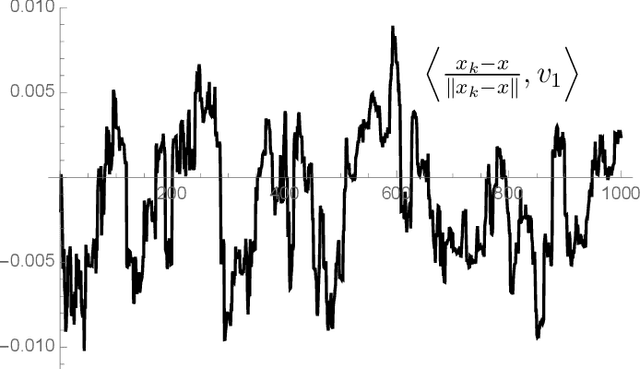
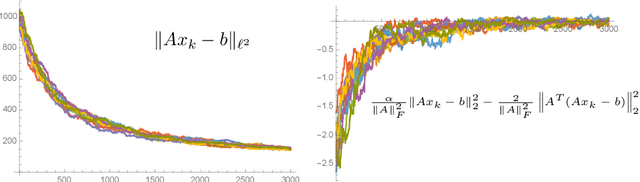
We study the behavior of stochastic gradient descent applied to $\|Ax -b \|_2^2 \rightarrow \min$ for invertible $A \in \mathbb{R}^{n \times n}$. We show that there is an explicit constant $c_{A}$ depending (mildly) on $A$ such that $$ \mathbb{E} ~\left\| Ax_{k+1}-b\right\|^2_{2} \leq \left(1 + \frac{c_{A}}{\|A\|_F^2}\right) \left\|A x_k -b \right\|^2_{2} - \frac{2}{\|A\|_F^2} \left\|A^T A (x_k - x)\right\|^2_{2}.$$ This is a curious inequality: the last term has one more matrix applied to the residual $u_k - u$ than the remaining terms: if $x_k - x$ is mainly comprised of large singular vectors, stochastic gradient descent leads to a quick regularization. For symmetric matrices, this inequality has an extension to higher-order Sobolev spaces. This explains a (known) regularization phenomenon: an energy cascade from large singular values to small singular values smoothes.

Spectral Clustering Revisited: Information Hidden in the Fiedler Vector

We are interested in the clustering problem on graphs: it is known that if there are two underlying clusters, then the signs of the eigenvector corresponding to the second largest eigenvalue of the adjacency matrix can reliably reconstruct the two clusters. We argue that the vertices for which the eigenvector has the largest and the smallest entries, respectively, are unusually strongly connected to their own cluster and more reliably classified than the rest. This can be regarded as a discrete version of the Hot Spots conjecture and should be useful in applications. We give a rigorous proof for the stochastic block model and several examples.

The Spectral Underpinning of word2vec

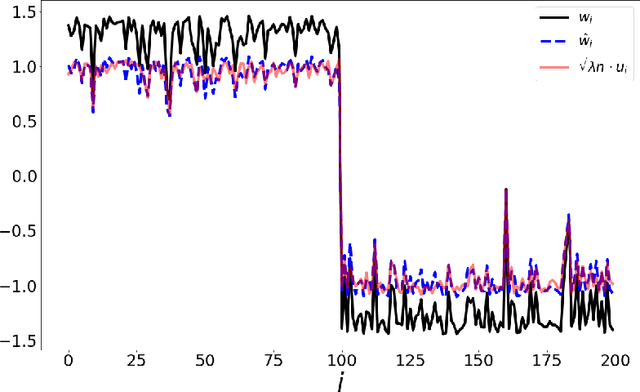
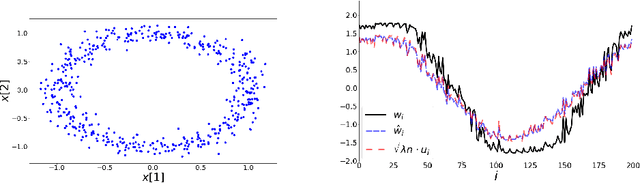
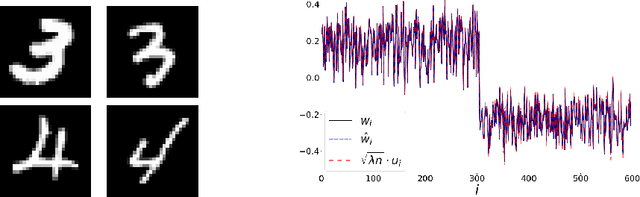
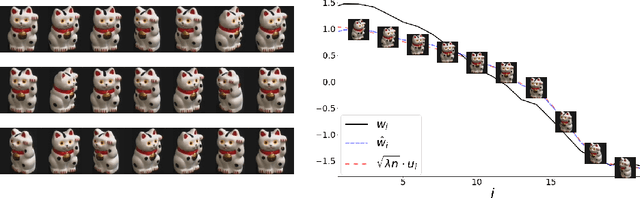
word2vec due to Mikolov \textit{et al.} (2013) is a word embedding method that is widely used in natural language processing. Despite its great success and frequent use, theoretical justification is still lacking. The main contribution of our paper is to propose a rigorous analysis of the highly nonlinear functional of word2vec. Our results suggest that word2vec may be primarily driven by an underlying spectral method. This insight may open the door to obtaining provable guarantees for word2vec. We support these findings by numerical simulations. One fascinating open question is whether the nonlinear properties of word2vec that are not captured by the spectral method are beneficial and, if so, by what mechanism.

Heavy-tailed kernels reveal a finer cluster structure in t-SNE visualisations

T-distributed stochastic neighbour embedding (t-SNE) is a widely used data visualisation technique. It differs from its predecessor SNE by the low-dimensional similarity kernel: the Gaussian kernel was replaced by the heavy-tailed Cauchy kernel, solving the "crowding problem" of SNE. Here, we develop an efficient implementation of t-SNE for a $t$-distribution kernel with an arbitrary degree of freedom $\nu$, with $\nu\to\infty$ corresponding to SNE and $\nu=1$ corresponding to the standard t-SNE. Using theoretical analysis and toy examples, we show that $\nu<1$ can further reduce the crowding problem and reveal finer cluster structure that is invisible in standard t-SNE. We further demonstrate the striking effect of heavier-tailed kernels on large real-life data sets such as MNIST, single-cell RNA-sequencing data, and the HathiTrust library. We use domain knowledge to confirm that the revealed clusters are meaningful. Overall, we argue that modifying the tail heaviness of the t-SNE kernel can yield additional insight into the cluster structure of the data.

Recovering Trees with Convex Clustering

Convex clustering refers, for given $\left\{x_1, \dots, x_n\right\} \subset \mathbb{R}^p$, to the minimization of \begin{eqnarray*} u(\gamma) & = & \underset{u_1, \dots, u_n }{\arg\min}\;\sum_{i=1}^{n}{\lVert x_i - u_i \rVert^2} + \gamma \sum_{i,j=1}^{n}{w_{ij} \lVert u_i - u_j\rVert},\\ \end{eqnarray*} where $w_{ij} \geq 0$ is an affinity that quantifies the similarity between $x_i$ and $x_j$. We prove that if the affinities $w_{ij}$ reflect a tree structure in the $\left\{x_1, \dots, x_n\right\}$, then the convex clustering solution path reconstructs the tree exactly. The main technical ingredient implies the following combinatorial byproduct: for every set $\left\{x_1, \dots, x_n \right\} \subset \mathbb{R}^p$ of $n \geq 2$ distinct points, there exist at least $n/6$ points with the property that for any of these points $x$ there is a unit vector $v \in \mathbb{R}^p$ such that, when viewed from $x$, `most' points lie in the direction $v$ \begin{eqnarray*} \frac{1}{n-1}\sum_{i=1 \atop x_i \neq x}^{n}{ \left\langle \frac{x_i - x}{\lVert x_i - x \rVert}, v \right\rangle} & \geq & \frac{1}{4}. \end{eqnarray*}