Dmitry Kobak
University of Tübingen
Node Embeddings via Neighbor Embeddings
Mar 31, 2025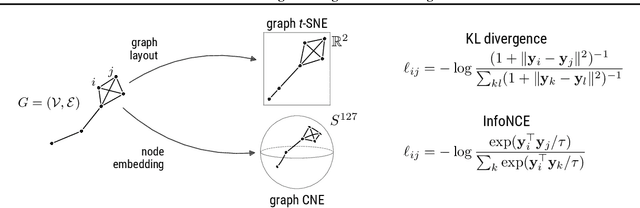
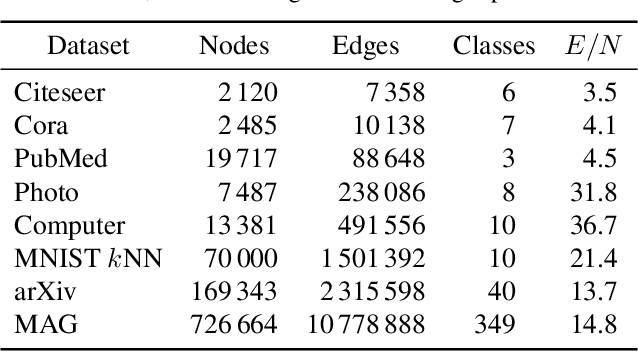
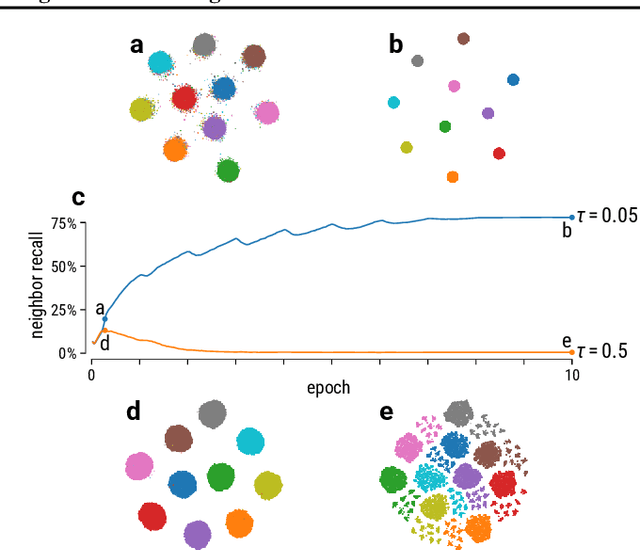
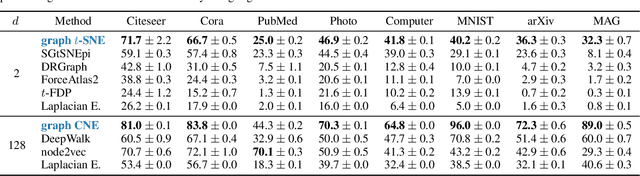
Abstract:Graph layouts and node embeddings are two distinct paradigms for non-parametric graph representation learning. In the former, nodes are embedded into 2D space for visualization purposes. In the latter, nodes are embedded into a high-dimensional vector space for downstream processing. State-of-the-art algorithms for these two paradigms, force-directed layouts and random-walk-based contrastive learning (such as DeepWalk and node2vec), have little in common. In this work, we show that both paradigms can be approached with a single coherent framework based on established neighbor embedding methods. Specifically, we introduce graph t-SNE, a neighbor embedding method for two-dimensional graph layouts, and graph CNE, a contrastive neighbor embedding method that produces high-dimensional node representations by optimizing the InfoNCE objective. We show that both graph t-SNE and graph CNE strongly outperform state-of-the-art algorithms in terms of local structure preservation, while being conceptually simpler.
On the Importance of Embedding Norms in Self-Supervised Learning
Feb 13, 2025Abstract:Self-supervised learning (SSL) allows training data representations without a supervised signal and has become an important paradigm in machine learning. Most SSL methods employ the cosine similarity between embedding vectors and hence effectively embed data on a hypersphere. While this seemingly implies that embedding norms cannot play any role in SSL, a few recent works have suggested that embedding norms have properties related to network convergence and confidence. In this paper, we resolve this apparent contradiction and systematically establish the embedding norm's role in SSL training. Using theoretical analysis, simulations, and experiments, we show that embedding norms (i) govern SSL convergence rates and (ii) encode network confidence, with smaller norms corresponding to unexpected samples. Additionally, we show that manipulating embedding norms can have large effects on convergence speed. Our findings demonstrate that SSL embedding norms are integral to understanding and optimizing network behavior.
Delving into ChatGPT usage in academic writing through excess vocabulary
Jun 11, 2024Abstract:Recent large language models (LLMs) can generate and revise text with human-level performance, and have been widely commercialized in systems like ChatGPT. These models come with clear limitations: they can produce inaccurate information, reinforce existing biases, and be easily misused. Yet, many scientists have been using them to assist their scholarly writing. How wide-spread is LLM usage in the academic literature currently? To answer this question, we use an unbiased, large-scale approach, free from any assumptions on academic LLM usage. We study vocabulary changes in 14 million PubMed abstracts from 2010-2024, and show how the appearance of LLMs led to an abrupt increase in the frequency of certain style words. Our analysis based on excess words usage suggests that at least 10% of 2024 abstracts were processed with LLMs. This lower bound differed across disciplines, countries, and journals, and was as high as 30% for some PubMed sub-corpora. We show that the appearance of LLM-based writing assistants has had an unprecedented impact in the scientific literature, surpassing the effect of major world events such as the Covid pandemic.
Learning representations of learning representations
Apr 12, 2024Abstract:The ICLR conference is unique among the top machine learning conferences in that all submitted papers are openly available. Here we present the ICLR dataset consisting of abstracts of all 24 thousand ICLR submissions from 2017-2024 with meta-data, decision scores, and custom keyword-based labels. We find that on this dataset, bag-of-words representation outperforms most dedicated sentence transformer models in terms of $k$NN classification accuracy, and the top performing language models barely outperform TF-IDF. We see this as a challenge for the NLP community. Furthermore, we use the ICLR dataset to study how the field of machine learning has changed over the last seven years, finding some improvement in gender balance. Using a 2D embedding of the abstracts' texts, we describe a shift in research topics from 2017 to 2024 and identify hedgehogs and foxes among the authors with the highest number of ICLR submissions.
Self-supervised Visualisation of Medical Image Datasets
Feb 22, 2024



Abstract:Self-supervised learning methods based on data augmentations, such as SimCLR, BYOL, or DINO, allow obtaining semantically meaningful representations of image datasets and are widely used prior to supervised fine-tuning. A recent self-supervised learning method, $t$-SimCNE, uses contrastive learning to directly train a 2D representation suitable for visualisation. When applied to natural image datasets, $t$-SimCNE yields 2D visualisations with semantically meaningful clusters. In this work, we used $t$-SimCNE to visualise medical image datasets, including examples from dermatology, histology, and blood microscopy. We found that increasing the set of data augmentations to include arbitrary rotations improved the results in terms of class separability, compared to data augmentations used for natural images. Our 2D representations show medically relevant structures and can be used to aid data exploration and annotation, improving on common approaches for data visualisation.
Persistent homology for high-dimensional data based on spectral methods
Nov 06, 2023



Abstract:Persistent homology is a popular computational tool for detecting non-trivial topology of point clouds, such as the presence of loops or voids. However, many real-world datasets with low intrinsic dimensionality reside in an ambient space of much higher dimensionality. We show that in this case vanilla persistent homology becomes very sensitive to noise and fails to detect the correct topology. The same holds true for most existing refinements of persistent homology. As a remedy, we find that spectral distances on the $k$-nearest-neighbor graph of the data, such as diffusion distance and effective resistance, allow persistent homology to detect the correct topology even in the presence of high-dimensional noise. Furthermore, we derive a novel closed-form expression for effective resistance in terms of the eigendecomposition of the graph Laplacian, and describe its relation to diffusion distances. Finally, we apply these methods to several high-dimensional single-cell RNA-sequencing datasets and show that spectral distances on the $k$-nearest-neighbor graph allow robust detection of cell cycle loops.
Unsupervised visualization of image datasets using contrastive learning
Oct 18, 2022



Abstract:Visualization methods based on the nearest neighbor graph, such as t-SNE or UMAP, are widely used for visualizing high-dimensional data. Yet, these approaches only produce meaningful results if the nearest neighbors themselves are meaningful. For images represented in pixel space this is not the case, as distances in pixel space are often not capturing our sense of similarity and therefore neighbors are not semantically close. This problem can be circumvented by self-supervised approaches based on contrastive learning, such as SimCLR, relying on data augmentation to generate implicit neighbors, but these methods do not produce two-dimensional embeddings suitable for visualization. Here, we present a new method, called t-SimCNE, for unsupervised visualization of image data. T-SimCNE combines ideas from contrastive learning and neighbor embeddings, and trains a parametric mapping from the high-dimensional pixel space into two dimensions. We show that the resulting 2D embeddings achieve classification accuracy comparable to the state-of-the-art high-dimensional SimCLR representations, thus faithfully capturing semantic relationships. Using t-SimCNE, we obtain informative visualizations of the CIFAR-10 and CIFAR-100 datasets, showing rich cluster structure and highlighting artifacts and outliers.
Contrastive learning unifies $t$-SNE and UMAP
Jun 03, 2022



Abstract:Neighbor embedding methods $t$-SNE and UMAP are the de facto standard for visualizing high-dimensional datasets. They appear to use very different loss functions with different motivations, and the exact relationship between them has been unclear. Here we show that UMAP is effectively negative sampling applied to the $t$-SNE loss function. We explain the difference between negative sampling and noise-contrastive estimation (NCE), which has been used to optimize $t$-SNE under the name NCVis. We prove that, unlike NCE, negative sampling learns a scaled data distribution. When applied in the neighbor embedding setting, it yields more compact embeddings with increased attraction, explaining differences in appearance between UMAP and $t$-SNE. Further, we generalize the notion of negative sampling and obtain a spectrum of embeddings, encompassing visualizations similar to $t$-SNE, NCVis, and UMAP. Finally, we explore the connection between representation learning in the SimCLR setting and neighbor embeddings, and show that (i) $t$-SNE can be optimized using the InfoNCE loss and in a parametric setting; (ii) various contrastive losses with only few noise samples can yield competitive performance in the SimCLR setup.
Wasserstein t-SNE
May 16, 2022



Abstract:Scientific datasets often have hierarchical structure: for example, in surveys, individual participants (samples) might be grouped at a higher level (units) such as their geographical region. In these settings, the interest is often in exploring the structure on the unit level rather than on the sample level. Units can be compared based on the distance between their means, however this ignores the within-unit distribution of samples. Here we develop an approach for exploratory analysis of hierarchical datasets using the Wasserstein distance metric that takes into account the shapes of within-unit distributions. We use t-SNE to construct 2D embeddings of the units, based on the matrix of pairwise Wasserstein distances between them. The distance matrix can be efficiently computed by approximating each unit with a Gaussian distribution, but we also provide a scalable method to compute exact Wasserstein distances. We use synthetic data to demonstrate the effectiveness of our Wasserstein t-SNE, and apply it to data from the 2017 German parliamentary election, considering polling stations as samples and voting districts as units. The resulting embedding uncovers meaningful structure in the data.
A Unifying Perspective on Neighbor Embeddings along the Attraction-Repulsion Spectrum
Jul 17, 2020



Abstract:Neighbor embeddings are a family of methods for visualizing complex high-dimensional datasets using kNN graphs. To find the low-dimensional embedding, these algorithms combine an attractive force between neighboring pairs of points with a repulsive force between all points. One of the most popular examples of such algorithms is t-SNE. Here we show that changing the balance between the attractive and the repulsive forces in t-SNE yields a spectrum of embeddings, which is characterized by a simple trade-off: stronger attraction can better represent continuous manifold structures, while stronger repulsion can better represent discrete cluster structures. We show that UMAP embeddings correspond to t-SNE with increased attraction; this happens because the negative sampling optimisation strategy employed by UMAP strongly lowers the effective repulsion. Likewise, ForceAtlas2, commonly used for visualizing developmental single-cell transcriptomic data, yields embeddings corresponding to t-SNE with the attraction increased even more. At the extreme of this spectrum lies Laplacian Eigenmaps, corresponding to zero repulsion. Our results demonstrate that many prominent neighbor embedding algorithms can be placed onto this attraction-repulsion spectrum, and highlight the inherent trade-offs between them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge