Jan Niklas Böhm
University of Tübingen
Node Embeddings via Neighbor Embeddings
Mar 31, 2025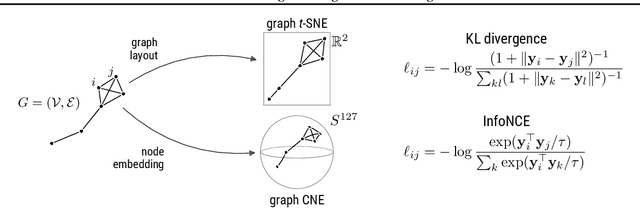
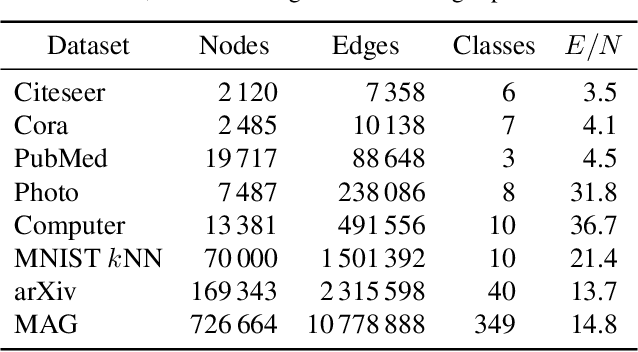
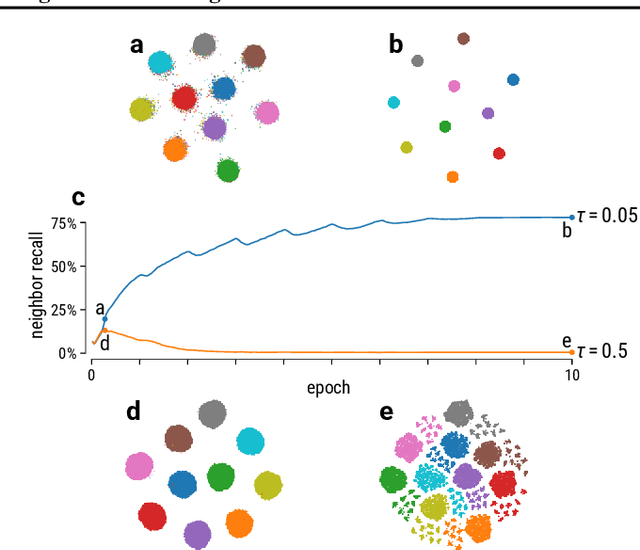
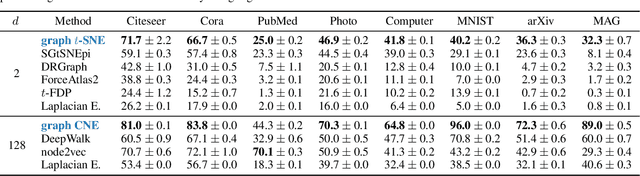
Abstract:Graph layouts and node embeddings are two distinct paradigms for non-parametric graph representation learning. In the former, nodes are embedded into 2D space for visualization purposes. In the latter, nodes are embedded into a high-dimensional vector space for downstream processing. State-of-the-art algorithms for these two paradigms, force-directed layouts and random-walk-based contrastive learning (such as DeepWalk and node2vec), have little in common. In this work, we show that both paradigms can be approached with a single coherent framework based on established neighbor embedding methods. Specifically, we introduce graph t-SNE, a neighbor embedding method for two-dimensional graph layouts, and graph CNE, a contrastive neighbor embedding method that produces high-dimensional node representations by optimizing the InfoNCE objective. We show that both graph t-SNE and graph CNE strongly outperform state-of-the-art algorithms in terms of local structure preservation, while being conceptually simpler.
On the Importance of Embedding Norms in Self-Supervised Learning
Feb 13, 2025Abstract:Self-supervised learning (SSL) allows training data representations without a supervised signal and has become an important paradigm in machine learning. Most SSL methods employ the cosine similarity between embedding vectors and hence effectively embed data on a hypersphere. While this seemingly implies that embedding norms cannot play any role in SSL, a few recent works have suggested that embedding norms have properties related to network convergence and confidence. In this paper, we resolve this apparent contradiction and systematically establish the embedding norm's role in SSL training. Using theoretical analysis, simulations, and experiments, we show that embedding norms (i) govern SSL convergence rates and (ii) encode network confidence, with smaller norms corresponding to unexpected samples. Additionally, we show that manipulating embedding norms can have large effects on convergence speed. Our findings demonstrate that SSL embedding norms are integral to understanding and optimizing network behavior.
Self-supervised Visualisation of Medical Image Datasets
Feb 22, 2024



Abstract:Self-supervised learning methods based on data augmentations, such as SimCLR, BYOL, or DINO, allow obtaining semantically meaningful representations of image datasets and are widely used prior to supervised fine-tuning. A recent self-supervised learning method, $t$-SimCNE, uses contrastive learning to directly train a 2D representation suitable for visualisation. When applied to natural image datasets, $t$-SimCNE yields 2D visualisations with semantically meaningful clusters. In this work, we used $t$-SimCNE to visualise medical image datasets, including examples from dermatology, histology, and blood microscopy. We found that increasing the set of data augmentations to include arbitrary rotations improved the results in terms of class separability, compared to data augmentations used for natural images. Our 2D representations show medically relevant structures and can be used to aid data exploration and annotation, improving on common approaches for data visualisation.
Unsupervised visualization of image datasets using contrastive learning
Oct 18, 2022



Abstract:Visualization methods based on the nearest neighbor graph, such as t-SNE or UMAP, are widely used for visualizing high-dimensional data. Yet, these approaches only produce meaningful results if the nearest neighbors themselves are meaningful. For images represented in pixel space this is not the case, as distances in pixel space are often not capturing our sense of similarity and therefore neighbors are not semantically close. This problem can be circumvented by self-supervised approaches based on contrastive learning, such as SimCLR, relying on data augmentation to generate implicit neighbors, but these methods do not produce two-dimensional embeddings suitable for visualization. Here, we present a new method, called t-SimCNE, for unsupervised visualization of image data. T-SimCNE combines ideas from contrastive learning and neighbor embeddings, and trains a parametric mapping from the high-dimensional pixel space into two dimensions. We show that the resulting 2D embeddings achieve classification accuracy comparable to the state-of-the-art high-dimensional SimCLR representations, thus faithfully capturing semantic relationships. Using t-SimCNE, we obtain informative visualizations of the CIFAR-10 and CIFAR-100 datasets, showing rich cluster structure and highlighting artifacts and outliers.
Contrastive learning unifies $t$-SNE and UMAP
Jun 03, 2022



Abstract:Neighbor embedding methods $t$-SNE and UMAP are the de facto standard for visualizing high-dimensional datasets. They appear to use very different loss functions with different motivations, and the exact relationship between them has been unclear. Here we show that UMAP is effectively negative sampling applied to the $t$-SNE loss function. We explain the difference between negative sampling and noise-contrastive estimation (NCE), which has been used to optimize $t$-SNE under the name NCVis. We prove that, unlike NCE, negative sampling learns a scaled data distribution. When applied in the neighbor embedding setting, it yields more compact embeddings with increased attraction, explaining differences in appearance between UMAP and $t$-SNE. Further, we generalize the notion of negative sampling and obtain a spectrum of embeddings, encompassing visualizations similar to $t$-SNE, NCVis, and UMAP. Finally, we explore the connection between representation learning in the SimCLR setting and neighbor embeddings, and show that (i) $t$-SNE can be optimized using the InfoNCE loss and in a parametric setting; (ii) various contrastive losses with only few noise samples can yield competitive performance in the SimCLR setup.
A Unifying Perspective on Neighbor Embeddings along the Attraction-Repulsion Spectrum
Jul 17, 2020



Abstract:Neighbor embeddings are a family of methods for visualizing complex high-dimensional datasets using kNN graphs. To find the low-dimensional embedding, these algorithms combine an attractive force between neighboring pairs of points with a repulsive force between all points. One of the most popular examples of such algorithms is t-SNE. Here we show that changing the balance between the attractive and the repulsive forces in t-SNE yields a spectrum of embeddings, which is characterized by a simple trade-off: stronger attraction can better represent continuous manifold structures, while stronger repulsion can better represent discrete cluster structures. We show that UMAP embeddings correspond to t-SNE with increased attraction; this happens because the negative sampling optimisation strategy employed by UMAP strongly lowers the effective repulsion. Likewise, ForceAtlas2, commonly used for visualizing developmental single-cell transcriptomic data, yields embeddings corresponding to t-SNE with the attraction increased even more. At the extreme of this spectrum lies Laplacian Eigenmaps, corresponding to zero repulsion. Our results demonstrate that many prominent neighbor embedding algorithms can be placed onto this attraction-repulsion spectrum, and highlight the inherent trade-offs between them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge