Pullback Flow Matching on Data Manifolds

We propose Pullback Flow Matching (PFM), a novel framework for generative modeling on data manifolds. Unlike existing methods that assume or learn restrictive closed-form manifold mappings for training Riemannian Flow Matching (RFM) models, PFM leverages pullback geometry and isometric learning to preserve the underlying manifold's geometry while enabling efficient generation and precise interpolation in latent space. This approach not only facilitates closed-form mappings on the data manifold but also allows for designable latent spaces, using assumed metrics on both data and latent manifolds. By enhancing isometric learning through Neural ODEs and proposing a scalable training objective, we achieve a latent space more suitable for interpolation, leading to improved manifold learning and generative performance. We demonstrate PFM's effectiveness through applications in synthetic data, protein dynamics and protein sequence data, generating novel proteins with specific properties. This method shows strong potential for drug discovery and materials science, where generating novel samples with specific properties is of great interest.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

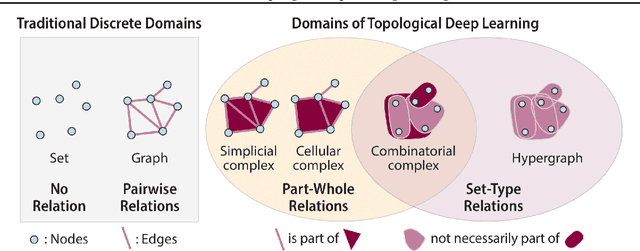
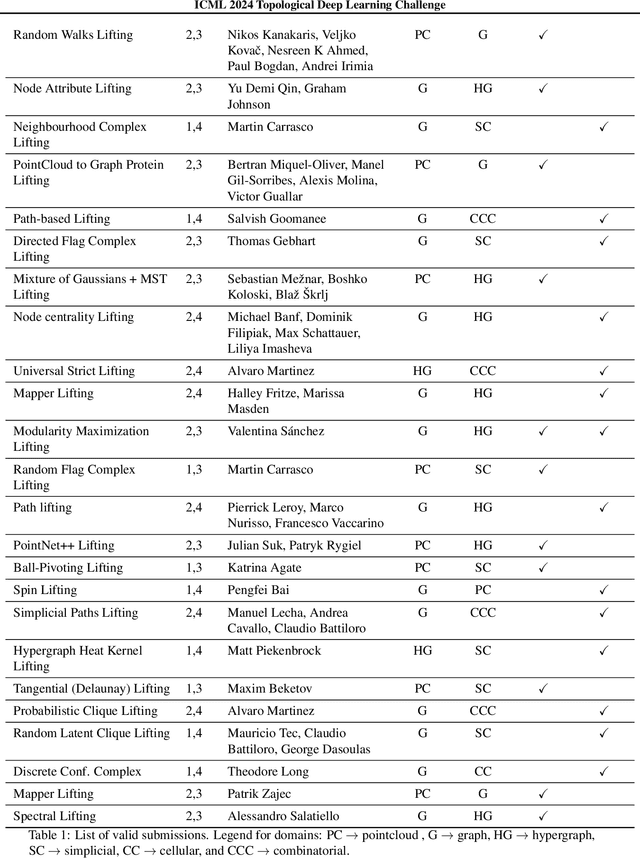
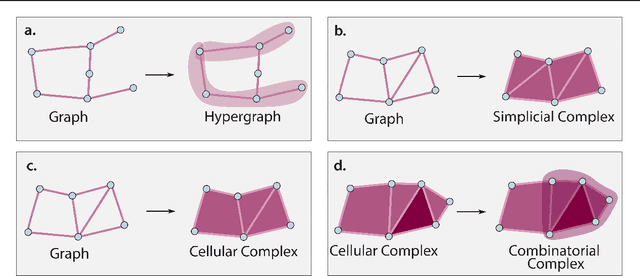
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Can strong structural encoding reduce the importance of Message Passing?

The most prevalent class of neural networks operating on graphs are message passing neural networks (MPNNs), in which the representation of a node is updated iteratively by aggregating information in the 1-hop neighborhood. Since this paradigm for computing node embeddings may prevent the model from learning coarse topological structures, the initial features are often augmented with structural information of the graph, typically in the form of Laplacian eigenvectors or Random Walk transition probabilities. In this work, we explore the contribution of message passing when strong structural encodings are provided. We introduce a novel way of modeling the interaction between feature and structural information based on their tensor product rather than the standard concatenation. The choice of interaction is compared in common scenarios and in settings where the capacity of the message-passing layer is severely reduced and ultimately the message-passing phase is removed altogether. Our results indicate that using tensor-based encodings is always at least on par with the concatenation-based encoding and that it makes the model much more robust when the message passing layers are removed, on some tasks incurring almost no drop in performance. This suggests that the importance of message passing is limited when the model can construct strong structural encodings.

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

$\mathrm{E}(n)$ Equivariant Message Passing Simplicial Networks

This paper presents $\mathrm{E}(n)$ Equivariant Message Passing Simplicial Networks (EMPSNs), a novel approach to learning on geometric graphs and point clouds that is equivariant to rotations, translations, and reflections. EMPSNs can learn high-dimensional simplex features in graphs (e.g. triangles), and use the increase of geometric information of higher-dimensional simplices in an $\mathrm{E}(n)$ equivariant fashion. EMPSNs simultaneously generalize $\mathrm{E}(n)$ Equivariant Graph Neural Networks to a topologically more elaborate counterpart and provide an approach for including geometric information in Message Passing Simplicial Networks. The results indicate that EMPSNs can leverage the benefits of both approaches, leading to a general increase in performance when compared to either method. Furthermore, the results suggest that incorporating geometric information serves as an effective measure against over-smoothing in message passing networks, especially when operating on high-dimensional simplicial structures. Last, we show that EMPSNs are on par with state-of-the-art approaches for learning on geometric graphs.

Interpretable ECG classification via a query-based latent space traversal (qLST)

Electrocardiography (ECG) is an effective and non-invasive diagnostic tool that measures the electrical activity of the heart. Interpretation of ECG signals to detect various abnormalities is a challenging task that requires expertise. Recently, the use of deep neural networks for ECG classification to aid medical practitioners has become popular, but their black box nature hampers clinical implementation. Several saliency-based interpretability techniques have been proposed, but they only indicate the location of important features and not the actual features. We present a novel interpretability technique called qLST, a query-based latent space traversal technique that is able to provide explanations for any ECG classification model. With qLST, we train a neural network that learns to traverse in the latent space of a variational autoencoder trained on a large university hospital dataset with over 800,000 ECGs annotated for 28 diseases. We demonstrate through experiments that we can explain different black box classifiers by generating ECGs through these traversals.

Geometric and Physical Quantities improve E(3) Equivariant Message Passing

Including covariant information, such as position, force, velocity or spin is important in many tasks in computational physics and chemistry. We introduce Steerable E(3) Equivariant Graph Neural Networks (SEGNNs) that generalise equivariant graph networks, such that node and edge attributes are not restricted to invariant scalars, but can contain covariant information, such as vectors or tensors. This model, composed of steerable MLPs, is able to incorporate geometric and physical information in both the message and update functions. Through the definition of steerable node attributes, the MLPs provide a new class of activation functions for general use with steerable feature fields. We discuss ours and related work through the lens of equivariant non-linear convolutions, which further allows us to pin-point the successful components of SEGNNs: non-linear message aggregation improves upon classic linear (steerable) point convolutions; steerable messages improve upon recent equivariant graph networks that send invariant messages. We demonstrate the effectiveness of our method on several tasks in computational physics and chemistry and provide extensive ablation studies.

PDE-based Group Equivariant Convolutional Neural Networks

We present a PDE-based framework that generalizes Group equivariant Convolutional Neural Networks (G-CNNs). In this framework, a network layer is seen as a set of PDE-solvers where the equation's geometrically meaningful coefficients become the layer's trainable weights. Formulating our PDEs on homogeneous spaces allows these networks to be designed with built-in symmetries such as rotation equivariance instead of being restricted to just translation equivariance as in traditional CNNs. Having all the desired symmetries included in the design obviates the need to include them by means of costly techniques such as data augmentation. Roto-translation equivariance for image analysis applications is the example we will be using throughout the paper. Our default PDE is solved by a combination of linear group convolutions and non-linear morphological group convolutions. Just like for linear convolution a morphological convolution is specified by a kernel and this kernel is what is being optimized during the training process. We demonstrate how the common CNN operations of max/min-pooling and ReLUs arise naturally from solving a PDE and how they are subsumed by morphological convolutions. We present a proof-of-concept experiment to demonstrate the potential of this framework in increasing the performance of deep learning based imaging applications.

Vesselness via Multiple Scale Orientation Scores

The multi-scale Frangi vesselness filter is an established tool in (retinal) vascular imaging. However, it cannot cope with crossings or bifurcations, since it only looks for elongated structures. Therefore, we disentangle crossing structures in the image via (multiple scale) invertible orientation scores. The described vesselness filter via scale-orientation scores performs considerably better at enhancing vessels throughout crossings and bifurcations than the Frangi version. Both methods are evaluated on a public dataset. Performance is measured by comparing ground truth data to the segmentation results obtained by basic thresholding and morphological component analysis of the filtered images.

A Multi-Orientation Analysis Approach to Retinal Vessel Tracking

This paper presents a method for retinal vasculature extraction based on biologically inspired multi-orientation analysis. We apply multi-orientation analysis via so-called invertible orientation scores, modeling the cortical columns in the visual system of higher mammals. This allows us to generically deal with many hitherto complex problems inherent to vessel tracking, such as crossings, bifurcations, parallel vessels, vessels of varying widths and vessels with high curvature. Our approach applies tracking in invertible orientation scores via a novel geometrical principle for curve optimization in the Euclidean motion group SE(2). The method runs fully automatically and provides a detailed model of the retinal vasculature, which is crucial as a sound basis for further quantitative analysis of the retina, especially in screening applications.