Cong Fu
Rethinking Generative Recommender Tokenizer: Recsys-Native Encoding and Semantic Quantization Beyond LLMs
Feb 02, 2026Abstract:Semantic ID (SID)-based recommendation is a promising paradigm for scaling sequential recommender systems, but existing methods largely follow a semantic-centric pipeline: item embeddings are learned from foundation models and discretized using generic quantization schemes. This design is misaligned with generative recommendation objectives: semantic embeddings are weakly coupled with collaborative prediction, and generic quantization is inefficient at reducing sequential uncertainty for autoregressive modeling. To address these, we propose ReSID, a recommendation-native, principled SID framework that rethinks representation learning and quantization from the perspective of information preservation and sequential predictability, without relying on LLMs. ReSID consists of two components: (i) Field-Aware Masked Auto-Encoding (FAMAE), which learns predictive-sufficient item representations from structured features, and (ii) Globally Aligned Orthogonal Quantization (GAOQ), which produces compact and predictable SID sequences by jointly reducing semantic ambiguity and prefix-conditional uncertainty. Theoretical analysis and extensive experiments across ten datasets show the effectiveness of ReSID. ReSID consistently outperforms strong sequential and SID-based generative baselines by an average of over 10%, while reducing tokenization cost by up to 122x. Code is available at https://github.com/FuCongResearchSquad/ReSID.
Reveal Hidden Pitfalls and Navigate Next Generation of Vector Similarity Search from Task-Centric Views
Dec 15, 2025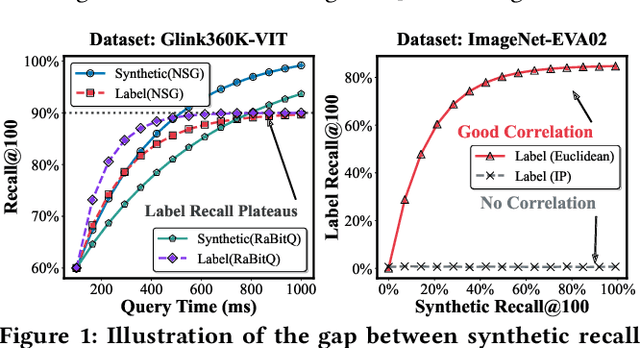

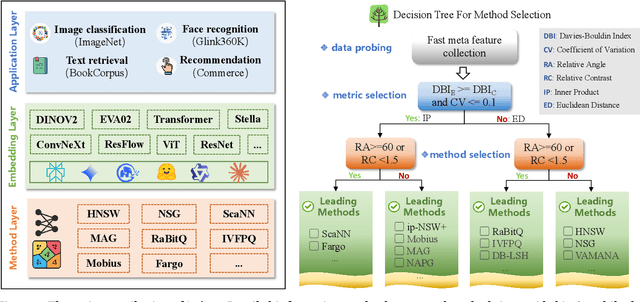
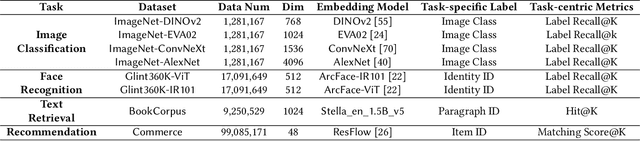
Abstract:Vector Similarity Search (VSS) in high-dimensional spaces is rapidly emerging as core functionality in next-generation database systems for numerous data-intensive services -- from embedding lookups in large language models (LLMs), to semantic information retrieval and recommendation engines. Current benchmarks, however, evaluate VSS primarily on the recall-latency trade-off against a ground truth defined solely by distance metrics, neglecting how retrieval quality ultimately impacts downstream tasks. This disconnect can mislead both academic research and industrial practice. We present Iceberg, a holistic benchmark suite for end-to-end evaluation of VSS methods in realistic application contexts. From a task-centric view, Iceberg uncovers the Information Loss Funnel, which identifies three principal sources of end-to-end performance degradation: (1) Embedding Loss during feature extraction; (2) Metric Misuse, where distances poorly reflect task relevance; (3) Data Distribution Sensitivity, highlighting index robustness across skews and modalities. For a more comprehensive assessment, Iceberg spans eight diverse datasets across key domains such as image classification, face recognition, text retrieval, and recommendation systems. Each dataset, ranging from 1M to 100M vectors, includes rich, task-specific labels and evaluation metrics, enabling assessment of retrieval algorithms within the full application pipeline rather than in isolation. Iceberg benchmarks 13 state-of-the-art VSS methods and re-ranks them based on application-level metrics, revealing substantial deviations from traditional rankings derived purely from recall-latency evaluations. Building on these insights, we define a set of task-centric meta-features and derive an interpretable decision tree to guide practitioners in selecting and tuning VSS methods for their specific workloads.
Tensor Decomposition Networks for Fast Machine Learning Interatomic Potential Computations
Jul 01, 2025Abstract:$\rm{SO}(3)$-equivariant networks are the dominant models for machine learning interatomic potentials (MLIPs). The key operation of such networks is the Clebsch-Gordan (CG) tensor product, which is computationally expensive. To accelerate the computation, we develop tensor decomposition networks (TDNs) as a class of approximately equivariant networks whose CG tensor products are replaced by low-rank tensor decompositions, such as the CANDECOMP/PARAFAC (CP) decomposition. With the CP decomposition, we prove (i) a uniform bound on the induced error of $\rm{SO}(3)$-equivariance, and (ii) the universality of approximating any equivariant bilinear map. To further reduce the number of parameters, we propose path-weight sharing that ties all multiplicity-space weights across the $O(L^3)$ CG paths into a single path without compromising equivariance, where $L$ is the maximum angular degree. The resulting layer acts as a plug-and-play replacement for tensor products in existing networks, and the computational complexity of tensor products is reduced from $O(L^6)$ to $O(L^4)$. We evaluate TDNs on PubChemQCR, a newly curated molecular relaxation dataset containing 105 million DFT-calculated snapshots. We also use existing datasets, including OC20, and OC22. Results show that TDNs achieve competitive performance with dramatic speedup in computations.
Embed Progressive Implicit Preference in Unified Space for Deep Collaborative Filtering
May 28, 2025Abstract:Embedding-based collaborative filtering, often coupled with nearest neighbor search, is widely deployed in large-scale recommender systems for personalized content selection. Modern systems leverage multiple implicit feedback signals (e.g., clicks, add to cart, purchases) to model user preferences comprehensively. However, prevailing approaches adopt a feedback-wise modeling paradigm, which (1) fails to capture the structured progression of user engagement entailed among different feedback and (2) embeds feedback-specific information into disjoint spaces, making representations incommensurable, increasing system complexity, and leading to suboptimal retrieval performance. A promising alternative is Ordinal Logistic Regression (OLR), which explicitly models discrete ordered relations. However, existing OLR-based recommendation models mainly focus on explicit feedback (e.g., movie ratings) and struggle with implicit, correlated feedback, where ordering is vague and non-linear. Moreover, standard OLR lacks flexibility in handling feedback-dependent covariates, resulting in suboptimal performance in real-world systems. To address these limitations, we propose Generalized Neural Ordinal Logistic Regression (GNOLR), which encodes multiple feature-feedback dependencies into a unified, structured embedding space and enforces feedback-specific dependency learning through a nested optimization framework. Thus, GNOLR enhances predictive accuracy, captures the progression of user engagement, and simplifies the retrieval process. We establish a theoretical comparison with existing paradigms, demonstrating how GNOLR avoids disjoint spaces while maintaining effectiveness. Extensive experiments on ten real-world datasets show that GNOLR significantly outperforms state-of-the-art methods in efficiency and adaptability.
Stitching Inner Product and Euclidean Metrics for Topology-aware Maximum Inner Product Search
Apr 21, 2025Abstract:Maximum Inner Product Search (MIPS) is a fundamental challenge in machine learning and information retrieval, particularly in high-dimensional data applications. Existing approaches to MIPS either rely solely on Inner Product (IP) similarity, which faces issues with local optima and redundant computations, or reduce the MIPS problem to the Nearest Neighbor Search under the Euclidean metric via space projection, leading to topology destruction and information loss. Despite the divergence of the two paradigms, we argue that there is no inherent binary opposition between IP and Euclidean metrics. By stitching IP and Euclidean in the design of indexing and search algorithms, we can significantly enhance MIPS performance. Specifically, this paper explores the theoretical and empirical connections between these two metrics from the MIPS perspective. Our investigation, grounded in graph-based search, reveals that different indexing and search strategies offer distinct advantages for MIPS, depending on the underlying data topology. Building on these insights, we introduce a novel graph-based index called Metric-Amphibious Graph (MAG) and a corresponding search algorithm, Adaptive Navigation with Metric Switch (ANMS). To facilitate parameter tuning for optimal performance, we identify three statistical indicators that capture essential data topology properties and correlate strongly with parameter tuning. Extensive experiments on 12 real-world datasets demonstrate that MAG outperforms existing state-of-the-art methods, achieving up to 4x search speedup while maintaining adaptability and scalability.
MedCT: A Clinical Terminology Graph for Generative AI Applications in Healthcare
Jan 11, 2025



Abstract:We introduce the world's first clinical terminology for the Chinese healthcare community, namely MedCT, accompanied by a clinical foundation model MedBERT and an entity linking model MedLink. The MedCT system enables standardized and programmable representation of Chinese clinical data, successively stimulating the development of new medicines, treatment pathways, and better patient outcomes for the populous Chinese community. Moreover, the MedCT knowledge graph provides a principled mechanism to minimize the hallucination problem of large language models (LLMs), therefore achieving significant levels of accuracy and safety in LLM-based clinical applications. By leveraging the LLMs' emergent capabilities of generativeness and expressiveness, we were able to rapidly built a production-quality terminology system and deployed to real-world clinical field within three months, while classical terminologies like SNOMED CT have gone through more than twenty years development. Our experiments show that the MedCT system achieves state-of-the-art (SOTA) performance in semantic matching and entity linking tasks, not only for Chinese but also for English. We also conducted a longitudinal field experiment by applying MedCT and LLMs in a representative spectrum of clinical tasks, including electronic health record (EHR) auto-generation and medical document search for diagnostic decision making. Our study shows a multitude of values of MedCT for clinical workflows and patient outcomes, especially in the new genre of clinical LLM applications. We present our approach in sufficient engineering detail, such that implementing a clinical terminology for other non-English societies should be readily reproducible. We openly release our terminology, models and algorithms, along with real-world clinical datasets for the development.
BioNeMo Framework: a modular, high-performance library for AI model development in drug discovery
Nov 15, 2024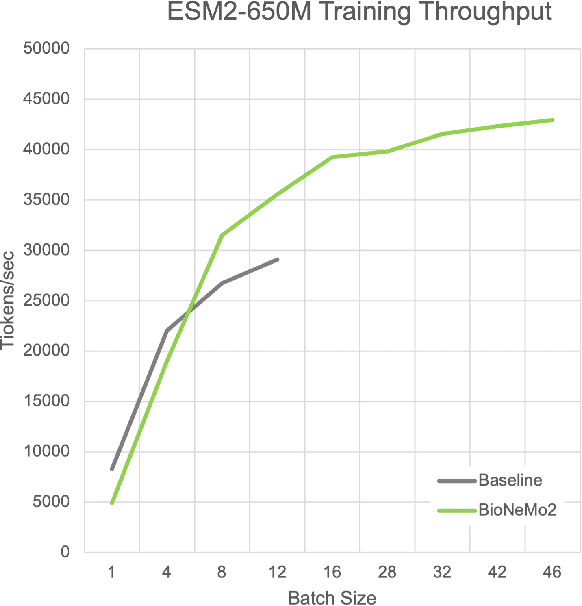
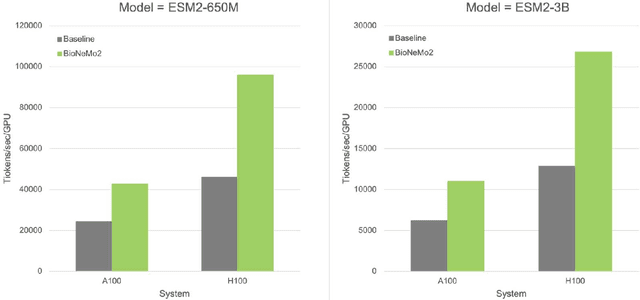
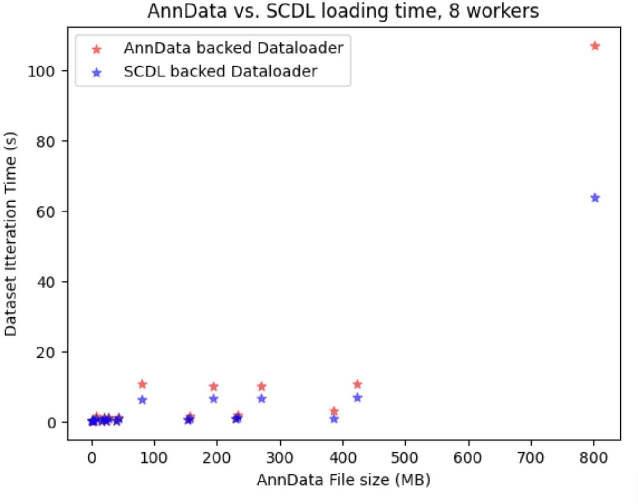
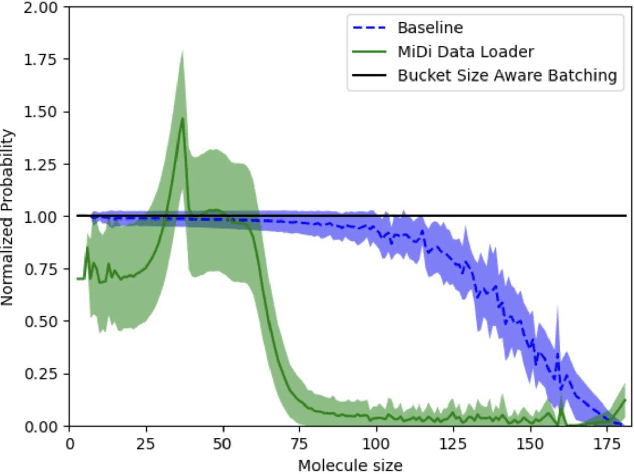
Abstract:Artificial Intelligence models encoding biology and chemistry are opening new routes to high-throughput and high-quality in-silico drug development. However, their training increasingly relies on computational scale, with recent protein language models (pLM) training on hundreds of graphical processing units (GPUs). We introduce the BioNeMo Framework to facilitate the training of computational biology and chemistry AI models across hundreds of GPUs. Its modular design allows the integration of individual components, such as data loaders, into existing workflows and is open to community contributions. We detail technical features of the BioNeMo Framework through use cases such as pLM pre-training and fine-tuning. On 256 NVIDIA A100s, BioNeMo Framework trains a three billion parameter BERT-based pLM on over one trillion tokens in 4.2 days. The BioNeMo Framework is open-source and free for everyone to use.
SineNet: Learning Temporal Dynamics in Time-Dependent Partial Differential Equations
Mar 28, 2024



Abstract:We consider using deep neural networks to solve time-dependent partial differential equations (PDEs), where multi-scale processing is crucial for modeling complex, time-evolving dynamics. While the U-Net architecture with skip connections is commonly used by prior studies to enable multi-scale processing, our analysis shows that the need for features to evolve across layers results in temporally misaligned features in skip connections, which limits the model's performance. To address this limitation, we propose SineNet, consisting of multiple sequentially connected U-shaped network blocks, referred to as waves. In SineNet, high-resolution features are evolved progressively through multiple stages, thereby reducing the amount of misalignment within each stage. We furthermore analyze the role of skip connections in enabling both parallel and sequential processing of multi-scale information. Our method is rigorously tested on multiple PDE datasets, including the Navier-Stokes equations and shallow water equations, showcasing the advantages of our proposed approach over conventional U-Nets with a comparable parameter budget. We further demonstrate that increasing the number of waves in SineNet while maintaining the same number of parameters leads to a monotonically improved performance. The results highlight the effectiveness of SineNet and the potential of our approach in advancing the state-of-the-art in neural PDE solver design. Our code is available as part of AIRS (https://github.com/divelab/AIRS).
Complete and Efficient Graph Transformers for Crystal Material Property Prediction
Mar 18, 2024Abstract:Crystal structures are characterized by atomic bases within a primitive unit cell that repeats along a regular lattice throughout 3D space. The periodic and infinite nature of crystals poses unique challenges for geometric graph representation learning. Specifically, constructing graphs that effectively capture the complete geometric information of crystals and handle chiral crystals remains an unsolved and challenging problem. In this paper, we introduce a novel approach that utilizes the periodic patterns of unit cells to establish the lattice-based representation for each atom, enabling efficient and expressive graph representations of crystals. Furthermore, we propose ComFormer, a SE(3) transformer designed specifically for crystalline materials. ComFormer includes two variants; namely, iComFormer that employs invariant geometric descriptors of Euclidean distances and angles, and eComFormer that utilizes equivariant vector representations. Experimental results demonstrate the state-of-the-art predictive accuracy of ComFormer variants on various tasks across three widely-used crystal benchmarks. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).
SoftTiger: A Clinical Foundation Model for Healthcare Workflows
Mar 01, 2024Abstract:We release and introduce SoftTiger, a clinical large language model (CLaM) designed as a foundation model for healthcare workflows. The narrative and unstructured nature of clinical notes is a major obstacle for healthcare intelligentization. We address a critical problem of structuring clinical notes into clinical data, according to international interoperability standards. We collect and annotate data for three critical subtasks, namely, international patient summary, clinical impression and medical encounter. We then supervised fine-tuned a state-of-the-art LLM using public and credentialed clinical data. The training is orchestrated in a way that the target model can first support basic clinical tasks such as abbreviation expansion and temporal information extraction, and then learn to perform more complex downstream clinical tasks such as impression and encounter summary. Moreover, we address, several modeling challenges in the healthcare context, e.g., extra long context window. Our blind pairwise evaluation shows that SoftTiger outperforms other popular open-source models and GPT-3.5, comparable to Gemini-pro, and only has a mild gap from GPT-4. We believe that LLMs may become a step-stone towards healthcare digitalization and democratization. Therefore, we publicly release SoftTiger models at scales of 13 billion and 70 billion parameters, as well as datasets and code for our innovative scalable evaluation, hopefully, making a significant contribution to the healthcare industry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge