Complete and Efficient Graph Transformers for Crystal Material Property Prediction

Crystal structures are characterized by atomic bases within a primitive unit cell that repeats along a regular lattice throughout 3D space. The periodic and infinite nature of crystals poses unique challenges for geometric graph representation learning. Specifically, constructing graphs that effectively capture the complete geometric information of crystals and handle chiral crystals remains an unsolved and challenging problem. In this paper, we introduce a novel approach that utilizes the periodic patterns of unit cells to establish the lattice-based representation for each atom, enabling efficient and expressive graph representations of crystals. Furthermore, we propose ComFormer, a SE(3) transformer designed specifically for crystalline materials. ComFormer includes two variants; namely, iComFormer that employs invariant geometric descriptors of Euclidean distances and angles, and eComFormer that utilizes equivariant vector representations. Experimental results demonstrate the state-of-the-art predictive accuracy of ComFormer variants on various tasks across three widely-used crystal benchmarks. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

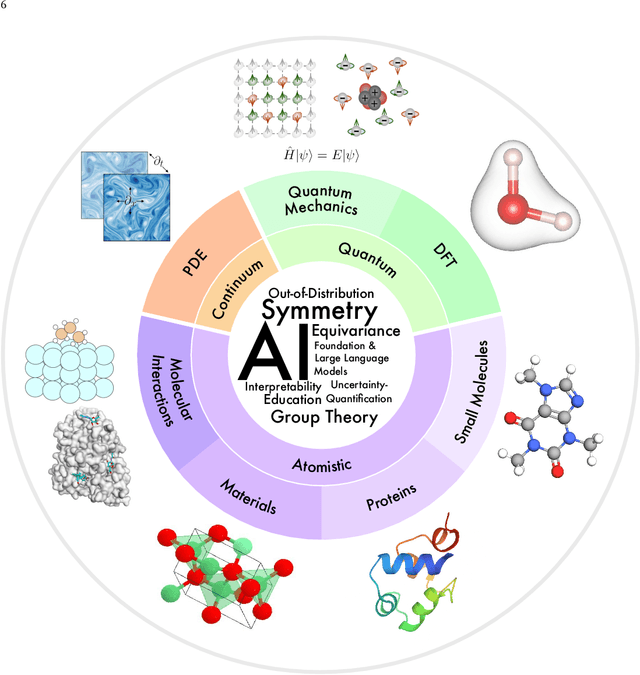
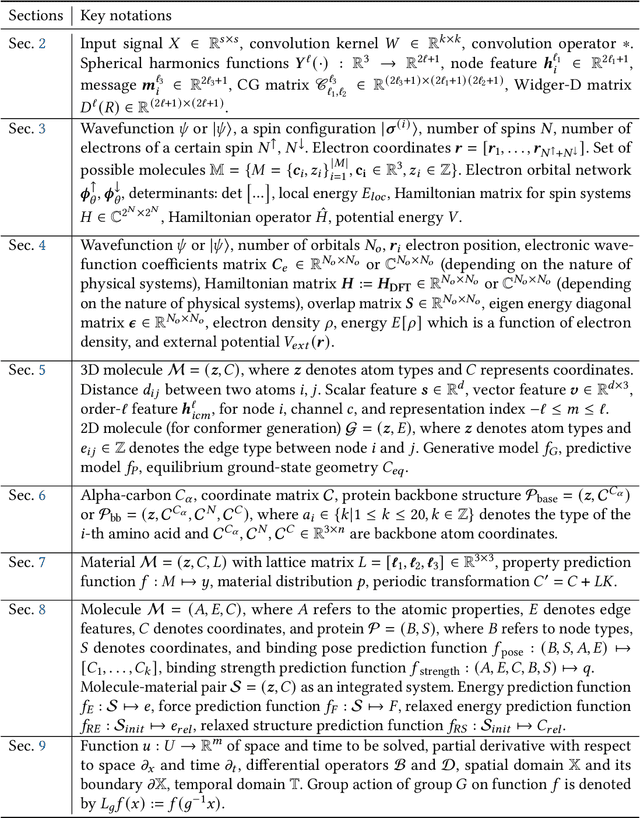
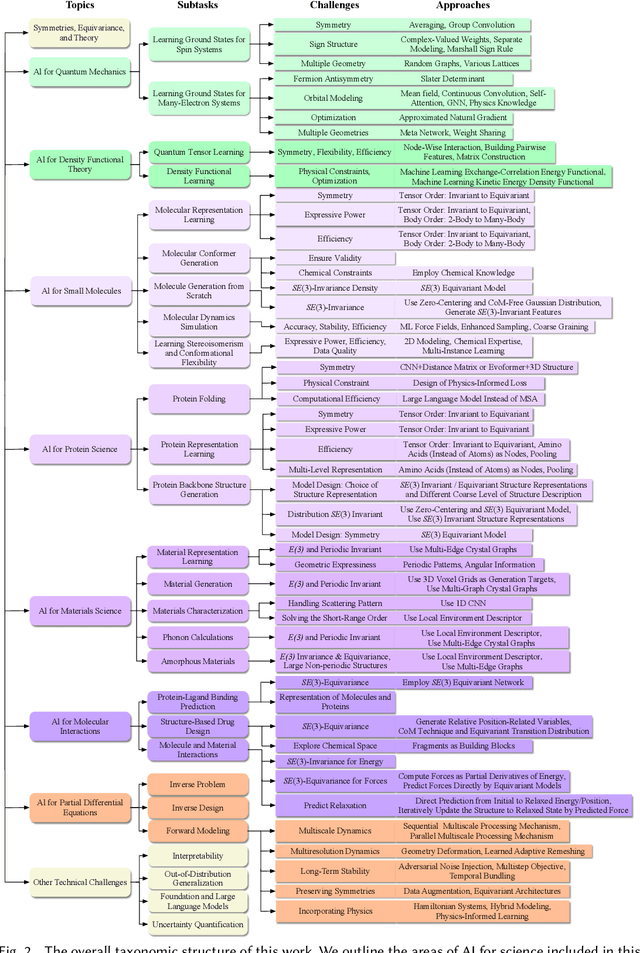
Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

Efficient Approximations of Complete Interatomic Potentials for Crystal Property Prediction

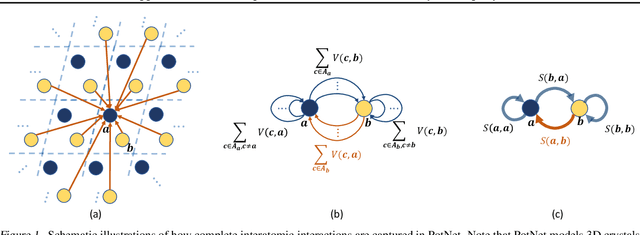
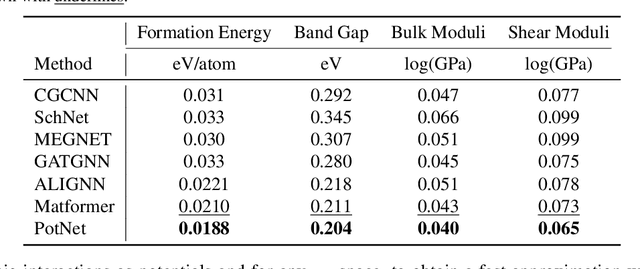
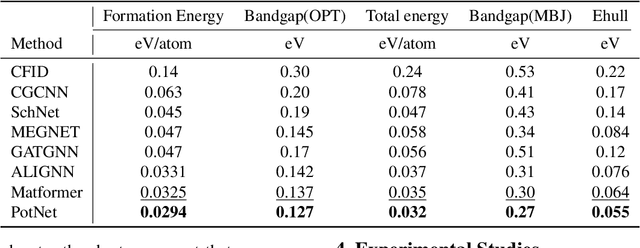
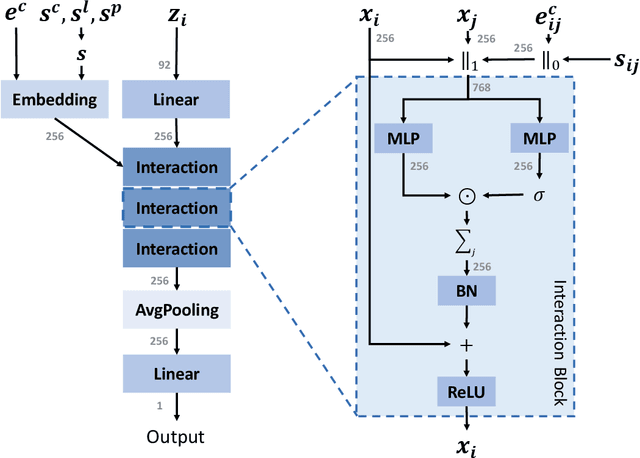
We study property prediction for crystal materials. A crystal structure consists of a minimal unit cell that is repeated infinitely in 3D space. How to accurately represent such repetitive structures in machine learning models remains unresolved. Current methods construct graphs by establishing edges only between nearby nodes, thereby failing to faithfully capture infinite repeating patterns and distant interatomic interactions. In this work, we propose several innovations to overcome these limitations. First, we propose to model physics-principled interatomic potentials directly instead of only using distances as in many existing methods. These potentials include the Coulomb potential, London dispersion potential, and Pauli repulsion potential. Second, we model the complete set of potentials among all atoms, instead of only between nearby atoms as in existing methods. This is enabled by our approximations of infinite potential summations with provable error bounds. We further develop efficient algorithms to compute the approximations. Finally, we propose to incorporate our computations of complete interatomic potentials into message passing neural networks for representation learning. We perform experiments on the JARVIS and Materials Project benchmarks for evaluation. Results show that the use of interatomic potentials and complete interatomic potentials leads to consistent performance improvements with reasonable computational costs. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS/tree/main/OpenMat/PotNet).

A Latent Diffusion Model for Protein Structure Generation

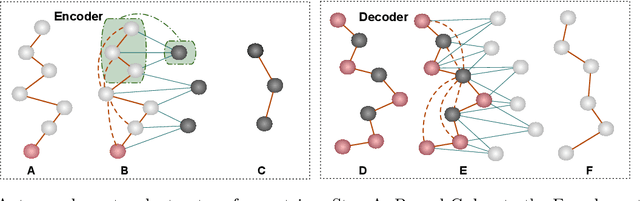
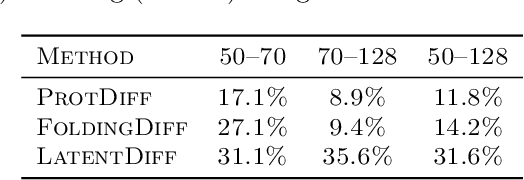
Proteins are complex biomolecules that perform a variety of crucial functions within living organisms. Designing and generating novel proteins can pave the way for many future synthetic biology applications, including drug discovery. However, it remains a challenging computational task due to the large modeling space of protein structures. In this study, we propose a latent diffusion model that can reduce the complexity of protein modeling while flexibly capturing the distribution of natural protein structures in a condensed latent space. Specifically, we propose an equivariant protein autoencoder that embeds proteins into a latent space and then uses an equivariant diffusion model to learn the distribution of the latent protein representations. Experimental results demonstrate that our method can effectively generate novel protein backbone structures with high designability and efficiency.

Periodic Graph Transformers for Crystal Material Property Prediction

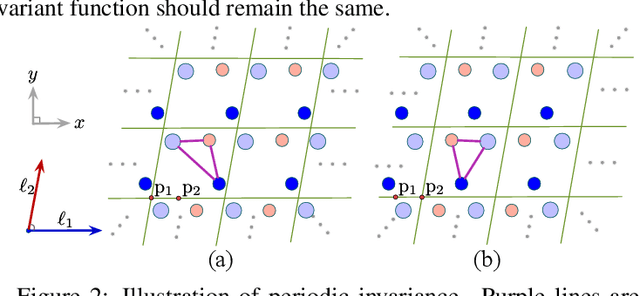
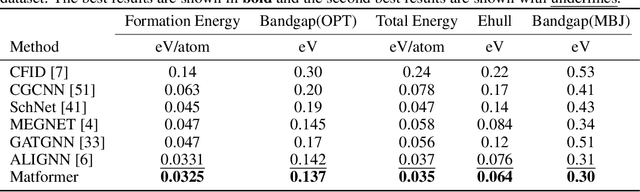
We consider representation learning on periodic graphs encoding crystal materials. Different from regular graphs, periodic graphs consist of a minimum unit cell repeating itself on a regular lattice in 3D space. How to effectively encode these periodic structures poses unique challenges not present in regular graph representation learning. In addition to being E(3) invariant, periodic graph representations need to be periodic invariant. That is, the learned representations should be invariant to shifts of cell boundaries as they are artificially imposed. Furthermore, the periodic repeating patterns need to be captured explicitly as lattices of different sizes and orientations may correspond to different materials. In this work, we propose a transformer architecture, known as Matformer, for periodic graph representation learning. Our Matformer is designed to be invariant to periodicity and can capture repeating patterns explicitly. In particular, Matformer encodes periodic patterns by efficient use of geometric distances between the same atoms in neighboring cells. Experimental results on multiple common benchmark datasets show that our Matformer outperforms baseline methods consistently. In addition, our results demonstrate the importance of periodic invariance and explicit repeating pattern encoding for crystal representation learning.

DIG: A Turnkey Library for Diving into Graph Deep Learning Research

Although there exist several libraries for deep learning on graphs, they are aiming at implementing basic operations for graph deep learning. In the research community, implementing and benchmarking various advanced tasks are still painful and time-consuming with existing libraries. To facilitate graph deep learning research, we introduce DIG: Dive into Graphs, a research-oriented library that integrates unified and extensible implementations of common graph deep learning algorithms for several advanced tasks. Currently, we consider graph generation, self-supervised learning on graphs, explainability of graph neural networks, and deep learning on 3D graphs. For each direction, we provide unified implementations of data interfaces, common algorithms, and evaluation metrics. Altogether, DIG is an extensible, open-source, and turnkey library for researchers to develop new methods and effortlessly compare with common baselines using widely used datasets and evaluation metrics. Source code and documentations are available at https://github.com/divelab/DIG/.

GraphDF: A Discrete Flow Model for Molecular Graph Generation

We consider the problem of molecular graph generation using deep models. While graphs are discrete, most existing methods use continuous latent variables, resulting in inaccurate modeling of discrete graph structures. In this work, we propose GraphDF, a novel discrete latent variable model for molecular graph generation based on normalizing flow methods. GraphDF uses invertible modulo shift transforms to map discrete latent variables to graph nodes and edges. We show that the use of discrete latent variables reduces computational costs and eliminates the negative effect of dequantization. Comprehensive experimental results show that GraphDF outperforms prior methods on random generation, property optimization, and constrained optimization tasks.

GraphEBM: Molecular Graph Generation with Energy-Based Models

Molecular graph generation is an emerging area of research with numerous applications. This problem remains challenging as molecular graphs are discrete, irregular, and permutation invariant to node order. Notably, most existing approaches fail to guarantee the intrinsic property of permutation invariance, resulting in unexpected bias in generative models. In this work, we propose GraphEBM to generate molecular graphs using energy-based models. In particular, we parameterize the energy function in a permutation invariant manner, thus making GraphEBM permutation invariant. We apply Langevin dynamics to train the energy function by approximately maximizing likelihood and generate samples with low energies. Furthermore, to generate molecules with a specific desirable property, we propose a simple yet effective strategy, which pushes down energies with flexible degrees according to the properties of corresponding molecules. Finally, we explore the use of GraphEBM for generating molecules with multiple objectives in a compositional manner. Comprehensive experimental results on random, goal-directed, and compositional generation tasks demonstrate the effectiveness of our proposed method.