Curriculum Reinforcement Learning from Easy to Hard Tasks Improves LLM Reasoning

We aim to improve the reasoning capabilities of language models via reinforcement learning (RL). Recent RL post-trained models like DeepSeek-R1 have demonstrated reasoning abilities on mathematical and coding tasks. However, prior studies suggest that using RL alone to improve reasoning on inherently difficult tasks is less effective. Here, we draw inspiration from curriculum learning and propose to schedule tasks from easy to hard (E2H), allowing LLMs to build reasoning skills gradually. Our method is termed E2H Reasoner. Empirically, we observe that, although easy tasks are important initially, fading them out through appropriate scheduling is essential in preventing overfitting. Theoretically, we establish convergence guarantees for E2H Reasoner within an approximate policy iteration framework. We derive finite-sample complexity bounds and show that when tasks are appropriately decomposed and conditioned, learning through curriculum stages requires fewer total samples than direct learning. Experiments across multiple domains show that E2H Reasoner significantly improves the reasoning ability of small LLMs (1.5B to 3B), which otherwise struggle when trained with vanilla RL alone, highlighting the effectiveness of our method.

Discovering Physics Laws of Dynamical Systems via Invariant Function Learning

We consider learning underlying laws of dynamical systems governed by ordinary differential equations (ODE). A key challenge is how to discover intrinsic dynamics across multiple environments while circumventing environment-specific mechanisms. Unlike prior work, we tackle more complex environments where changes extend beyond function coefficients to entirely different function forms. For example, we demonstrate the discovery of ideal pendulum's natural motion $\alpha^2 \sin{\theta_t}$ by observing pendulum dynamics in different environments, such as the damped environment $\alpha^2 \sin(\theta_t) - \rho \omega_t$ and powered environment $\alpha^2 \sin(\theta_t) + \rho \frac{\omega_t}{\left|\omega_t\right|}$. Here, we formulate this problem as an \emph{invariant function learning} task and propose a new method, known as \textbf{D}isentanglement of \textbf{I}nvariant \textbf{F}unctions (DIF), that is grounded in causal analysis. We propose a causal graph and design an encoder-decoder hypernetwork that explicitly disentangles invariant functions from environment-specific dynamics. The discovery of invariant functions is guaranteed by our information-based principle that enforces the independence between extracted invariant functions and environments. Quantitative comparisons with meta-learning and invariant learning baselines on three ODE systems demonstrate the effectiveness and efficiency of our method. Furthermore, symbolic regression explanation results highlight the ability of our framework to uncover intrinsic laws.

A Hierarchical Language Model For Interpretable Graph Reasoning

Large language models (LLMs) are being increasingly explored for graph tasks. Despite their remarkable success in text-based tasks, LLMs' capabilities in understanding explicit graph structures remain limited, particularly with large graphs. In this work, we introduce Hierarchical Language Model for Graph (HLM-G), which employs a two-block architecture to capture node-centric local information and interaction-centric global structure, effectively enhancing graph structure understanding abilities. The proposed scheme allows LLMs to address various graph queries with high efficacy, efficiency, and robustness, while reducing computational costs on large-scale graph tasks. Furthermore, we demonstrate the interpretability of our model using intrinsic attention weights and established explainers. Comprehensive evaluations across diverse graph reasoning and real-world tasks of node, link, and graph-levels highlight the superiority of our method, marking a significant advancement in the application of LLMs to graph understanding.

Geometry Informed Tokenization of Molecules for Language Model Generation

We consider molecule generation in 3D space using language models (LMs), which requires discrete tokenization of 3D molecular geometries. Although tokenization of molecular graphs exists, that for 3D geometries is largely unexplored. Here, we attempt to bridge this gap by proposing the Geo2Seq, which converts molecular geometries into $SE(3)$-invariant 1D discrete sequences. Geo2Seq consists of canonical labeling and invariant spherical representation steps, which together maintain geometric and atomic fidelity in a format conducive to LMs. Our experiments show that, when coupled with Geo2Seq, various LMs excel in molecular geometry generation, especially in controlled generation tasks.

Equivariance via Minimal Frame Averaging for More Symmetries and Efficiency

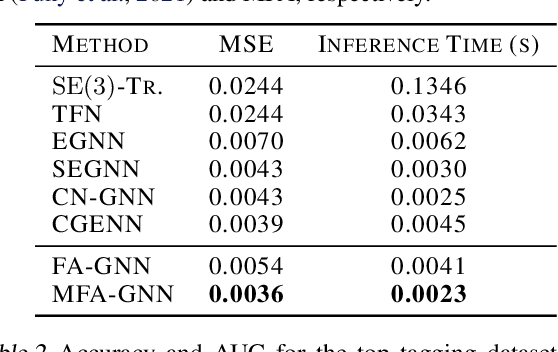
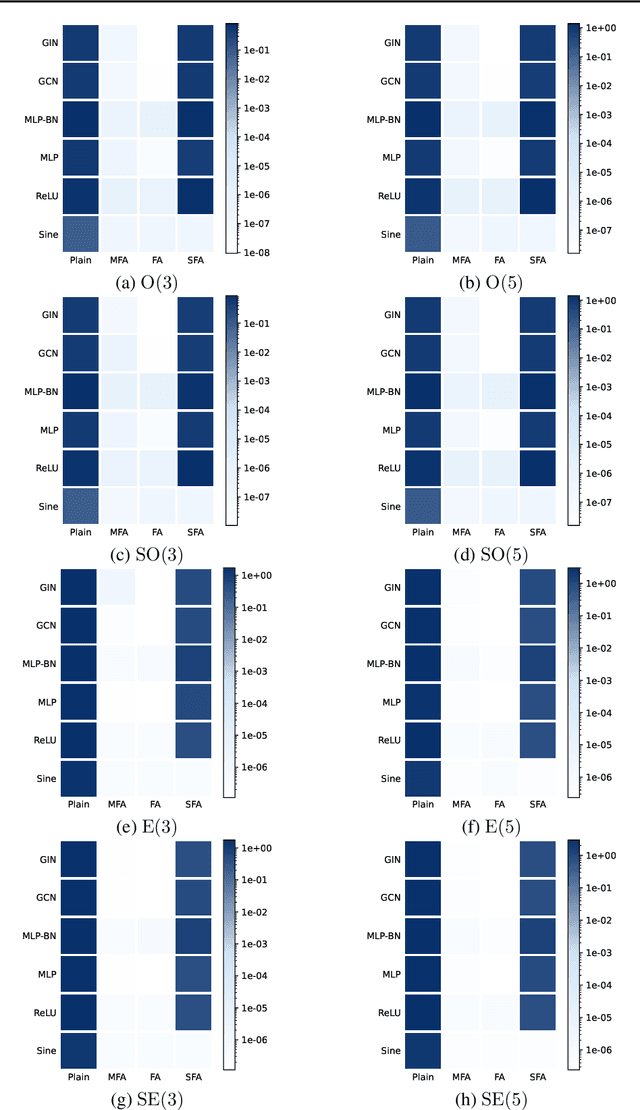
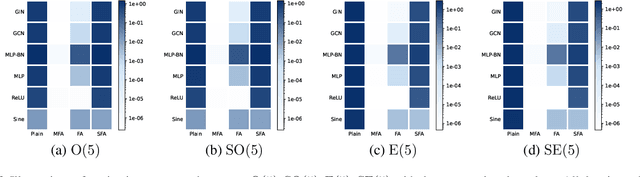
We consider achieving equivariance in machine learning systems via frame averaging. Current frame averaging methods involve a costly sum over large frames or rely on sampling-based approaches that only yield approximate equivariance. Here, we propose Minimal Frame Averaging (MFA), a mathematical framework for constructing provably minimal frames that are exactly equivariant. The general foundations of MFA also allow us to extend frame averaging to more groups than previously considered, including the Lorentz group for describing symmetries in space-time, and the unitary group for complex-valued domains. Results demonstrate the efficiency and effectiveness of encoding symmetries via MFA across a diverse range of tasks, including $n$-body simulation, top tagging in collider physics, and relaxed energy prediction. Our code is available at https://github.com/divelab/MFA.

Active Test-Time Adaptation: Theoretical Analyses and An Algorithm

Test-time adaptation (TTA) addresses distribution shifts for streaming test data in unsupervised settings. Currently, most TTA methods can only deal with minor shifts and rely heavily on heuristic and empirical studies. To advance TTA under domain shifts, we propose the novel problem setting of active test-time adaptation (ATTA) that integrates active learning within the fully TTA setting. We provide a learning theory analysis, demonstrating that incorporating limited labeled test instances enhances overall performances across test domains with a theoretical guarantee. We also present a sample entropy balancing for implementing ATTA while avoiding catastrophic forgetting (CF). We introduce a simple yet effective ATTA algorithm, known as SimATTA, using real-time sample selection techniques. Extensive experimental results confirm consistency with our theoretical analyses and show that the proposed ATTA method yields substantial performance improvements over TTA methods while maintaining efficiency and shares similar effectiveness to the more demanding active domain adaptation (ADA) methods. Our code is available at https://github.com/divelab/ATTA

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

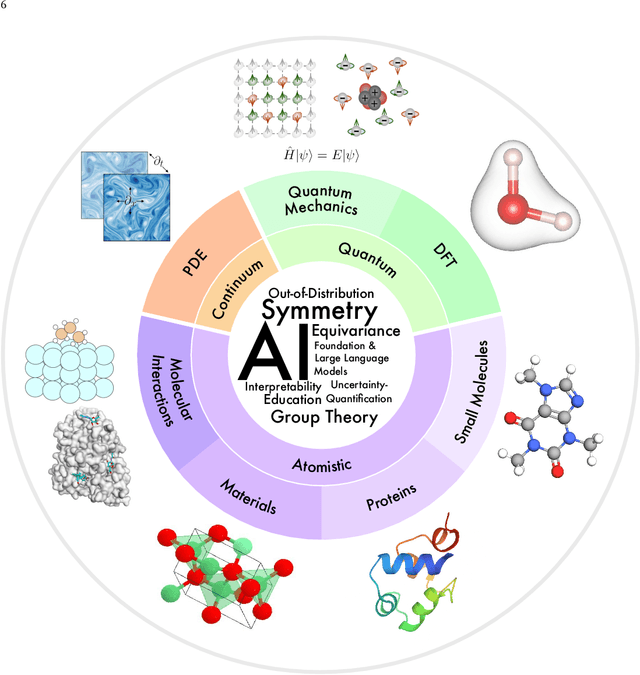
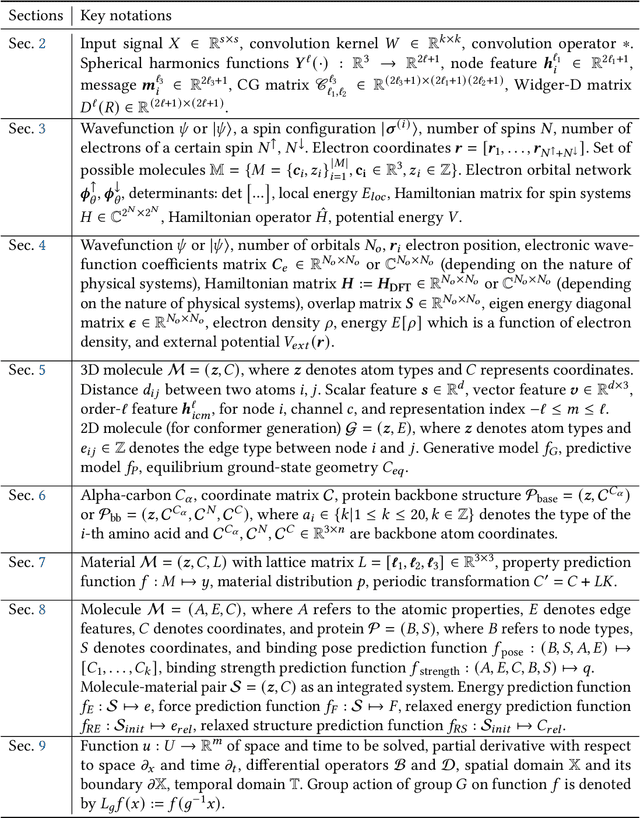
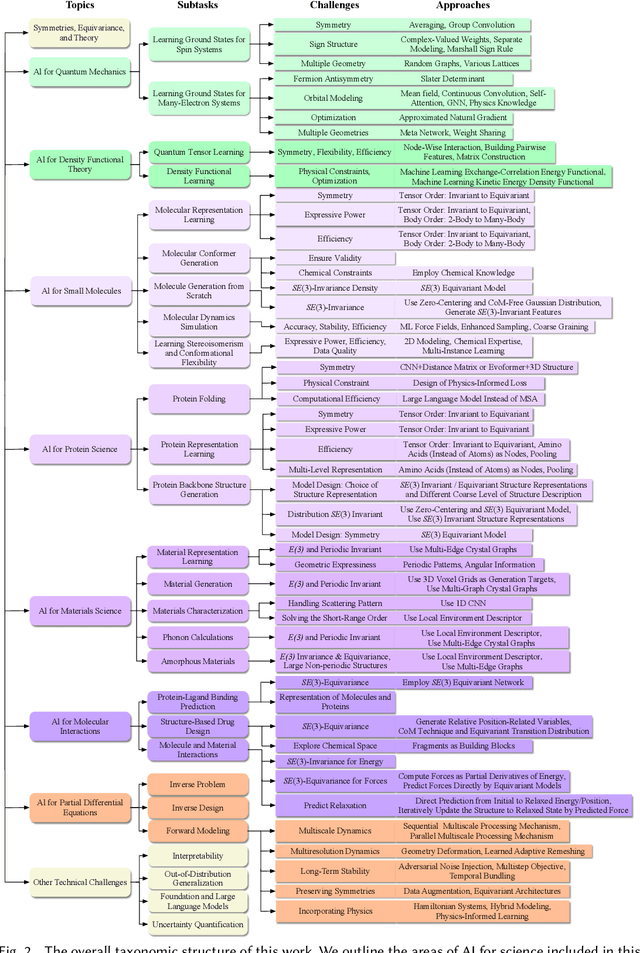
Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

Graph Structure and Feature Extrapolation for Out-of-Distribution Generalization

Out-of-distribution (OOD) generalization deals with the prevalent learning scenario where test distribution shifts from training distribution. With rising application demands and inherent complexity, graph OOD problems call for specialized solutions. While data-centric methods exhibit performance enhancements on many generic machine learning tasks, there is a notable absence of data augmentation methods tailored for graph OOD generalization. In this work, we propose to achieve graph OOD generalization with the novel design of non-Euclidean-space linear extrapolation. The proposed augmentation strategy extrapolates both structure and feature spaces to generate OOD graph data. Our design tailors OOD samples for specific shifts without corrupting underlying causal mechanisms. Theoretical analysis and empirical results evidence the effectiveness of our method in solving target shifts, showing substantial and constant improvements across various graph OOD tasks.

Joint Learning of Label and Environment Causal Independence for Graph Out-of-Distribution Generalization

We tackle the problem of graph out-of-distribution (OOD) generalization. Existing graph OOD algorithms either rely on restricted assumptions or fail to exploit environment information in training data. In this work, we propose to simultaneously incorporate label and environment causal independence (LECI) to fully make use of label and environment information, thereby addressing the challenges faced by prior methods on identifying causal and invariant subgraphs. We further develop an adversarial training strategy to jointly optimize these two properties for causal subgraph discovery with theoretical guarantees. Extensive experiments and analysis show that LECI significantly outperforms prior methods on both synthetic and real-world datasets, establishing LECI as a practical and effective solution for graph OOD generalization.

FlowX: Towards Explainable Graph Neural Networks via Message Flows

We investigate the explainability of graph neural networks (GNNs) as a step towards elucidating their working mechanisms. While most current methods focus on explaining graph nodes, edges, or features, we argue that, as the inherent functional mechanism of GNNs, message flows are more natural for performing explainability. To this end, we propose a novel method here, known as FlowX, to explain GNNs by identifying important message flows. To quantify the importance of flows, we propose to follow the philosophy of Shapley values from cooperative game theory. To tackle the complexity of computing all coalitions' marginal contributions, we propose an approximation scheme to compute Shapley-like values as initial assessments of further redistribution training. We then propose a learning algorithm to train flow scores and improve explainability. Experimental studies on both synthetic and real-world datasets demonstrate that our proposed FlowX leads to improved explainability of GNNs.