Yuchao Lin
Tensor Decomposition Networks for Fast Machine Learning Interatomic Potential Computations
Jul 01, 2025Abstract:$\rm{SO}(3)$-equivariant networks are the dominant models for machine learning interatomic potentials (MLIPs). The key operation of such networks is the Clebsch-Gordan (CG) tensor product, which is computationally expensive. To accelerate the computation, we develop tensor decomposition networks (TDNs) as a class of approximately equivariant networks whose CG tensor products are replaced by low-rank tensor decompositions, such as the CANDECOMP/PARAFAC (CP) decomposition. With the CP decomposition, we prove (i) a uniform bound on the induced error of $\rm{SO}(3)$-equivariance, and (ii) the universality of approximating any equivariant bilinear map. To further reduce the number of parameters, we propose path-weight sharing that ties all multiplicity-space weights across the $O(L^3)$ CG paths into a single path without compromising equivariance, where $L$ is the maximum angular degree. The resulting layer acts as a plug-and-play replacement for tensor products in existing networks, and the computational complexity of tensor products is reduced from $O(L^6)$ to $O(L^4)$. We evaluate TDNs on PubChemQCR, a newly curated molecular relaxation dataset containing 105 million DFT-calculated snapshots. We also use existing datasets, including OC20, and OC22. Results show that TDNs achieve competitive performance with dramatic speedup in computations.
Efficient Prediction of SO(3)-Equivariant Hamiltonian Matrices via SO(2) Local Frames
Jun 11, 2025Abstract:We consider the task of predicting Hamiltonian matrices to accelerate electronic structure calculations, which plays an important role in physics, chemistry, and materials science. Motivated by the inherent relationship between the off-diagonal blocks of the Hamiltonian matrix and the SO(2) local frame, we propose a novel and efficient network, called QHNetV2, that achieves global SO(3) equivariance without the costly SO(3) Clebsch-Gordan tensor products. This is achieved by introducing a set of new efficient and powerful SO(2)-equivariant operations and performing all off-diagonal feature updates and message passing within SO(2) local frames, thereby eliminating the need of SO(3) tensor products. Moreover, a continuous SO(2) tensor product is performed within the SO(2) local frame at each node to fuse node features, mimicking the symmetric contraction operation. Extensive experiments on the large QH9 and MD17 datasets demonstrate that our model achieves superior performance across a wide range of molecular structures and trajectories, highlighting its strong generalization capability. The proposed SO(2) operations on SO(2) local frames offer a promising direction for scalable and symmetry-aware learning of electronic structures. Our code will be released as part of the AIRS library https://github.com/divelab/AIRS.
A Two-Phase Deep Learning Framework for Adaptive Time-Stepping in High-Speed Flow Modeling
Jun 09, 2025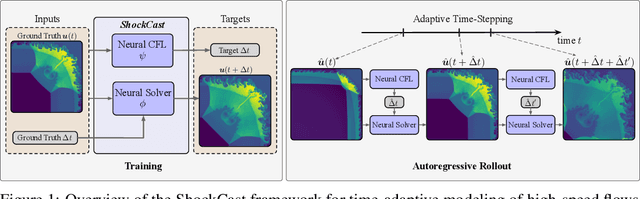

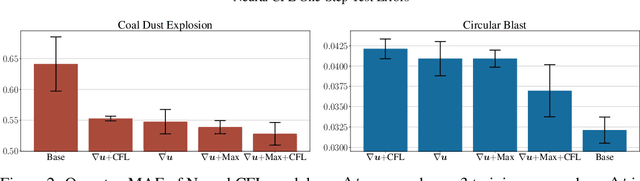
Abstract:We consider the problem of modeling high-speed flows using machine learning methods. While most prior studies focus on low-speed fluid flows in which uniform time-stepping is practical, flows approaching and exceeding the speed of sound exhibit sudden changes such as shock waves. In such cases, it is essential to use adaptive time-stepping methods to allow a temporal resolution sufficient to resolve these phenomena while simultaneously balancing computational costs. Here, we propose a two-phase machine learning method, known as ShockCast, to model high-speed flows with adaptive time-stepping. In the first phase, we propose to employ a machine learning model to predict the timestep size. In the second phase, the predicted timestep is used as an input along with the current fluid fields to advance the system state by the predicted timestep. We explore several physically-motivated components for timestep prediction and introduce timestep conditioning strategies inspired by neural ODE and Mixture of Experts. As ShockCast is the first framework for learning high-speed flows, we evaluate our methods by generating two supersonic flow datasets, available at https://huggingface.co/datasets/divelab. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).
Geometry Informed Tokenization of Molecules for Language Model Generation
Aug 19, 2024Abstract:We consider molecule generation in 3D space using language models (LMs), which requires discrete tokenization of 3D molecular geometries. Although tokenization of molecular graphs exists, that for 3D geometries is largely unexplored. Here, we attempt to bridge this gap by proposing the Geo2Seq, which converts molecular geometries into $SE(3)$-invariant 1D discrete sequences. Geo2Seq consists of canonical labeling and invariant spherical representation steps, which together maintain geometric and atomic fidelity in a format conducive to LMs. Our experiments show that, when coupled with Geo2Seq, various LMs excel in molecular geometry generation, especially in controlled generation tasks.
Equivariance via Minimal Frame Averaging for More Symmetries and Efficiency
Jun 11, 2024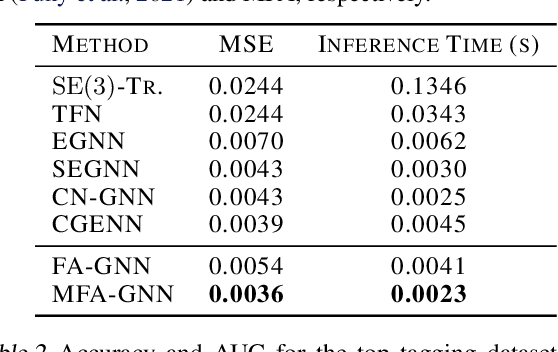
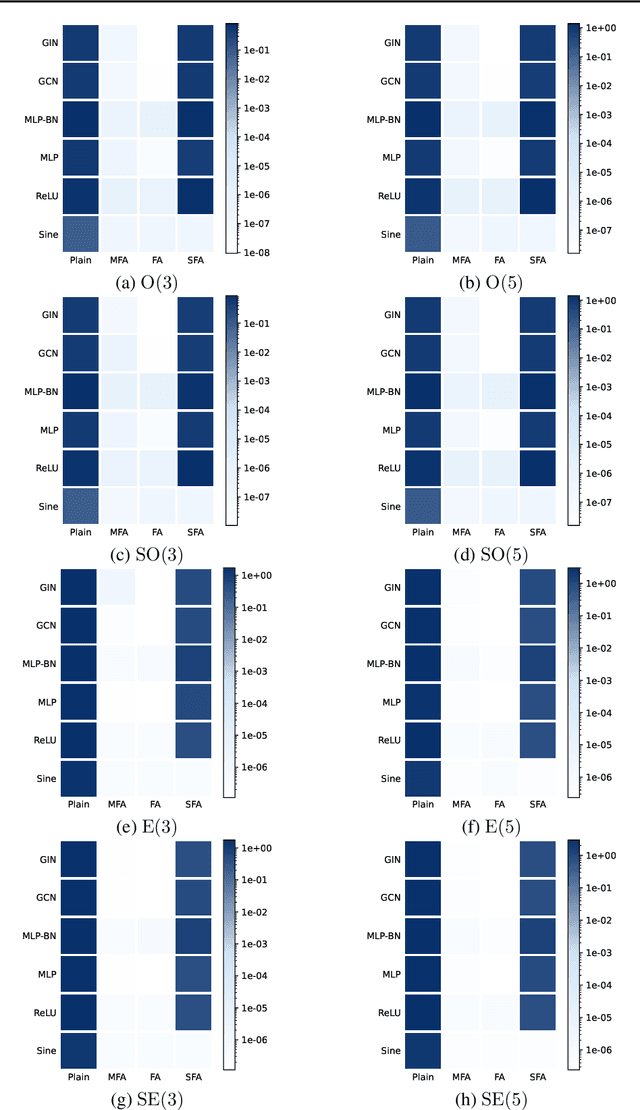

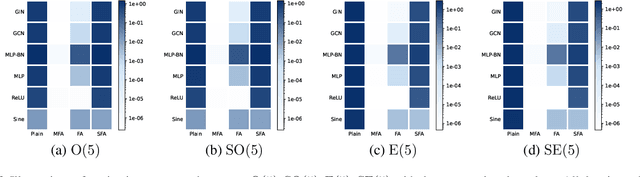
Abstract:We consider achieving equivariance in machine learning systems via frame averaging. Current frame averaging methods involve a costly sum over large frames or rely on sampling-based approaches that only yield approximate equivariance. Here, we propose Minimal Frame Averaging (MFA), a mathematical framework for constructing provably minimal frames that are exactly equivariant. The general foundations of MFA also allow us to extend frame averaging to more groups than previously considered, including the Lorentz group for describing symmetries in space-time, and the unitary group for complex-valued domains. Results demonstrate the efficiency and effectiveness of encoding symmetries via MFA across a diverse range of tasks, including $n$-body simulation, top tagging in collider physics, and relaxed energy prediction. Our code is available at https://github.com/divelab/MFA.
SineNet: Learning Temporal Dynamics in Time-Dependent Partial Differential Equations
Mar 28, 2024



Abstract:We consider using deep neural networks to solve time-dependent partial differential equations (PDEs), where multi-scale processing is crucial for modeling complex, time-evolving dynamics. While the U-Net architecture with skip connections is commonly used by prior studies to enable multi-scale processing, our analysis shows that the need for features to evolve across layers results in temporally misaligned features in skip connections, which limits the model's performance. To address this limitation, we propose SineNet, consisting of multiple sequentially connected U-shaped network blocks, referred to as waves. In SineNet, high-resolution features are evolved progressively through multiple stages, thereby reducing the amount of misalignment within each stage. We furthermore analyze the role of skip connections in enabling both parallel and sequential processing of multi-scale information. Our method is rigorously tested on multiple PDE datasets, including the Navier-Stokes equations and shallow water equations, showcasing the advantages of our proposed approach over conventional U-Nets with a comparable parameter budget. We further demonstrate that increasing the number of waves in SineNet while maintaining the same number of parameters leads to a monotonically improved performance. The results highlight the effectiveness of SineNet and the potential of our approach in advancing the state-of-the-art in neural PDE solver design. Our code is available as part of AIRS (https://github.com/divelab/AIRS).
Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems
Jul 17, 2023
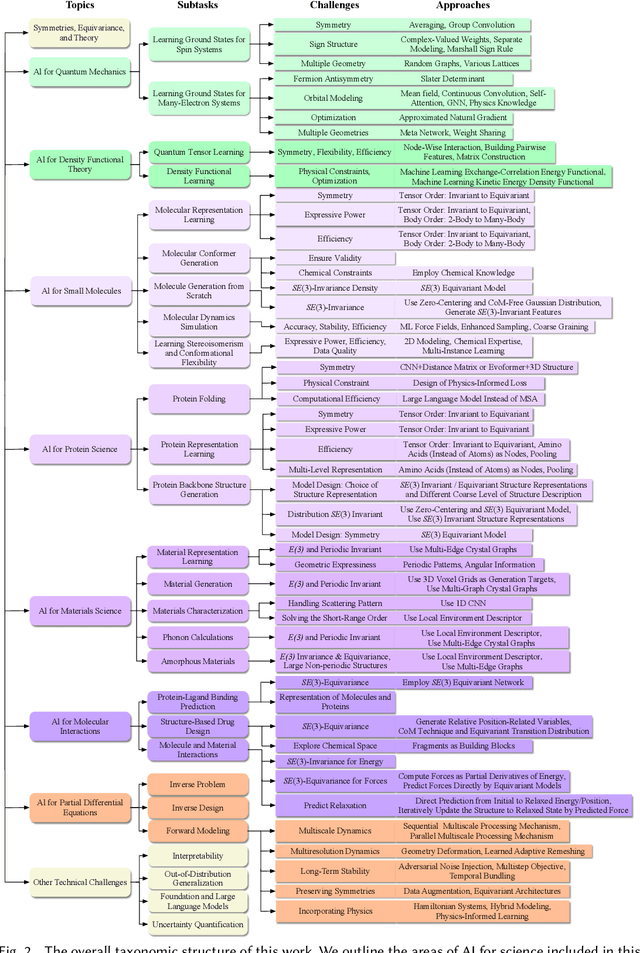

Abstract:Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.
Efficient Approximations of Complete Interatomic Potentials for Crystal Property Prediction
Jun 26, 2023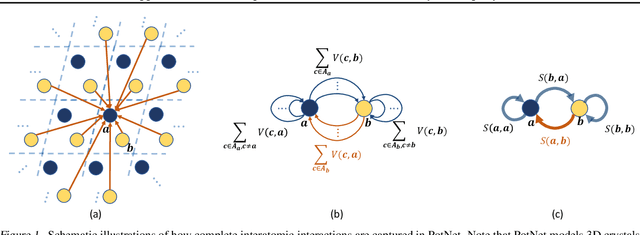
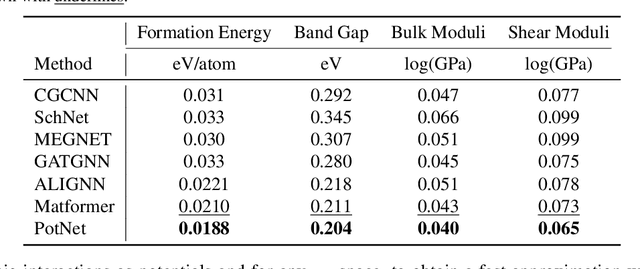
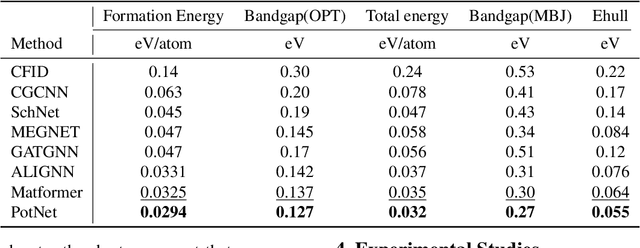
Abstract:We study property prediction for crystal materials. A crystal structure consists of a minimal unit cell that is repeated infinitely in 3D space. How to accurately represent such repetitive structures in machine learning models remains unresolved. Current methods construct graphs by establishing edges only between nearby nodes, thereby failing to faithfully capture infinite repeating patterns and distant interatomic interactions. In this work, we propose several innovations to overcome these limitations. First, we propose to model physics-principled interatomic potentials directly instead of only using distances as in many existing methods. These potentials include the Coulomb potential, London dispersion potential, and Pauli repulsion potential. Second, we model the complete set of potentials among all atoms, instead of only between nearby atoms as in existing methods. This is enabled by our approximations of infinite potential summations with provable error bounds. We further develop efficient algorithms to compute the approximations. Finally, we propose to incorporate our computations of complete interatomic potentials into message passing neural networks for representation learning. We perform experiments on the JARVIS and Materials Project benchmarks for evaluation. Results show that the use of interatomic potentials and complete interatomic potentials leads to consistent performance improvements with reasonable computational costs. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS/tree/main/OpenMat/PotNet).
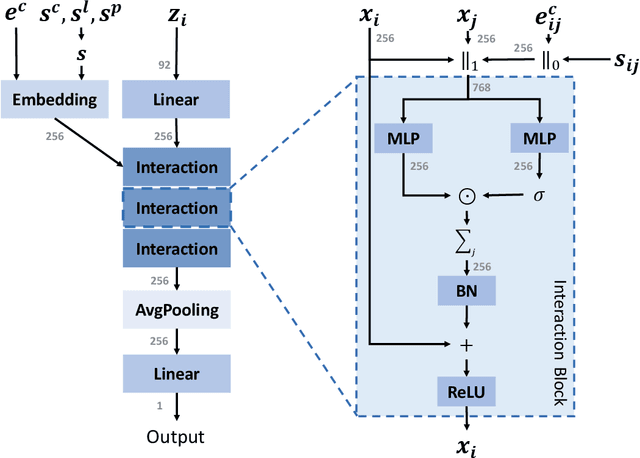
Periodic Graph Transformers for Crystal Material Property Prediction
Sep 23, 2022

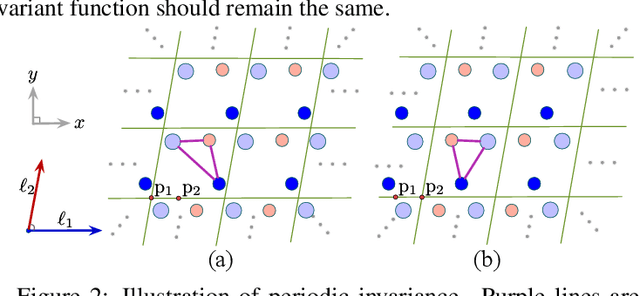
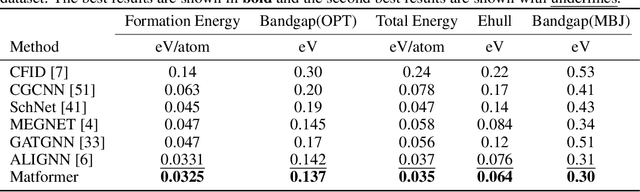
Abstract:We consider representation learning on periodic graphs encoding crystal materials. Different from regular graphs, periodic graphs consist of a minimum unit cell repeating itself on a regular lattice in 3D space. How to effectively encode these periodic structures poses unique challenges not present in regular graph representation learning. In addition to being E(3) invariant, periodic graph representations need to be periodic invariant. That is, the learned representations should be invariant to shifts of cell boundaries as they are artificially imposed. Furthermore, the periodic repeating patterns need to be captured explicitly as lattices of different sizes and orientations may correspond to different materials. In this work, we propose a transformer architecture, known as Matformer, for periodic graph representation learning. Our Matformer is designed to be invariant to periodicity and can capture repeating patterns explicitly. In particular, Matformer encodes periodic patterns by efficient use of geometric distances between the same atoms in neighboring cells. Experimental results on multiple common benchmark datasets show that our Matformer outperforms baseline methods consistently. In addition, our results demonstrate the importance of periodic invariance and explicit repeating pattern encoding for crystal representation learning.
ComENet: Towards Complete and Efficient Message Passing for 3D Molecular Graphs
Jun 17, 2022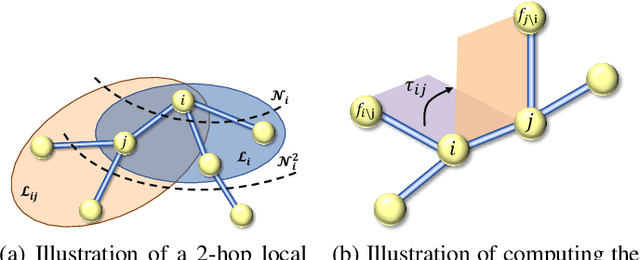

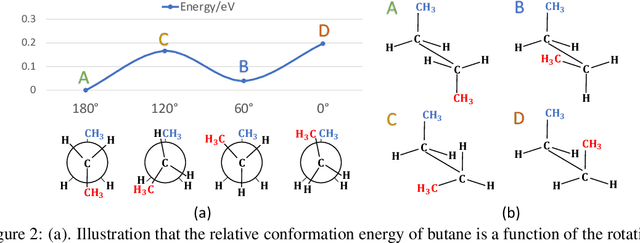

Abstract:Many real-world data can be modeled as 3D graphs, but learning representations that incorporates 3D information completely and efficiently is challenging. Existing methods either use partial 3D information, or suffer from excessive computational cost. To incorporate 3D information completely and efficiently, we propose a novel message passing scheme that operates within 1-hop neighborhood. Our method guarantees full completeness of 3D information on 3D graphs by achieving global and local completeness. Notably, we propose the important rotation angles to fulfill global completeness. Additionally, we show that our method is orders of magnitude faster than prior methods. We provide rigorous proof of completeness and analysis of time complexity for our methods. As molecules are in essence quantum systems, we build the \underline{com}plete and \underline{e}fficient graph neural network (ComENet) by combing quantum inspired basis functions and the proposed message passing scheme. Experimental results demonstrate the capability and efficiency of ComENet, especially on real-world datasets that are large in both numbers and sizes of graphs. Our code is publicly available as part of the DIG library (\url{https://github.com/divelab/DIG}).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge