Xiaofeng Qian
Tensor Decomposition Networks for Fast Machine Learning Interatomic Potential Computations
Jul 01, 2025Abstract:$\rm{SO}(3)$-equivariant networks are the dominant models for machine learning interatomic potentials (MLIPs). The key operation of such networks is the Clebsch-Gordan (CG) tensor product, which is computationally expensive. To accelerate the computation, we develop tensor decomposition networks (TDNs) as a class of approximately equivariant networks whose CG tensor products are replaced by low-rank tensor decompositions, such as the CANDECOMP/PARAFAC (CP) decomposition. With the CP decomposition, we prove (i) a uniform bound on the induced error of $\rm{SO}(3)$-equivariance, and (ii) the universality of approximating any equivariant bilinear map. To further reduce the number of parameters, we propose path-weight sharing that ties all multiplicity-space weights across the $O(L^3)$ CG paths into a single path without compromising equivariance, where $L$ is the maximum angular degree. The resulting layer acts as a plug-and-play replacement for tensor products in existing networks, and the computational complexity of tensor products is reduced from $O(L^6)$ to $O(L^4)$. We evaluate TDNs on PubChemQCR, a newly curated molecular relaxation dataset containing 105 million DFT-calculated snapshots. We also use existing datasets, including OC20, and OC22. Results show that TDNs achieve competitive performance with dramatic speedup in computations.
Efficient Prediction of SO(3)-Equivariant Hamiltonian Matrices via SO(2) Local Frames
Jun 11, 2025Abstract:We consider the task of predicting Hamiltonian matrices to accelerate electronic structure calculations, which plays an important role in physics, chemistry, and materials science. Motivated by the inherent relationship between the off-diagonal blocks of the Hamiltonian matrix and the SO(2) local frame, we propose a novel and efficient network, called QHNetV2, that achieves global SO(3) equivariance without the costly SO(3) Clebsch-Gordan tensor products. This is achieved by introducing a set of new efficient and powerful SO(2)-equivariant operations and performing all off-diagonal feature updates and message passing within SO(2) local frames, thereby eliminating the need of SO(3) tensor products. Moreover, a continuous SO(2) tensor product is performed within the SO(2) local frame at each node to fuse node features, mimicking the symmetric contraction operation. Extensive experiments on the large QH9 and MD17 datasets demonstrate that our model achieves superior performance across a wide range of molecular structures and trajectories, highlighting its strong generalization capability. The proposed SO(2) operations on SO(2) local frames offer a promising direction for scalable and symmetry-aware learning of electronic structures. Our code will be released as part of the AIRS library https://github.com/divelab/AIRS.
Toward Greater Autonomy in Materials Discovery Agents: Unifying Planning, Physics, and Scientists
Jun 05, 2025Abstract:We aim at designing language agents with greater autonomy for crystal materials discovery. While most of existing studies restrict the agents to perform specific tasks within predefined workflows, we aim to automate workflow planning given high-level goals and scientist intuition. To this end, we propose Materials Agent unifying Planning, Physics, and Scientists, known as MAPPS. MAPPS consists of a Workflow Planner, a Tool Code Generator, and a Scientific Mediator. The Workflow Planner uses large language models (LLMs) to generate structured and multi-step workflows. The Tool Code Generator synthesizes executable Python code for various tasks, including invoking a force field foundation model that encodes physics. The Scientific Mediator coordinates communications, facilitates scientist feedback, and ensures robustness through error reflection and recovery. By unifying planning, physics, and scientists, MAPPS enables flexible and reliable materials discovery with greater autonomy, achieving a five-fold improvement in stability, uniqueness, and novelty rates compared with prior generative models when evaluated on the MP-20 data. We provide extensive experiments across diverse tasks to show that MAPPS is a promising framework for autonomous materials discovery.
Complete and Efficient Graph Transformers for Crystal Material Property Prediction
Mar 18, 2024Abstract:Crystal structures are characterized by atomic bases within a primitive unit cell that repeats along a regular lattice throughout 3D space. The periodic and infinite nature of crystals poses unique challenges for geometric graph representation learning. Specifically, constructing graphs that effectively capture the complete geometric information of crystals and handle chiral crystals remains an unsolved and challenging problem. In this paper, we introduce a novel approach that utilizes the periodic patterns of unit cells to establish the lattice-based representation for each atom, enabling efficient and expressive graph representations of crystals. Furthermore, we propose ComFormer, a SE(3) transformer designed specifically for crystalline materials. ComFormer includes two variants; namely, iComFormer that employs invariant geometric descriptors of Euclidean distances and angles, and eComFormer that utilizes equivariant vector representations. Experimental results demonstrate the state-of-the-art predictive accuracy of ComFormer variants on various tasks across three widely-used crystal benchmarks. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).
Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems
Jul 17, 2023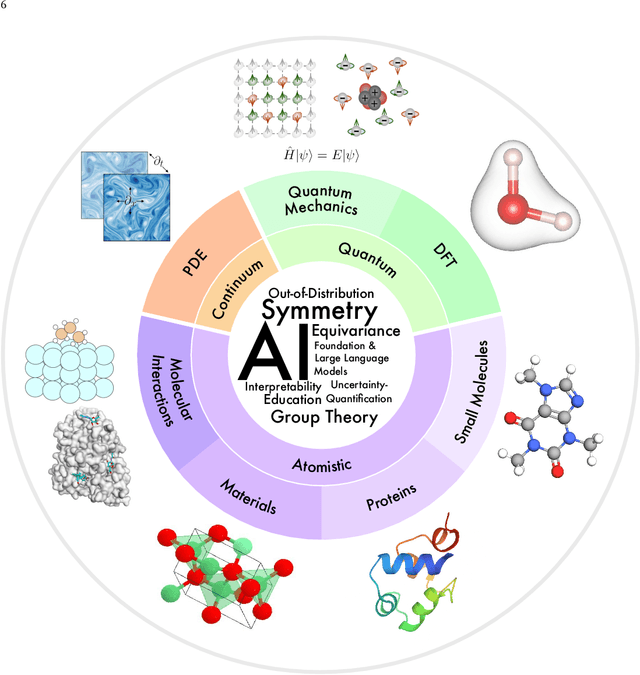
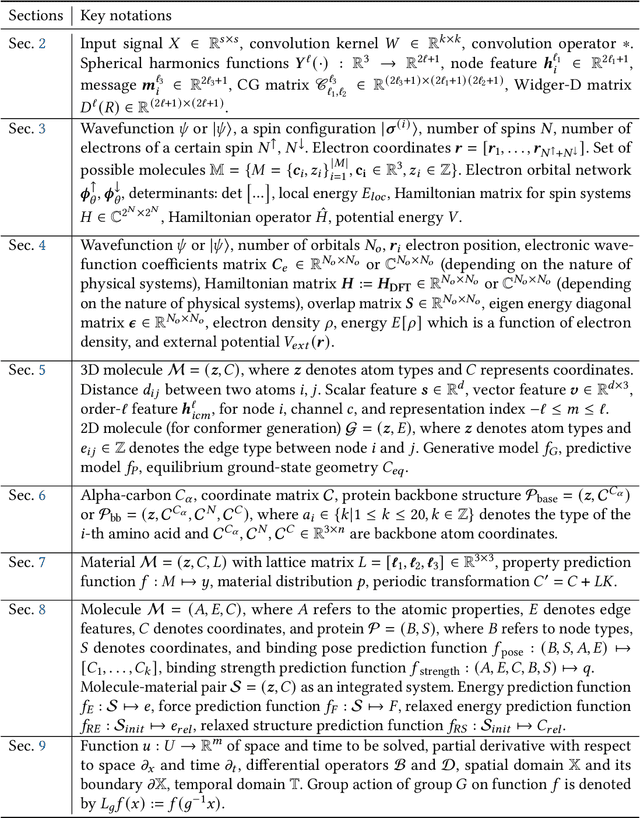
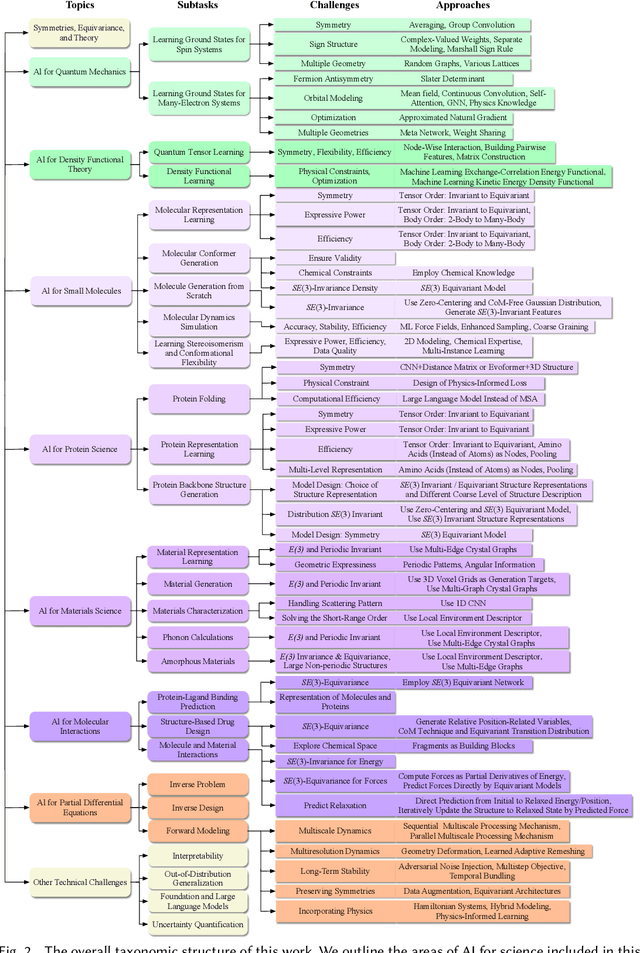

Abstract:Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.
QH9: A Quantum Hamiltonian Prediction Benchmark for QM9 Molecules
Jun 15, 2023



Abstract:Supervised machine learning approaches have been increasingly used in accelerating electronic structure prediction as surrogates of first-principle computational methods, such as density functional theory (DFT). While numerous quantum chemistry datasets focus on chemical properties and atomic forces, the ability to achieve accurate and efficient prediction of the Hamiltonian matrix is highly desired, as it is the most important and fundamental physical quantity that determines the quantum states of physical systems and chemical properties. In this work, we generate a new Quantum Hamiltonian dataset, named as QH9, to provide precise Hamiltonian matrices for 2,399 molecular dynamics trajectories and 130,831 stable molecular geometries, based on the QM9 dataset. By designing benchmark tasks with various molecules, we show that current machine learning models have the capacity to predict Hamiltonian matrices for arbitrary molecules. Both the QH9 dataset and the baseline models are provided to the community through an open-source benchmark, which can be highly valuable for developing machine learning methods and accelerating molecular and materials design for scientific and technological applications. Our benchmark is publicly available at https://github.com/divelab/AIRS/tree/main/OpenDFT/QHBench.
Efficient and Equivariant Graph Networks for Predicting Quantum Hamiltonian
Jun 08, 2023



Abstract:We consider the prediction of the Hamiltonian matrix, which finds use in quantum chemistry and condensed matter physics. Efficiency and equivariance are two important, but conflicting factors. In this work, we propose a SE(3)-equivariant network, named QHNet, that achieves efficiency and equivariance. Our key advance lies at the innovative design of QHNet architecture, which not only obeys the underlying symmetries, but also enables the reduction of number of tensor products by 92\%. In addition, QHNet prevents the exponential growth of channel dimension when more atom types are involved. We perform experiments on MD17 datasets, including four molecular systems. Experimental results show that our QHNet can achieve comparable performance to the state of the art methods at a significantly faster speed. Besides, our QHNet consumes 50\% less memory due to its streamlined architecture. Our code is publicly available as part of the AIRS library (\url{https://github.com/divelab/AIRS}).
Graph Neural Network for Hamiltonian-Based Material Property Prediction
May 27, 2020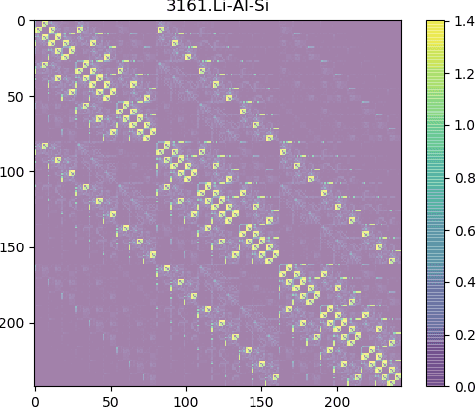


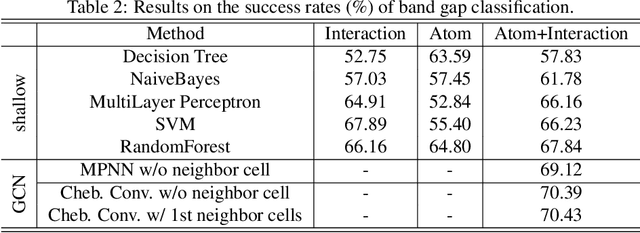
Abstract:Development of next-generation electronic devices for applications call for the discovery of quantum materials hosting novel electronic, magnetic, and topological properties. Traditional electronic structure methods require expensive computation time and memory consumption, thus a fast and accurate prediction model is desired with increasing importance. Representing the interactions among atomic orbitals in any material, a material Hamiltonian provides all the essential elements that control the structure-property correlations in inorganic compounds. Effective learning of material Hamiltonian by developing machine learning methodologies therefore offers a transformative approach to accelerate the discovery and design of quantum materials. With this motivation, we present and compare several different graph convolution networks that are able to predict the band gap for inorganic materials. The models are developed to incorporate two different features: the information of each orbital itself and the interaction between each other. The information of each orbital includes the name, relative coordinates with respect to the center of super cell and the atom number, while the interaction between orbitals are represented by the Hamiltonian matrix. The results show that our model can get a promising prediction accuracy with cross-validation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge