Learning Graph Quantized Tokenizers for Transformers

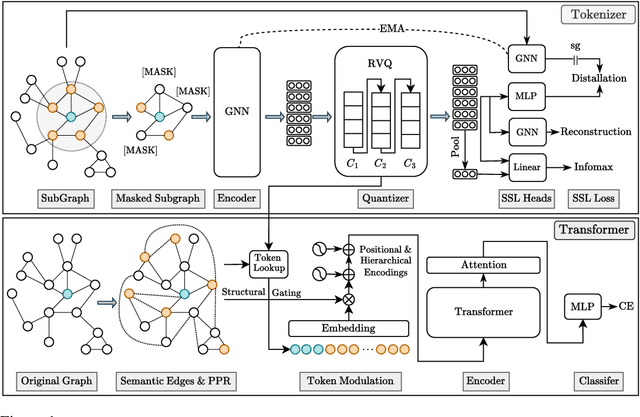
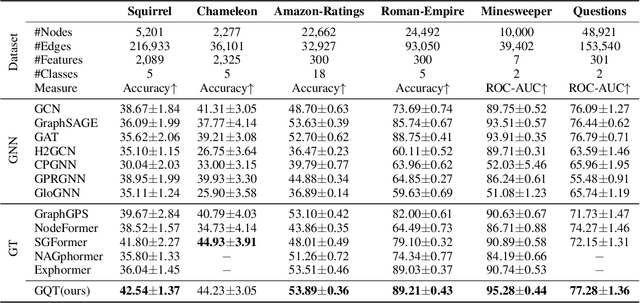
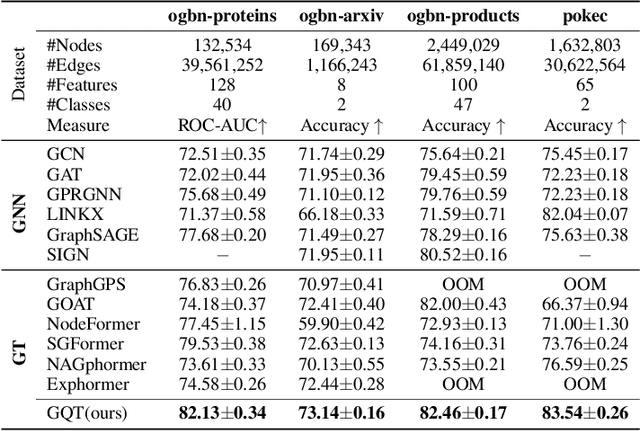
Transformers serve as the backbone architectures of Foundational Models, where a domain-specific tokenizer helps them adapt to various domains. Graph Transformers (GTs) have recently emerged as a leading model in geometric deep learning, outperforming Graph Neural Networks (GNNs) in various graph learning tasks. However, the development of tokenizers for graphs has lagged behind other modalities, with existing approaches relying on heuristics or GNNs co-trained with Transformers. To address this, we introduce GQT (\textbf{G}raph \textbf{Q}uantized \textbf{T}okenizer), which decouples tokenizer training from Transformer training by leveraging multi-task graph self-supervised learning, yielding robust and generalizable graph tokens. Furthermore, the GQT utilizes Residual Vector Quantization (RVQ) to learn hierarchical discrete tokens, resulting in significantly reduced memory requirements and improved generalization capabilities. By combining the GQT with token modulation, a Transformer encoder achieves state-of-the-art performance on 16 out of 18 benchmarks, including large-scale homophilic and heterophilic datasets. The code is available at: https://github.com/limei0307/graph-tokenizer

Language Models are Graph Learners

Language Models (LMs) are increasingly challenging the dominance of domain-specific models, including Graph Neural Networks (GNNs) and Graph Transformers (GTs), in graph learning tasks. Following this trend, we propose a novel approach that empowers off-the-shelf LMs to achieve performance comparable to state-of-the-art GNNs on node classification tasks, without requiring any architectural modification. By preserving the LM's original architecture, our approach retains a key benefit of LM instruction tuning: the ability to jointly train on diverse datasets, fostering greater flexibility and efficiency. To achieve this, we introduce two key augmentation strategies: (1) Enriching LMs' input using topological and semantic retrieval methods, which provide richer contextual information, and (2) guiding the LMs' classification process through a lightweight GNN classifier that effectively prunes class candidates. Our experiments on real-world datasets show that backbone Flan-T5 models equipped with these augmentation strategies outperform state-of-the-art text-output node classifiers and are comparable to top-performing vector-output node classifiers. By bridging the gap between specialized task-specific node classifiers and general LMs, this work paves the way for more versatile and widely applicable graph learning models. We will open-source the code upon publication.

Geometry Informed Tokenization of Molecules for Language Model Generation

We consider molecule generation in 3D space using language models (LMs), which requires discrete tokenization of 3D molecular geometries. Although tokenization of molecular graphs exists, that for 3D geometries is largely unexplored. Here, we attempt to bridge this gap by proposing the Geo2Seq, which converts molecular geometries into $SE(3)$-invariant 1D discrete sequences. Geo2Seq consists of canonical labeling and invariant spherical representation steps, which together maintain geometric and atomic fidelity in a format conducive to LMs. Our experiments show that, when coupled with Geo2Seq, various LMs excel in molecular geometry generation, especially in controlled generation tasks.

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

A Latent Diffusion Model for Protein Structure Generation

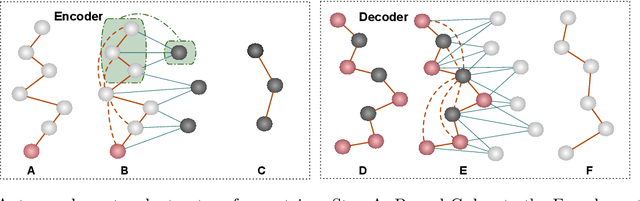
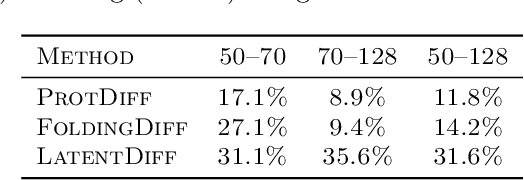
Proteins are complex biomolecules that perform a variety of crucial functions within living organisms. Designing and generating novel proteins can pave the way for many future synthetic biology applications, including drug discovery. However, it remains a challenging computational task due to the large modeling space of protein structures. In this study, we propose a latent diffusion model that can reduce the complexity of protein modeling while flexibly capturing the distribution of natural protein structures in a condensed latent space. Specifically, we propose an equivariant protein autoencoder that embeds proteins into a latent space and then uses an equivariant diffusion model to learn the distribution of the latent protein representations. Experimental results demonstrate that our method can effectively generate novel protein backbone structures with high designability and efficiency.

A new perspective on building efficient and expressive 3D equivariant graph neural networks

Geometric deep learning enables the encoding of physical symmetries in modeling 3D objects. Despite rapid progress in encoding 3D symmetries into Graph Neural Networks (GNNs), a comprehensive evaluation of the expressiveness of these networks through a local-to-global analysis lacks today. In this paper, we propose a local hierarchy of 3D isomorphism to evaluate the expressive power of equivariant GNNs and investigate the process of representing global geometric information from local patches. Our work leads to two crucial modules for designing expressive and efficient geometric GNNs; namely local substructure encoding (LSE) and frame transition encoding (FTE). To demonstrate the applicability of our theory, we propose LEFTNet which effectively implements these modules and achieves state-of-the-art performance on both scalar-valued and vector-valued molecular property prediction tasks. We further point out the design space for future developments of equivariant graph neural networks. Our codes are available at \url{https://github.com/yuanqidu/LeftNet}.

Learning Protein Representations via Complete 3D Graph Networks

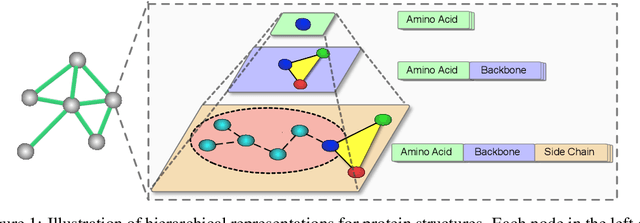
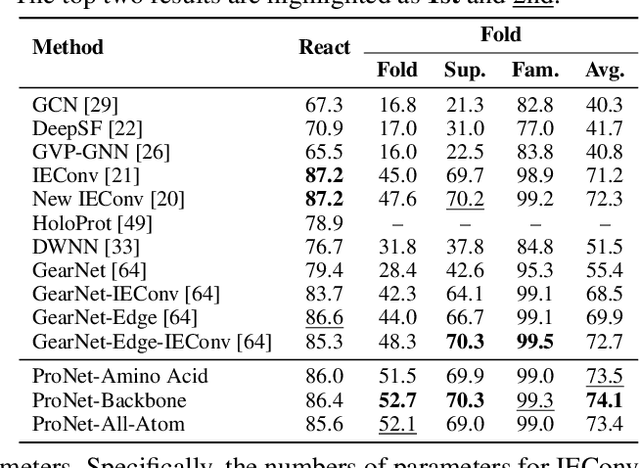
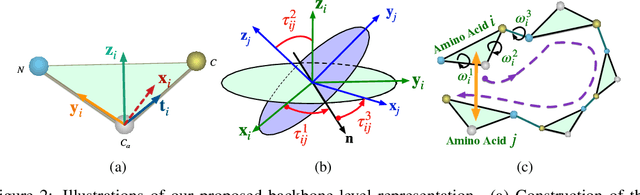
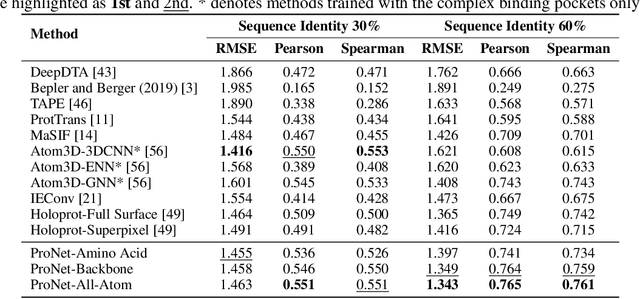
We consider representation learning for proteins with 3D structures. We build 3D graphs based on protein structures and develop graph networks to learn their representations. Depending on the levels of details that we wish to capture, protein representations can be computed at different levels, \emph{e.g.}, the amino acid, backbone, or all-atom levels. Importantly, there exist hierarchical relations among different levels. In this work, we propose to develop a novel hierarchical graph network, known as ProNet, to capture the relations. Our ProNet is very flexible and can be used to compute protein representations at different levels of granularity. We show that, given a base 3D graph network that is complete, our ProNet representations are also complete at all levels. To close the loop, we develop a complete and efficient 3D graph network to be used as a base model, making our ProNet complete. We conduct experiments on multiple downstream tasks. Results show that ProNet outperforms recent methods on most datasets. In addition, results indicate that different downstream tasks may require representations at different levels. Our code is available as part of the DIG library (\url{https://github.com/divelab/DIG}).

GraphFM: Improving Large-Scale GNN Training via Feature Momentum

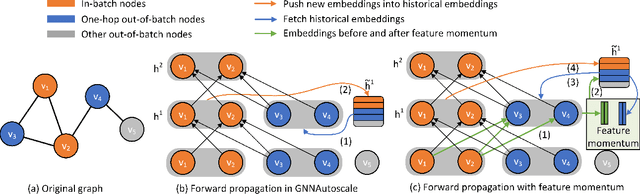
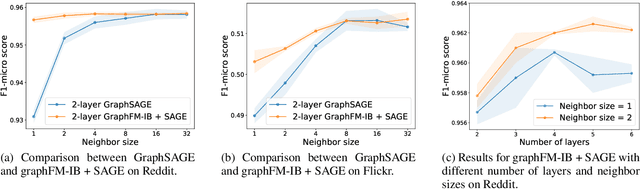
Training of graph neural networks (GNNs) for large-scale node classification is challenging. A key difficulty lies in obtaining accurate hidden node representations while avoiding the neighborhood explosion problem. Here, we propose a new technique, named feature momentum (FM), that uses a momentum step to incorporate historical embeddings when updating feature representations. We develop two specific algorithms, known as GraphFM-IB and GraphFM-OB, that consider in-batch and out-of-batch data, respectively. GraphFM-IB applies FM to in-batch sampled data, while GraphFM-OB applies FM to out-of-batch data that are 1-hop neighborhood of in-batch data. We provide a convergence analysis for GraphFM-IB and some theoretical insight for GraphFM-OB. Empirically, we observe that GraphFM-IB can effectively alleviate the neighborhood explosion problem of existing methods. In addition, GraphFM-OB achieves promising performance on multiple large-scale graph datasets.

ComENet: Towards Complete and Efficient Message Passing for 3D Molecular Graphs

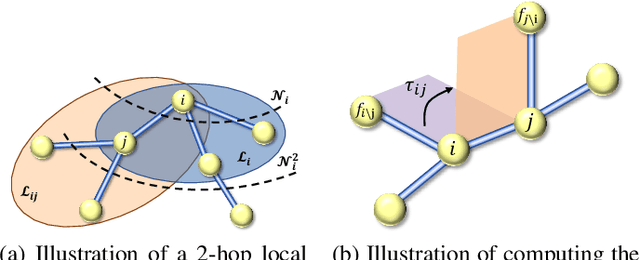
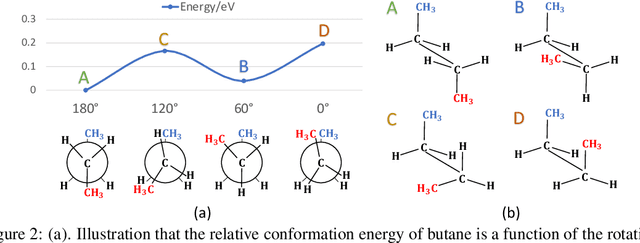
Many real-world data can be modeled as 3D graphs, but learning representations that incorporates 3D information completely and efficiently is challenging. Existing methods either use partial 3D information, or suffer from excessive computational cost. To incorporate 3D information completely and efficiently, we propose a novel message passing scheme that operates within 1-hop neighborhood. Our method guarantees full completeness of 3D information on 3D graphs by achieving global and local completeness. Notably, we propose the important rotation angles to fulfill global completeness. Additionally, we show that our method is orders of magnitude faster than prior methods. We provide rigorous proof of completeness and analysis of time complexity for our methods. As molecules are in essence quantum systems, we build the \underline{com}plete and \underline{e}fficient graph neural network (ComENet) by combing quantum inspired basis functions and the proposed message passing scheme. Experimental results demonstrate the capability and efficiency of ComENet, especially on real-world datasets that are large in both numbers and sizes of graphs. Our code is publicly available as part of the DIG library (\url{https://github.com/divelab/DIG}).

GOOD: A Graph Out-of-Distribution Benchmark

Out-of-distribution (OOD) learning deals with scenarios in which training and test data follow different distributions. Although general OOD problems have been intensively studied in machine learning, graph OOD is only an emerging area of research. Currently, there lacks a systematic benchmark tailored to graph OOD method evaluation. In this work, we aim at developing an OOD benchmark, known as GOOD, for graphs specifically. We explicitly make distinctions between covariate and concept shifts and design data splits that accurately reflect different shifts. We consider both graph and node prediction tasks as there are key differences when designing shifts. Overall, GOOD contains 8 datasets with 14 domain selections. When combined with covariate, concept, and no shifts, we obtain 42 different splits. We provide performance results on 7 commonly used baseline methods with 10 random runs. This results in 294 dataset-model combinations in total. Our results show significant performance gaps between in-distribution and OOD settings. Our results also shed light on different performance trends between covariate and concept shifts by different methods. Our GOOD benchmark is a growing project and expects to expand in both quantity and variety of resources as the area develops. The GOOD benchmark can be accessed via $\href{https://github.com/divelab/GOOD/}{\text{https://github.com/divelab/GOOD/}}$.