Learning Graph Quantized Tokenizers for Transformers

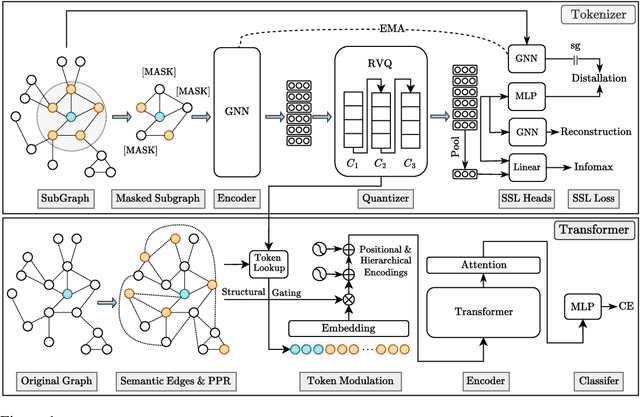
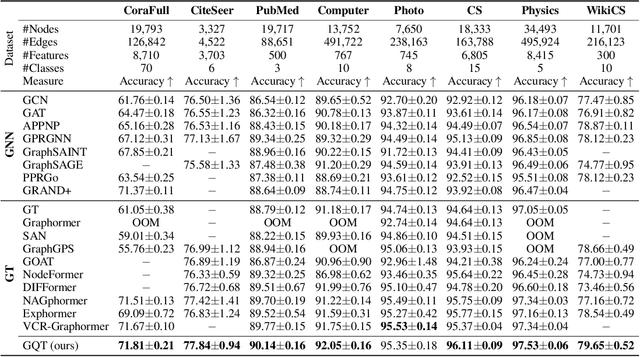
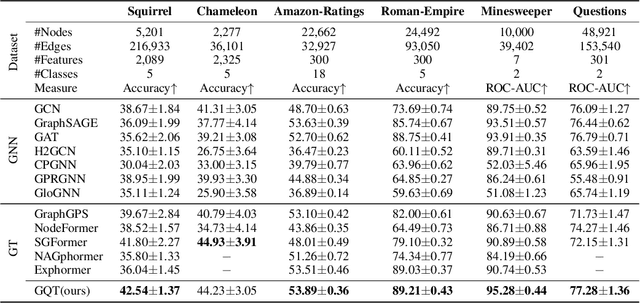
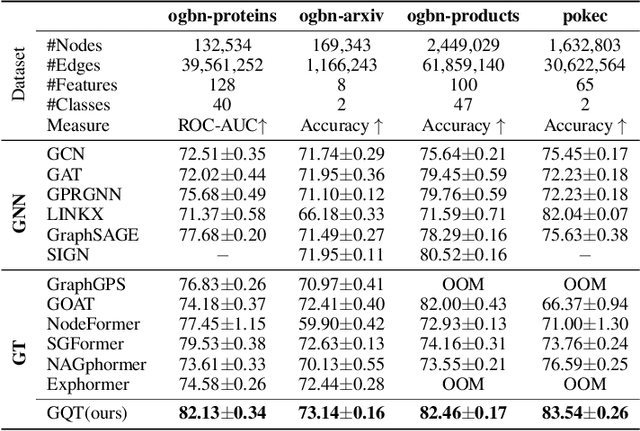
Transformers serve as the backbone architectures of Foundational Models, where a domain-specific tokenizer helps them adapt to various domains. Graph Transformers (GTs) have recently emerged as a leading model in geometric deep learning, outperforming Graph Neural Networks (GNNs) in various graph learning tasks. However, the development of tokenizers for graphs has lagged behind other modalities, with existing approaches relying on heuristics or GNNs co-trained with Transformers. To address this, we introduce GQT (\textbf{G}raph \textbf{Q}uantized \textbf{T}okenizer), which decouples tokenizer training from Transformer training by leveraging multi-task graph self-supervised learning, yielding robust and generalizable graph tokens. Furthermore, the GQT utilizes Residual Vector Quantization (RVQ) to learn hierarchical discrete tokens, resulting in significantly reduced memory requirements and improved generalization capabilities. By combining the GQT with token modulation, a Transformer encoder achieves state-of-the-art performance on 16 out of 18 benchmarks, including large-scale homophilic and heterophilic datasets. The code is available at: https://github.com/limei0307/graph-tokenizer

On the Generalization Capability of Temporal Graph Learning Algorithms: Theoretical Insights and a Simpler Method

Temporal Graph Learning (TGL) has become a prevalent technique across diverse real-world applications, especially in domains where data can be represented as a graph and evolves over time. Although TGL has recently seen notable progress in algorithmic solutions, its theoretical foundations remain largely unexplored. This paper aims at bridging this gap by investigating the generalization ability of different TGL algorithms (e.g., GNN-based, RNN-based, and memory-based methods) under the finite-wide over-parameterized regime. We establish the connection between the generalization error of TGL algorithms and "the number of layers/steps" in the GNN-/RNN-based TGL methods and "the feature-label alignment (FLA) score", where FLA can be used as a proxy for the expressive power and explains the performance of memory-based methods. Guided by our theoretical analysis, we propose Simplified-Temporal-Graph-Network, which enjoys a small generalization error, improved overall performance, and lower model complexity. Extensive experiments on real-world datasets demonstrate the effectiveness of our method. Our theoretical findings and proposed algorithm offer essential insights into TGL from a theoretical standpoint, laying the groundwork for the designing practical TGL algorithms in future studies.

BeMap: Balanced Message Passing for Fair Graph Neural Network

Graph Neural Network (GNN) has shown strong empirical performance in many downstream tasks by iteratively aggregating information from the local neighborhood of each node, i.e., message passing. However, concrete evidence has revealed that a graph neural network could be biased against certain demographic groups, which calls for the consideration of algorithmic fairness. Despite the increasing efforts in ensuring algorithmic fairness on graph neural networks, they often do not explicitly consider the induced bias caused by message passing in GNN during training. In this paper, we first investigate the problem of bias amplification in message passing. We empirically and theoretically demonstrate that message passing could amplify the bias when the 1-hop neighbors from different demographic groups are unbalanced. Guided by such analyses, we propose BeMap, a fair message passing method, that leverages a balance-aware sampling strategy to balance the number of the 1-hop neighbors of each node among different demographic groups. Extensive experiments on node classification demonstrate the efficacy of our proposed BeMap method in mitigating bias while maintaining classification accuracy.

Do We Really Need Complicated Model Architectures For Temporal Networks?

Recurrent neural network (RNN) and self-attention mechanism (SAM) are the de facto methods to extract spatial-temporal information for temporal graph learning. Interestingly, we found that although both RNN and SAM could lead to a good performance, in practice neither of them is always necessary. In this paper, we propose GraphMixer, a conceptually and technically simple architecture that consists of three components: (1) a link-encoder that is only based on multi-layer perceptrons (MLP) to summarize the information from temporal links, (2) a node-encoder that is only based on neighbor mean-pooling to summarize node information, and (3) an MLP-based link classifier that performs link prediction based on the outputs of the encoders. Despite its simplicity, GraphMixer attains an outstanding performance on temporal link prediction benchmarks with faster convergence and better generalization performance. These results motivate us to rethink the importance of simpler model architecture.

Efficiently Forgetting What You Have Learned in Graph Representation Learning via Projection

As privacy protection receives much attention, unlearning the effect of a specific node from a pre-trained graph learning model has become equally important. However, due to the node dependency in the graph-structured data, representation unlearning in Graph Neural Networks (GNNs) is challenging and less well explored. In this paper, we fill in this gap by first studying the unlearning problem in linear-GNNs, and then introducing its extension to non-linear structures. Given a set of nodes to unlearn, we propose PROJECTOR that unlearns by projecting the weight parameters of the pre-trained model onto a subspace that is irrelevant to features of the nodes to be forgotten. PROJECTOR could overcome the challenges caused by node dependency and enjoys a perfect data removal, i.e., the unlearned model parameters do not contain any information about the unlearned node features which is guaranteed by algorithmic construction. Empirical results on real-world datasets illustrate the effectiveness and efficiency of PROJECTOR.

Learn Locally, Correct Globally: A Distributed Algorithm for Training Graph Neural Networks

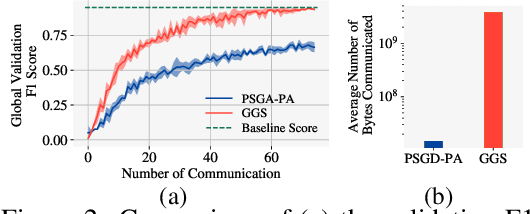
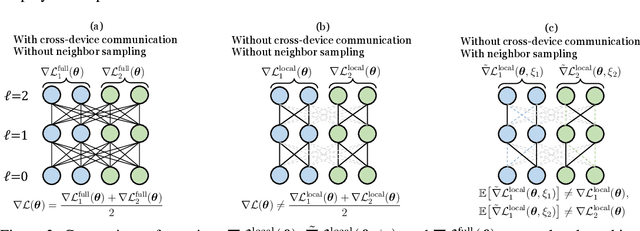
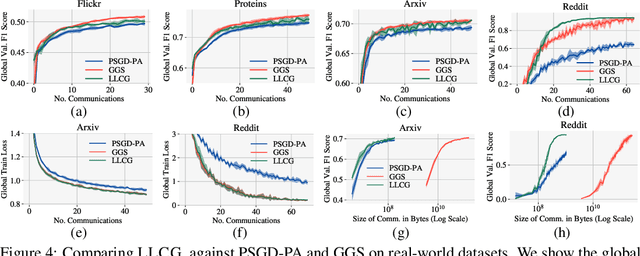
Despite the recent success of Graph Neural Networks (GNNs), training GNNs on large graphs remains challenging. The limited resource capacities of the existing servers, the dependency between nodes in a graph, and the privacy concern due to the centralized storage and model learning have spurred the need to design an effective distributed algorithm for GNN training. However, existing distributed GNN training methods impose either excessive communication costs or large memory overheads that hinders their scalability. To overcome these issues, we propose a communication-efficient distributed GNN training technique named $\text{{Learn Locally, Correct Globally}}$ (LLCG). To reduce the communication and memory overhead, each local machine in LLCG first trains a GNN on its local data by ignoring the dependency between nodes among different machines, then sends the locally trained model to the server for periodic model averaging. However, ignoring node dependency could result in significant performance degradation. To solve the performance degradation, we propose to apply $\text{{Global Server Corrections}}$ on the server to refine the locally learned models. We rigorously analyze the convergence of distributed methods with periodic model averaging for training GNNs and show that naively applying periodic model averaging but ignoring the dependency between nodes will suffer from an irreducible residual error. However, this residual error can be eliminated by utilizing the proposed global corrections to entail fast convergence rate. Extensive experiments on real-world datasets show that LLCG can significantly improve the efficiency without hurting the performance.

Dynamic Graph Representation Learning via Graph Transformer Networks

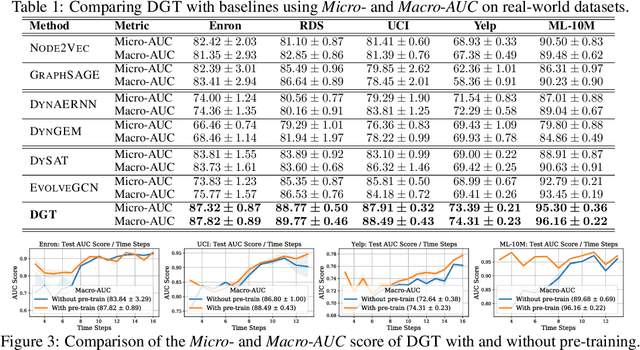
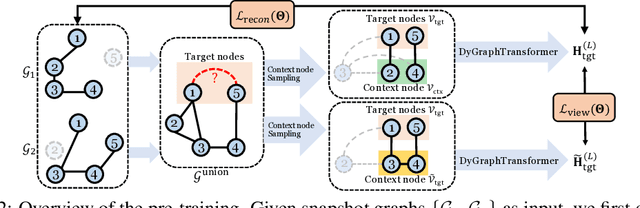
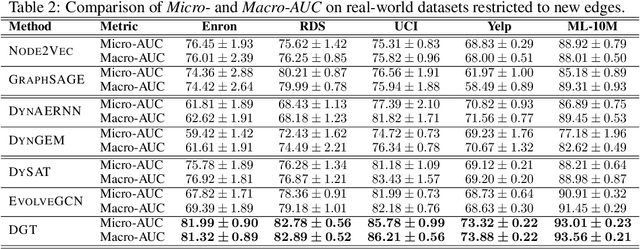
Dynamic graph representation learning is an important task with widespread applications. Previous methods on dynamic graph learning are usually sensitive to noisy graph information such as missing or spurious connections, which can yield degenerated performance and generalization. To overcome this challenge, we propose a Transformer-based dynamic graph learning method named Dynamic Graph Transformer (DGT) with spatial-temporal encoding to effectively learn graph topology and capture implicit links. To improve the generalization ability, we introduce two complementary self-supervised pre-training tasks and show that jointly optimizing the two pre-training tasks results in a smaller Bayesian error rate via an information-theoretic analysis. We also propose a temporal-union graph structure and a target-context node sampling strategy for efficient and scalable training. Extensive experiments on real-world datasets illustrate that DGT presents superior performance compared with several state-of-the-art baselines.

On Provable Benefits of Depth in Training Graph Convolutional Networks

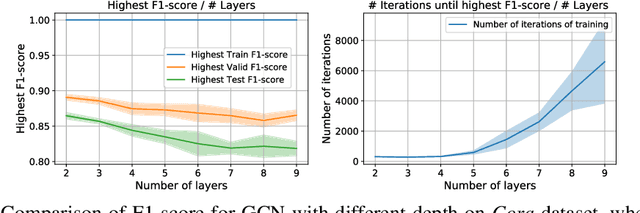
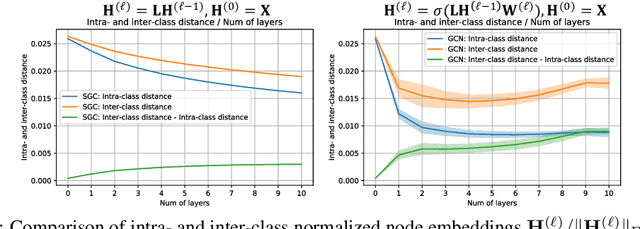
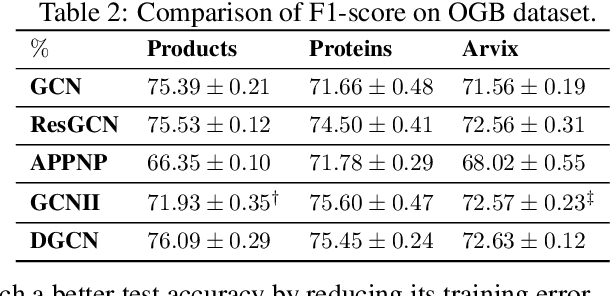
Graph Convolutional Networks (GCNs) are known to suffer from performance degradation as the number of layers increases, which is usually attributed to over-smoothing. Despite the apparent consensus, we observe that there exists a discrepancy between the theoretical understanding of over-smoothing and the practical capabilities of GCNs. Specifically, we argue that over-smoothing does not necessarily happen in practice, a deeper model is provably expressive, can converge to global optimum with linear convergence rate, and achieve very high training accuracy as long as properly trained. Despite being capable of achieving high training accuracy, empirical results show that the deeper models generalize poorly on the testing stage and existing theoretical understanding of such behavior remains elusive. To achieve better understanding, we carefully analyze the generalization capability of GCNs, and show that the training strategies to achieve high training accuracy significantly deteriorate the generalization capability of GCNs. Motivated by these findings, we propose a decoupled structure for GCNs that detaches weight matrices from feature propagation to preserve the expressive power and ensure good generalization performance. We conduct empirical evaluations on various synthetic and real-world datasets to validate the correctness of our theory.

On the Importance of Sampling in Learning Graph Convolutional Networks

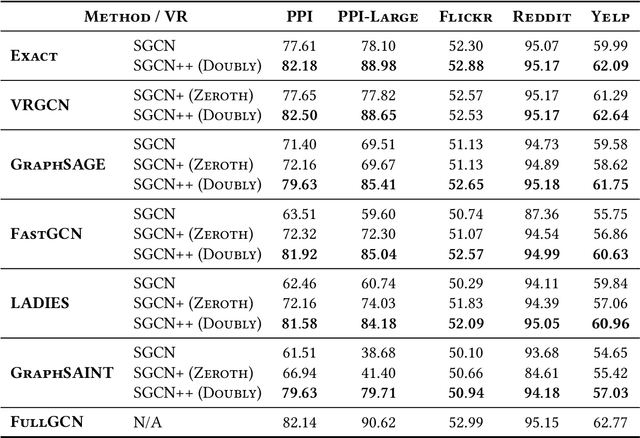
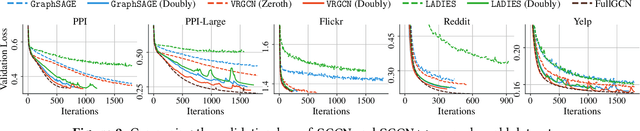
Graph Convolutional Networks (GCNs) have achieved impressive empirical advancement across a wide variety of graph-related applications. Despite their great success, training GCNs on large graphs suffers from computational and memory issues. A potential path to circumvent these obstacles is sampling-based methods, where at each layer a subset of nodes is sampled. Although recent studies have empirically demonstrated the effectiveness of sampling-based methods, these works lack theoretical convergence guarantees under realistic settings and cannot fully leverage the information of evolving parameters during optimization. In this paper, we describe and analyze a general \textbf{\textit{doubly variance reduction}} schema that can accelerate any sampling method under the memory budget. The motivating impetus for the proposed schema is a careful analysis for the variance of sampling methods where it is shown that the induced variance can be decomposed into node embedding approximation variance (\emph{zeroth-order variance}) during forward propagation and layerwise-gradient variance (\emph{first-order variance}) during backward propagation. We theoretically analyze the convergence of the proposed schema and show that it enjoys an $\mathcal{O}(1/T)$ convergence rate. We complement our theoretical results by integrating the proposed schema in different sampling methods and applying them to different large real-world graphs. Code is public available at~\url{https://github.com/CongWeilin/SGCN.git}.

Minimal Variance Sampling with Provable Guarantees for Fast Training of Graph Neural Networks

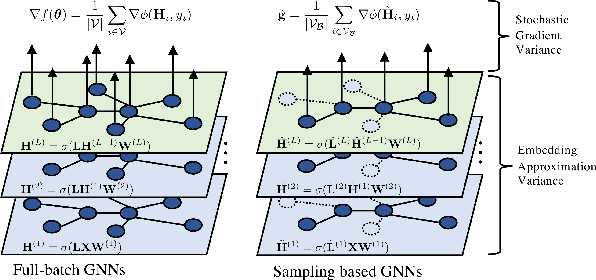
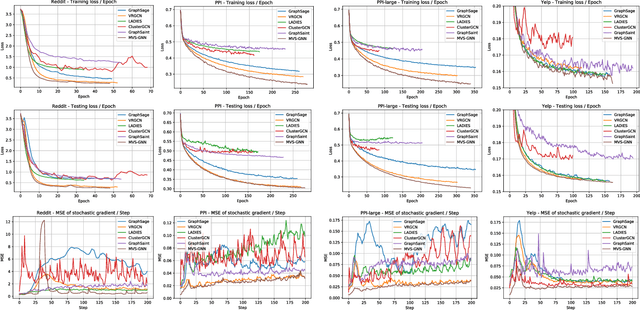
Sampling methods (e.g., node-wise, layer-wise, or subgraph) has become an indispensable strategy to speed up training large-scale Graph Neural Networks (GNNs). However, existing sampling methods are mostly based on the graph structural information and ignore the dynamicity of optimization, which leads to high variance in estimating the stochastic gradients. The high variance issue can be very pronounced in extremely large graphs, where it results in slow convergence and poor generalization. In this paper, we theoretically analyze the variance of sampling methods and show that, due to the composite structure of empirical risk, the variance of any sampling method can be decomposed into \textit{embedding approximation variance} in the forward stage and \textit{stochastic gradient variance} in the backward stage that necessities mitigating both types of variance to obtain faster convergence rate. We propose a decoupled variance reduction strategy that employs (approximate) gradient information to adaptively sample nodes with minimal variance, and explicitly reduces the variance introduced by embedding approximation. We show theoretically and empirically that the proposed method, even with smaller mini-batch sizes, enjoys a faster convergence rate and entails a better generalization compared to the existing methods.