Dynamic Graph Node Classification via Time Augmentation

Node classification for graph-structured data aims to classify nodes whose labels are unknown. While studies on static graphs are prevalent, few studies have focused on dynamic graph node classification. Node classification on dynamic graphs is challenging for two reasons. First, the model needs to capture both structural and temporal information, particularly on dynamic graphs with a long history and require large receptive fields. Second, model scalability becomes a significant concern as the size of the dynamic graph increases. To address these problems, we propose the Time Augmented Dynamic Graph Neural Network (TADGNN) framework. TADGNN consists of two modules: 1) a time augmentation module that captures the temporal evolution of nodes across time structurally, creating a time-augmented spatio-temporal graph, and 2) an information propagation module that learns the dynamic representations for each node across time using the constructed time-augmented graph. We perform node classification experiments on four dynamic graph benchmarks. Experimental results demonstrate that TADGNN framework outperforms several static and dynamic state-of-the-art (SOTA) GNN models while demonstrating superior scalability. We also conduct theoretical and empirical analyses to validate the efficiency of the proposed method. Our code is available at https://sites.google.com/view/tadgnn.

Embedding Compression with Hashing for Efficient Representation Learning in Large-Scale Graph

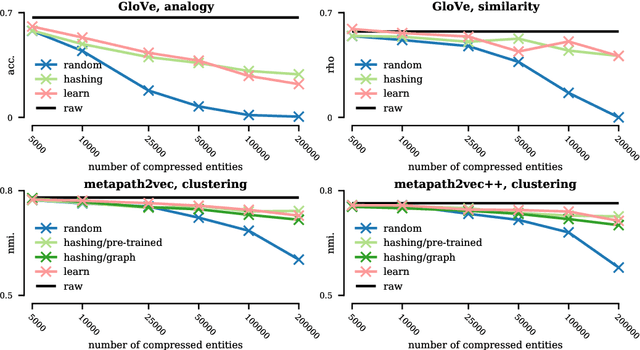
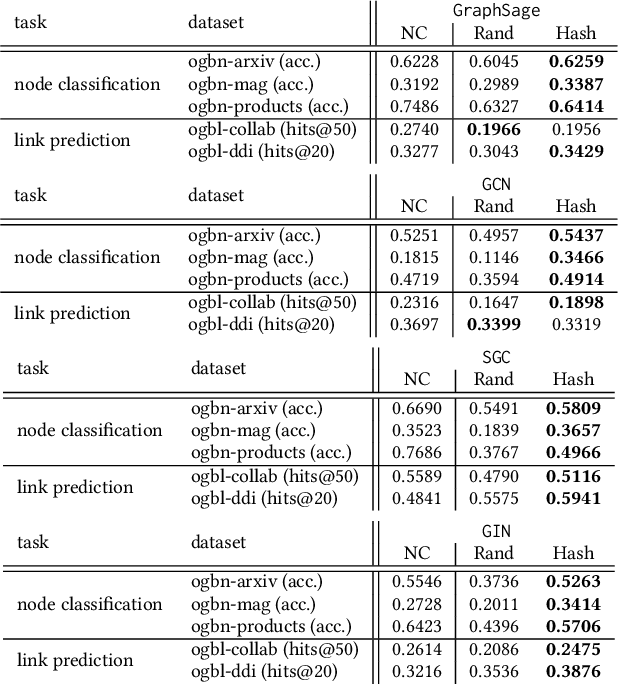
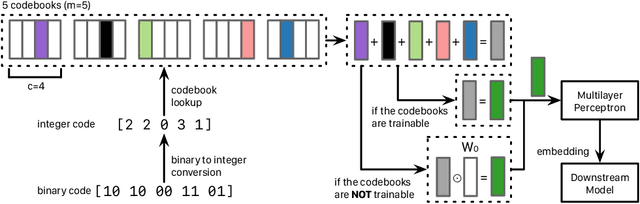
Graph neural networks (GNNs) are deep learning models designed specifically for graph data, and they typically rely on node features as the input to the first layer. When applying such a type of network on the graph without node features, one can extract simple graph-based node features (e.g., number of degrees) or learn the input node representations (i.e., embeddings) when training the network. While the latter approach, which trains node embeddings, more likely leads to better performance, the number of parameters associated with the embeddings grows linearly with the number of nodes. It is therefore impractical to train the input node embeddings together with GNNs within graphics processing unit (GPU) memory in an end-to-end fashion when dealing with industrial-scale graph data. Inspired by the embedding compression methods developed for natural language processing (NLP) tasks, we develop a node embedding compression method where each node is compactly represented with a bit vector instead of a floating-point vector. The parameters utilized in the compression method can be trained together with GNNs. We show that the proposed node embedding compression method achieves superior performance compared to the alternatives.

Dynamic Graph Representation Learning via Graph Transformer Networks

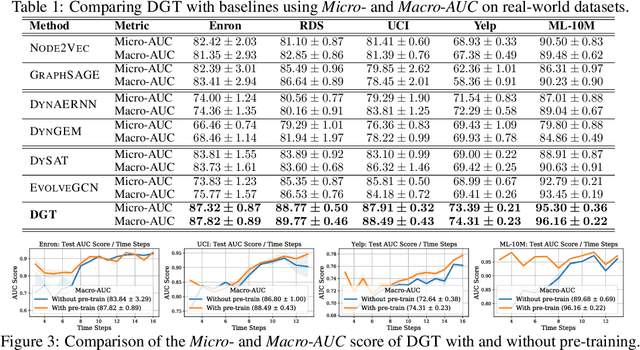
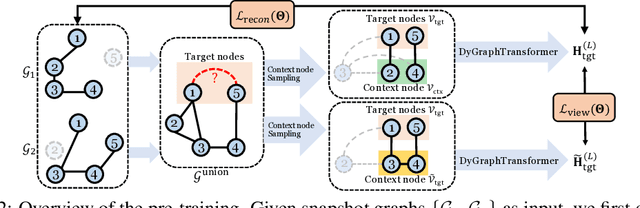
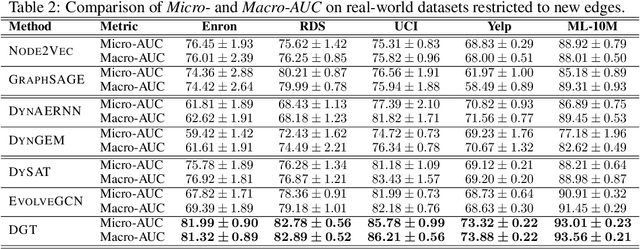
Dynamic graph representation learning is an important task with widespread applications. Previous methods on dynamic graph learning are usually sensitive to noisy graph information such as missing or spurious connections, which can yield degenerated performance and generalization. To overcome this challenge, we propose a Transformer-based dynamic graph learning method named Dynamic Graph Transformer (DGT) with spatial-temporal encoding to effectively learn graph topology and capture implicit links. To improve the generalization ability, we introduce two complementary self-supervised pre-training tasks and show that jointly optimizing the two pre-training tasks results in a smaller Bayesian error rate via an information-theoretic analysis. We also propose a temporal-union graph structure and a target-context node sampling strategy for efficient and scalable training. Extensive experiments on real-world datasets illustrate that DGT presents superior performance compared with several state-of-the-art baselines.

Event2Graph: Event-driven Bipartite Graph for Multivariate Time-series Anomaly Detection

Modeling inter-dependencies between time-series is the key to achieve high performance in anomaly detection for multivariate time-series data. The de-facto solution to model the dependencies is to feed the data into a recurrent neural network (RNN). However, the fully connected network structure underneath the RNN (either GRU or LSTM) assumes a static and complete dependency graph between time-series, which may not hold in many real-world applications. To alleviate this assumption, we propose a dynamic bipartite graph structure to encode the inter-dependencies between time-series. More concretely, we model time series as one type of nodes, and the time series segments (regarded as event) as another type of nodes, where the edge between two types of nodes describe a temporal pattern occurred on a specific time series at a certain time. Based on this design, relations between time series can be explicitly modelled via dynamic connections to event nodes, and the multivariate time-series anomaly detection problem can be formulated as a self-supervised, edge stream prediction problem in dynamic graphs. We conducted extensive experiments to demonstrate the effectiveness of the design.