BaKlaVa -- Budgeted Allocation of KV cache for Long-context Inference

In Large Language Model (LLM) inference, Key-Value (KV) caches (KV-caches) are essential for reducing time complexity. However, they result in a linear increase in GPU memory as the context length grows. While recent work explores KV-cache eviction and compression policies to reduce memory usage, they often consider uniform KV-caches across all attention heads, leading to suboptimal performance. We introduce BaKlaVa, a method to allocate optimal memory for individual KV-caches across the model by estimating the importance of each KV-cache. Our empirical analysis demonstrates that not all KV-caches are equally critical for LLM performance. Using a one-time profiling approach, BaKlaVa assigns optimal memory budgets to each KV-cache. We evaluated our method on LLaMA-3-8B, and Qwen2.5-7B models, achieving up to a 70\% compression ratio while keeping baseline performance and delivering up to an order-of-magnitude accuracy improvement at higher compression levels.

Minimal Variance Sampling with Provable Guarantees for Fast Training of Graph Neural Networks

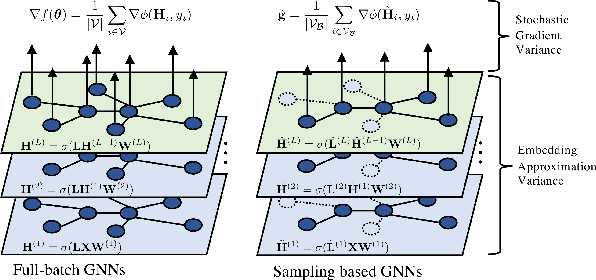
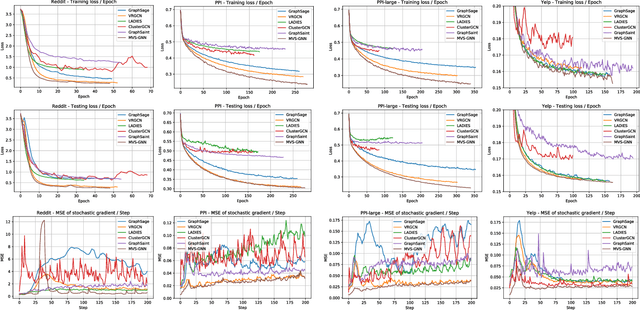
Sampling methods (e.g., node-wise, layer-wise, or subgraph) has become an indispensable strategy to speed up training large-scale Graph Neural Networks (GNNs). However, existing sampling methods are mostly based on the graph structural information and ignore the dynamicity of optimization, which leads to high variance in estimating the stochastic gradients. The high variance issue can be very pronounced in extremely large graphs, where it results in slow convergence and poor generalization. In this paper, we theoretically analyze the variance of sampling methods and show that, due to the composite structure of empirical risk, the variance of any sampling method can be decomposed into \textit{embedding approximation variance} in the forward stage and \textit{stochastic gradient variance} in the backward stage that necessities mitigating both types of variance to obtain faster convergence rate. We propose a decoupled variance reduction strategy that employs (approximate) gradient information to adaptively sample nodes with minimal variance, and explicitly reduces the variance introduced by embedding approximation. We show theoretically and empirically that the proposed method, even with smaller mini-batch sizes, enjoys a faster convergence rate and entails a better generalization compared to the existing methods.