On Provable Benefits of Depth in Training Graph Convolutional Networks
Paper and Code
Oct 28, 2021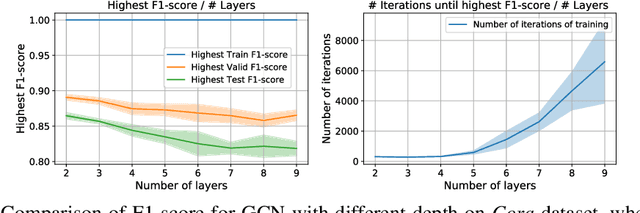

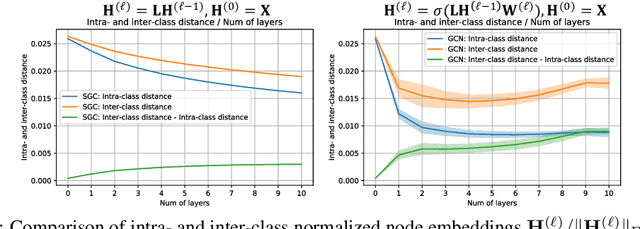
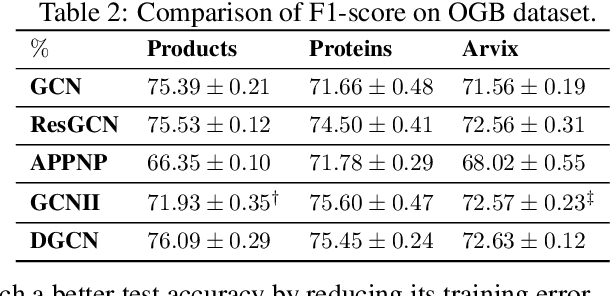
Graph Convolutional Networks (GCNs) are known to suffer from performance degradation as the number of layers increases, which is usually attributed to over-smoothing. Despite the apparent consensus, we observe that there exists a discrepancy between the theoretical understanding of over-smoothing and the practical capabilities of GCNs. Specifically, we argue that over-smoothing does not necessarily happen in practice, a deeper model is provably expressive, can converge to global optimum with linear convergence rate, and achieve very high training accuracy as long as properly trained. Despite being capable of achieving high training accuracy, empirical results show that the deeper models generalize poorly on the testing stage and existing theoretical understanding of such behavior remains elusive. To achieve better understanding, we carefully analyze the generalization capability of GCNs, and show that the training strategies to achieve high training accuracy significantly deteriorate the generalization capability of GCNs. Motivated by these findings, we propose a decoupled structure for GCNs that detaches weight matrices from feature propagation to preserve the expressive power and ensure good generalization performance. We conduct empirical evaluations on various synthetic and real-world datasets to validate the correctness of our theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge