Learning Graph Quantized Tokenizers for Transformers

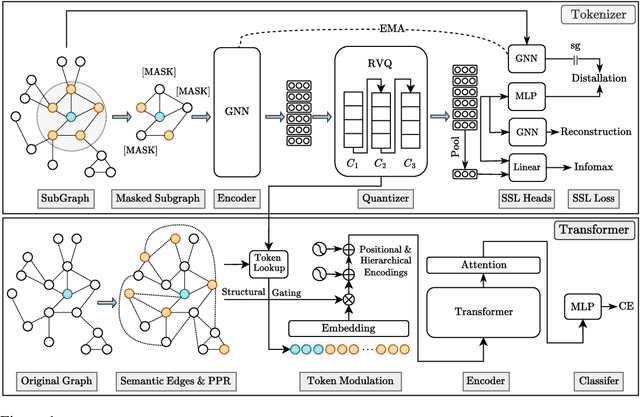
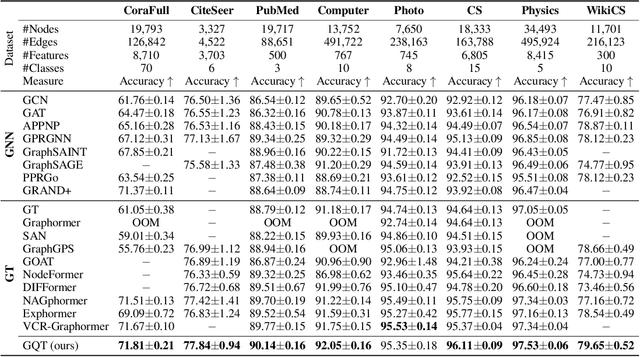
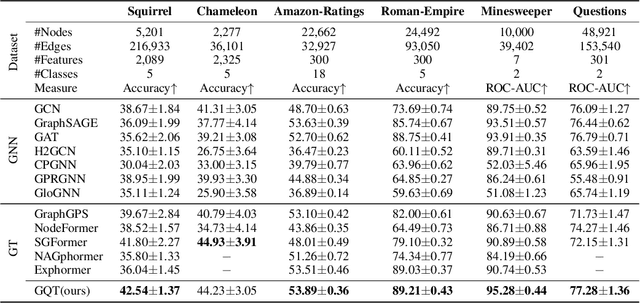
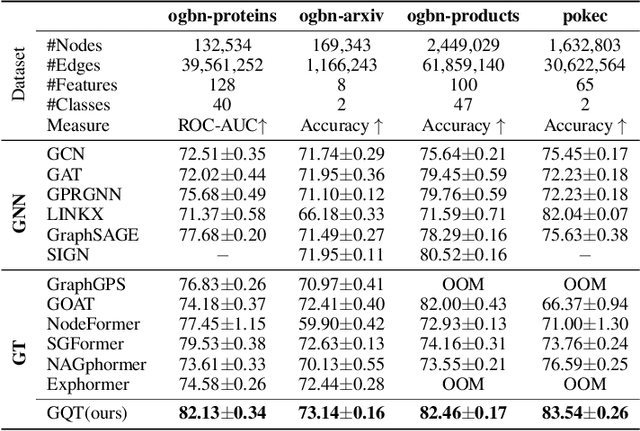
Transformers serve as the backbone architectures of Foundational Models, where a domain-specific tokenizer helps them adapt to various domains. Graph Transformers (GTs) have recently emerged as a leading model in geometric deep learning, outperforming Graph Neural Networks (GNNs) in various graph learning tasks. However, the development of tokenizers for graphs has lagged behind other modalities, with existing approaches relying on heuristics or GNNs co-trained with Transformers. To address this, we introduce GQT (\textbf{G}raph \textbf{Q}uantized \textbf{T}okenizer), which decouples tokenizer training from Transformer training by leveraging multi-task graph self-supervised learning, yielding robust and generalizable graph tokens. Furthermore, the GQT utilizes Residual Vector Quantization (RVQ) to learn hierarchical discrete tokens, resulting in significantly reduced memory requirements and improved generalization capabilities. By combining the GQT with token modulation, a Transformer encoder achieves state-of-the-art performance on 16 out of 18 benchmarks, including large-scale homophilic and heterophilic datasets. The code is available at: https://github.com/limei0307/graph-tokenizer

Do We Really Need Complicated Model Architectures For Temporal Networks?

Recurrent neural network (RNN) and self-attention mechanism (SAM) are the de facto methods to extract spatial-temporal information for temporal graph learning. Interestingly, we found that although both RNN and SAM could lead to a good performance, in practice neither of them is always necessary. In this paper, we propose GraphMixer, a conceptually and technically simple architecture that consists of three components: (1) a link-encoder that is only based on multi-layer perceptrons (MLP) to summarize the information from temporal links, (2) a node-encoder that is only based on neighbor mean-pooling to summarize node information, and (3) an MLP-based link classifier that performs link prediction based on the outputs of the encoders. Despite its simplicity, GraphMixer attains an outstanding performance on temporal link prediction benchmarks with faster convergence and better generalization performance. These results motivate us to rethink the importance of simpler model architecture.

Frequency-aware SGD for Efficient Embedding Learning with Provable Benefits

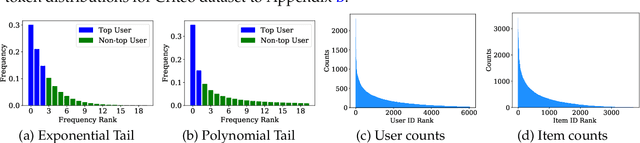
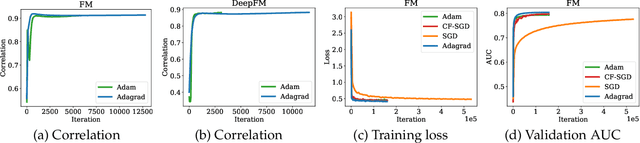
Embedding learning has found widespread applications in recommendation systems and natural language modeling, among other domains. To learn quality embeddings efficiently, adaptive learning rate algorithms have demonstrated superior empirical performance over SGD, largely accredited to their token-dependent learning rate. However, the underlying mechanism for the efficiency of token-dependent learning rate remains underexplored. We show that incorporating frequency information of tokens in the embedding learning problems leads to provably efficient algorithms, and demonstrate that common adaptive algorithms implicitly exploit the frequency information to a large extent. Specifically, we propose (Counter-based) Frequency-aware Stochastic Gradient Descent, which applies a frequency-dependent learning rate for each token, and exhibits provable speed-up compared to SGD when the token distribution is imbalanced. Empirically, we show the proposed algorithms are able to improve or match adaptive algorithms on benchmark recommendation tasks and a large-scale industrial recommendation system, closing the performance gap between SGD and adaptive algorithms. Our results are the first to show token-dependent learning rate provably improves convergence for non-convex embedding learning problems.

Multivariate Spatiotemporal Hawkes Processes and Network Reconstruction

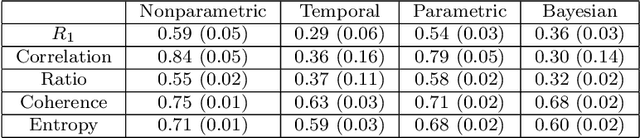
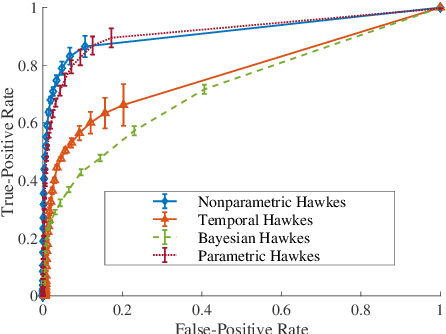
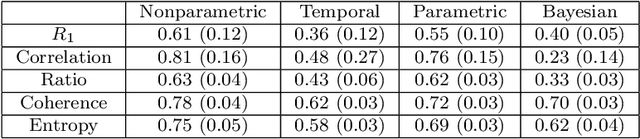
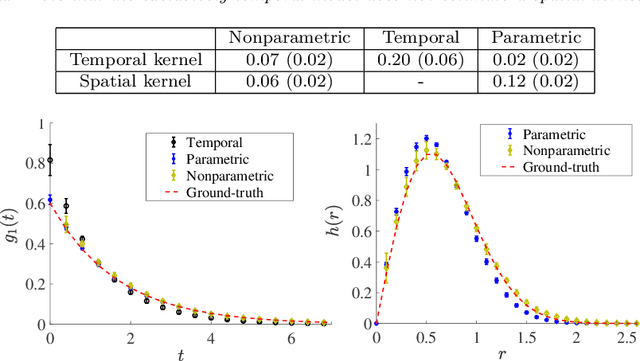
There is often latent network structure in spatial and temporal data and the tools of network analysis can yield fascinating insights into such data. In this paper, we develop a nonparametric method for network reconstruction from spatiotemporal data sets using multivariate Hawkes processes. In contrast to prior work on network reconstruction with point-process models, which has often focused on exclusively temporal information, our approach uses both temporal and spatial information and does not assume a specific parametric form of network dynamics. This leads to an effective way of recovering an underlying network. We illustrate our approach using both synthetic networks and networks constructed from real-world data sets (a location-based social media network, a narrative of crime events, and violent gang crimes). Our results demonstrate that, in comparison to using only temporal data, our spatiotemporal approach yields improved network reconstruction, providing a basis for meaningful subsequent analysis --- such as community structure and motif analysis --- of the reconstructed networks.

Graph-Based Deep Modeling and Real Time Forecasting of Sparse Spatio-Temporal Data

We present a generic framework for spatio-temporal (ST) data modeling, analysis, and forecasting, with a special focus on data that is sparse in both space and time. Our multi-scaled framework is a seamless coupling of two major components: a self-exciting point process that models the macroscale statistical behaviors of the ST data and a graph structured recurrent neural network (GSRNN) to discover the microscale patterns of the ST data on the inferred graph. This novel deep neural network (DNN) incorporates the real time interactions of the graph nodes to enable more accurate real time forecasting. The effectiveness of our method is demonstrated on both crime and traffic forecasting.