Learning to Control the Smoothness of Graph Convolutional Network Features

The pioneering work of Oono and Suzuki [ICLR, 2020] and Cai and Wang [arXiv:2006.13318] initializes the analysis of the smoothness of graph convolutional network (GCN) features. Their results reveal an intricate empirical correlation between node classification accuracy and the ratio of smooth to non-smooth feature components. However, the optimal ratio that favors node classification is unknown, and the non-smooth features of deep GCN with ReLU or leaky ReLU activation function diminish. In this paper, we propose a new strategy to let GCN learn node features with a desired smoothness -- adapting to data and tasks -- to enhance node classification. Our approach has three key steps: (1) We establish a geometric relationship between the input and output of ReLU or leaky ReLU. (2) Building on our geometric insights, we augment the message-passing process of graph convolutional layers (GCLs) with a learnable term to modulate the smoothness of node features with computational efficiency. (3) We investigate the achievable ratio between smooth and non-smooth feature components for GCNs with the augmented message-passing scheme. Our extensive numerical results show that the augmented message-passing schemes significantly improve node classification for GCN and some related models.

Deep Learning with Data Privacy via Residual Perturbation

Protecting data privacy in deep learning (DL) is of crucial importance. Several celebrated privacy notions have been established and used for privacy-preserving DL. However, many existing mechanisms achieve privacy at the cost of significant utility degradation and computational overhead. In this paper, we propose a stochastic differential equation-based residual perturbation for privacy-preserving DL, which injects Gaussian noise into each residual mapping of ResNets. Theoretically, we prove that residual perturbation guarantees differential privacy (DP) and reduces the generalization gap of DL. Empirically, we show that residual perturbation is computationally efficient and outperforms the state-of-the-art differentially private stochastic gradient descent (DPSGD) in utility maintenance without sacrificing membership privacy.

Adaptive and Implicit Regularization for Matrix Completion

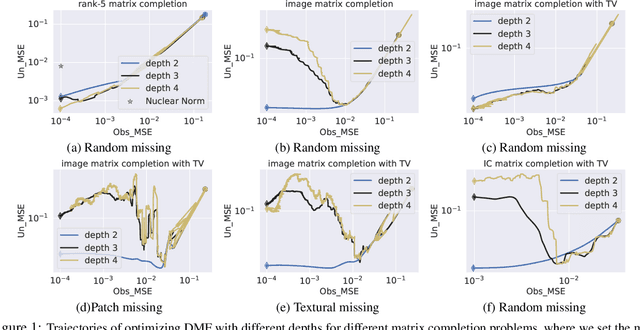
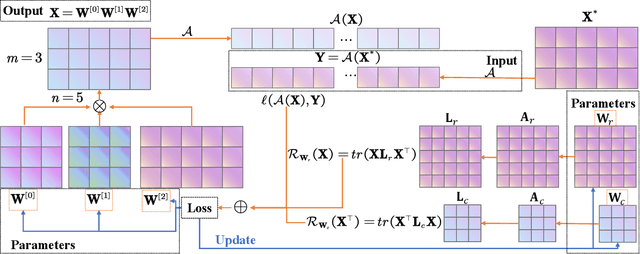
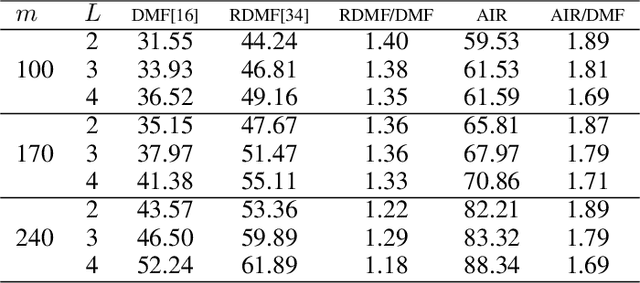
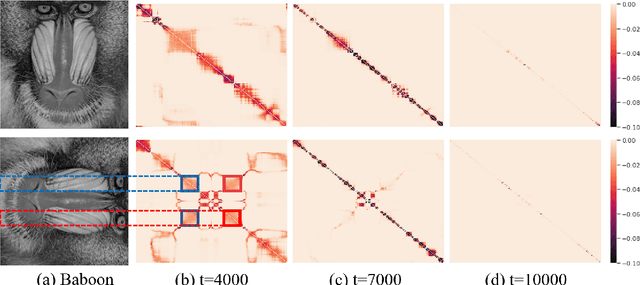
The explicit low-rank regularization, e.g., nuclear norm regularization, has been widely used in imaging sciences. However, it has been found that implicit regularization outperforms explicit ones in various image processing tasks. Another issue is that the fixed explicit regularization limits the applicability to broad images since different images favor different features captured by different explicit regularizations. As such, this paper proposes a new adaptive and implicit low-rank regularization that captures the low-rank prior dynamically from the training data. The core of our new adaptive and implicit low-rank regularization is parameterizing the Laplacian matrix in the Dirichlet energy-based regularization, which we call the regularization AIR. Theoretically, we show that the adaptive regularization of \ReTwo{AIR} enhances the implicit regularization and vanishes at the end of training. We validate AIR's effectiveness on various benchmark tasks, indicating that the AIR is particularly favorable for the scenarios when the missing entries are non-uniform. The code can be found at https://github.com/lizhemin15/AIR-Net.

Momentum Transformer: Closing the Performance Gap Between Self-attention and Its Linearization

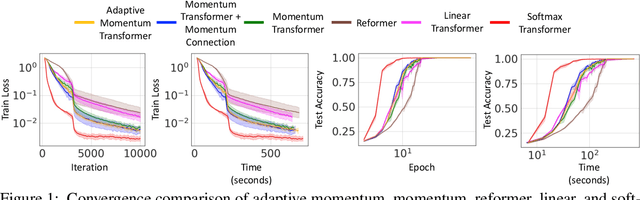
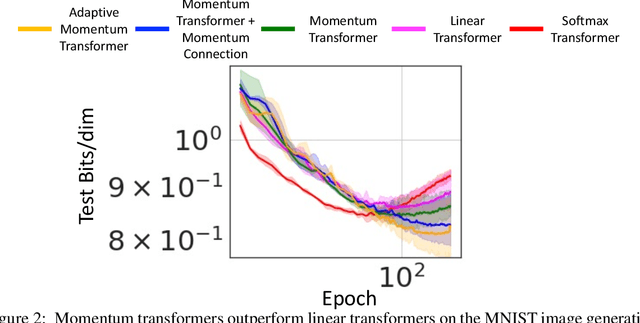
Transformers have achieved remarkable success in sequence modeling and beyond but suffer from quadratic computational and memory complexities with respect to the length of the input sequence. Leveraging techniques include sparse and linear attention and hashing tricks; efficient transformers have been proposed to reduce the quadratic complexity of transformers but significantly degrade the accuracy. In response, we first interpret the linear attention and residual connections in computing the attention map as gradient descent steps. We then introduce momentum into these components and propose the \emph{momentum transformer}, which utilizes momentum to improve the accuracy of linear transformers while maintaining linear memory and computational complexities. Furthermore, we develop an adaptive strategy to compute the momentum value for our model based on the optimal momentum for quadratic optimization. This adaptive momentum eliminates the need to search for the optimal momentum value and further enhances the performance of the momentum transformer. A range of experiments on both autoregressive and non-autoregressive tasks, including image generation and machine translation, demonstrate that the momentum transformer outperforms popular linear transformers in training efficiency and accuracy.

Proximal Implicit ODE Solvers for Accelerating Learning Neural ODEs

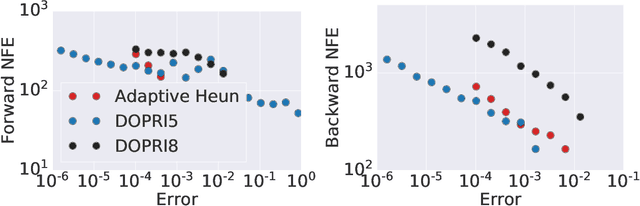
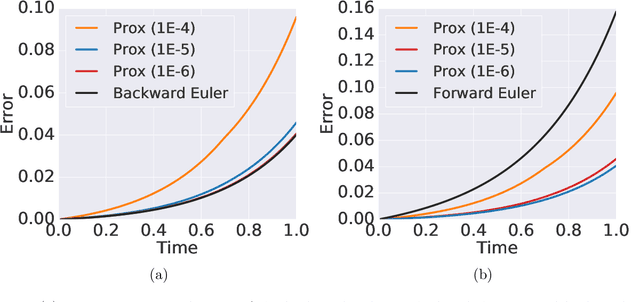
Learning neural ODEs often requires solving very stiff ODE systems, primarily using explicit adaptive step size ODE solvers. These solvers are computationally expensive, requiring the use of tiny step sizes for numerical stability and accuracy guarantees. This paper considers learning neural ODEs using implicit ODE solvers of different orders leveraging proximal operators. The proximal implicit solver consists of inner-outer iterations: the inner iterations approximate each implicit update step using a fast optimization algorithm, and the outer iterations solve the ODE system over time. The proximal implicit ODE solver guarantees superiority over explicit solvers in numerical stability and computational efficiency. We validate the advantages of proximal implicit solvers over existing popular neural ODE solvers on various challenging benchmark tasks, including learning continuous-depth graph neural networks and continuous normalizing flows.

Learning POD of Complex Dynamics Using Heavy-ball Neural ODEs

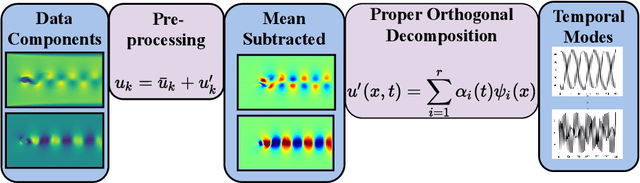
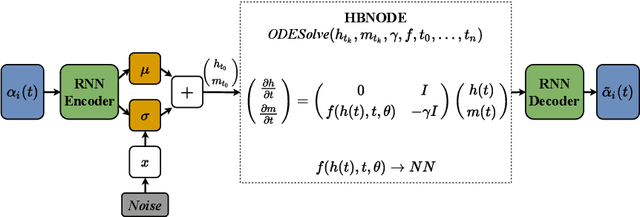
Proper orthogonal decomposition (POD) allows reduced-order modeling of complex dynamical systems at a substantial level, while maintaining a high degree of accuracy in modeling the underlying dynamical systems. Advances in machine learning algorithms enable learning POD-based dynamics from data and making accurate and fast predictions of dynamical systems. In this paper, we leverage the recently proposed heavy-ball neural ODEs (HBNODEs) [Xia et al. NeurIPS, 2021] for learning data-driven reduced-order models (ROMs) in the POD context, in particular, for learning dynamics of time-varying coefficients generated by the POD analysis on training snapshots generated from solving full order models. HBNODE enjoys several practical advantages for learning POD-based ROMs with theoretical guarantees, including 1) HBNODE can learn long-term dependencies effectively from sequential observations and 2) HBNODE is computationally efficient in both training and testing. We compare HBNODE with other popular ROMs on several complex dynamical systems, including the von K\'{a}rm\'{a}n Street flow, the Kurganov-Petrova-Popov equation, and the one-dimensional Euler equations for fluids modeling.

glassoformer: a query-sparse transformer for post-fault power grid voltage prediction

We propose GLassoformer, a novel and efficient transformer architecture leveraging group Lasso regularization to reduce the number of queries of the standard self-attention mechanism. Due to the sparsified queries, GLassoformer is more computationally efficient than the standard transformers. On the power grid post-fault voltage prediction task, GLassoformer shows remarkably better prediction than many existing benchmark algorithms in terms of accuracy and stability.

Efficient and Reliable Overlay Networks for Decentralized Federated Learning

We propose near-optimal overlay networks based on $d$-regular expander graphs to accelerate decentralized federated learning (DFL) and improve its generalization. In DFL a massive number of clients are connected by an overlay network, and they solve machine learning problems collaboratively without sharing raw data. Our overlay network design integrates spectral graph theory and the theoretical convergence and generalization bounds for DFL. As such, our proposed overlay networks accelerate convergence, improve generalization, and enhance robustness to clients failures in DFL with theoretical guarantees. Also, we present an efficient algorithm to convert a given graph to a practical overlay network and maintaining the network topology after potential client failures. We numerically verify the advantages of DFL with our proposed networks on various benchmark tasks, ranging from image classification to language modeling using hundreds of clients.

How Does Momentum Benefit Deep Neural Networks Architecture Design? A Few Case Studies

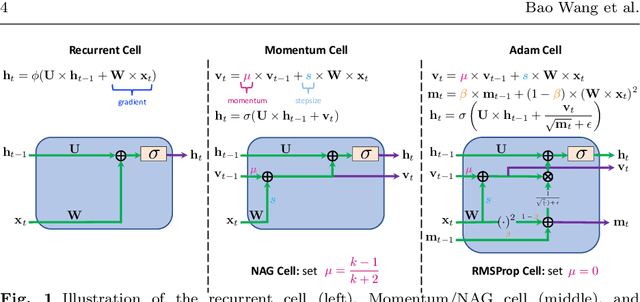
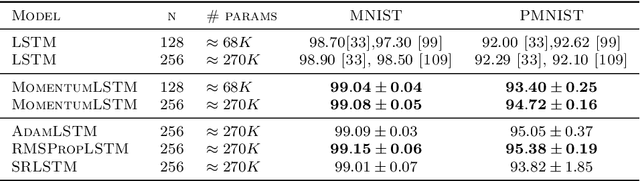
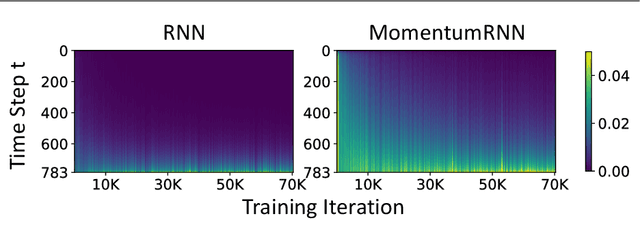
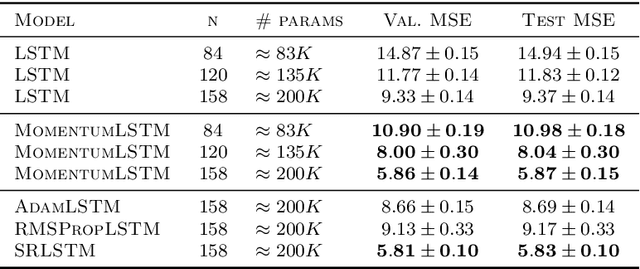
We present and review an algorithmic and theoretical framework for improving neural network architecture design via momentum. As case studies, we consider how momentum can improve the architecture design for recurrent neural networks (RNNs), neural ordinary differential equations (ODEs), and transformers. We show that integrating momentum into neural network architectures has several remarkable theoretical and empirical benefits, including 1) integrating momentum into RNNs and neural ODEs can overcome the vanishing gradient issues in training RNNs and neural ODEs, resulting in effective learning long-term dependencies. 2) momentum in neural ODEs can reduce the stiffness of the ODE dynamics, which significantly enhances the computational efficiency in training and testing. 3) momentum can improve the efficiency and accuracy of transformers.

Training Deep Neural Networks with Adaptive Momentum Inspired by the Quadratic Optimization

Heavy ball momentum is crucial in accelerating (stochastic) gradient-based optimization algorithms for machine learning. Existing heavy ball momentum is usually weighted by a uniform hyperparameter, which relies on excessive tuning. Moreover, the calibrated fixed hyperparameter may not lead to optimal performance. In this paper, to eliminate the effort for tuning the momentum-related hyperparameter, we propose a new adaptive momentum inspired by the optimal choice of the heavy ball momentum for quadratic optimization. Our proposed adaptive heavy ball momentum can improve stochastic gradient descent (SGD) and Adam. SGD and Adam with the newly designed adaptive momentum are more robust to large learning rates, converge faster, and generalize better than the baselines. We verify the efficiency of SGD and Adam with the new adaptive momentum on extensive machine learning benchmarks, including image classification, language modeling, and machine translation. Finally, we provide convergence guarantees for SGD and Adam with the proposed adaptive momentum.