Improving Flow Matching by Aligning Flow Divergence

Conditional flow matching (CFM) stands out as an efficient, simulation-free approach for training flow-based generative models, achieving remarkable performance for data generation. However, CFM is insufficient to ensure accuracy in learning probability paths. In this paper, we introduce a new partial differential equation characterization for the error between the learned and exact probability paths, along with its solution. We show that the total variation gap between the two probability paths is bounded above by a combination of the CFM loss and an associated divergence loss. This theoretical insight leads to the design of a new objective function that simultaneously matches the flow and its divergence. Our new approach improves the performance of the flow-based generative model by a noticeable margin without sacrificing generation efficiency. We showcase the advantages of this enhanced training approach over CFM on several important benchmark tasks, including generative modeling for dynamical systems, DNA sequences, and videos. Code is available at \href{https://github.com/Utah-Math-Data-Science/Flow_Div_Matching}{Utah-Math-Data-Science}.

RMFlow: Refined Mean Flow by a Noise-Injection Step for Multimodal Generation

Mean flow (MeanFlow) enables efficient, high-fidelity image generation, yet its single-function evaluation (1-NFE) generation often cannot yield compelling results. We address this issue by introducing RMFlow, an efficient multimodal generative model that integrates a coarse 1-NFE MeanFlow transport with a subsequent tailored noise-injection refinement step. RMFlow approximates the average velocity of the flow path using a neural network trained with a new loss function that balances minimizing the Wasserstein distance between probability paths and maximizing sample likelihood. RMFlow achieves near state-of-the-art results on text-to-image, context-to-molecule, and time-series generation using only 1-NFE, at a computational cost comparable to the baseline MeanFlows.

Towards Multiscale Graph-based Protein Learning with Geometric Secondary Structural Motifs

Graph neural networks (GNNs) have emerged as powerful tools for learning protein structures by capturing spatial relationships at the residue level. However, existing GNN-based methods often face challenges in learning multiscale representations and modeling long-range dependencies efficiently. In this work, we propose an efficient multiscale graph-based learning framework tailored to proteins. Our proposed framework contains two crucial components: (1) It constructs a hierarchical graph representation comprising a collection of fine-grained subgraphs, each corresponding to a secondary structure motif (e.g., $α$-helices, $β$-strands, loops), and a single coarse-grained graph that connects these motifs based on their spatial arrangement and relative orientation. (2) It employs two GNNs for feature learning: the first operates within individual secondary motifs to capture local interactions, and the second models higher-level structural relationships across motifs. Our modular framework allows a flexible choice of GNN in each stage. Theoretically, we show that our hierarchical framework preserves the desired maximal expressiveness, ensuring no loss of critical structural information. Empirically, we demonstrate that integrating baseline GNNs into our multiscale framework remarkably improves prediction accuracy and reduces computational cost across various benchmarks.

Learning to Control the Smoothness of Graph Convolutional Network Features

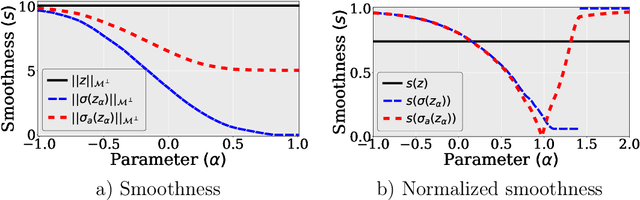
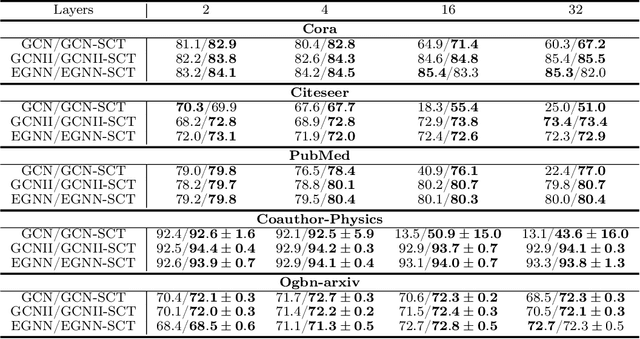
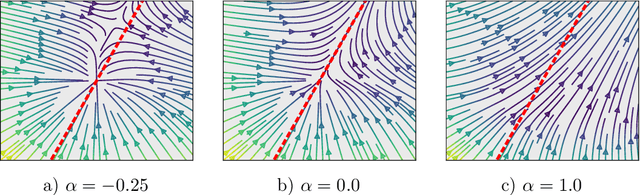
The pioneering work of Oono and Suzuki [ICLR, 2020] and Cai and Wang [arXiv:2006.13318] initializes the analysis of the smoothness of graph convolutional network (GCN) features. Their results reveal an intricate empirical correlation between node classification accuracy and the ratio of smooth to non-smooth feature components. However, the optimal ratio that favors node classification is unknown, and the non-smooth features of deep GCN with ReLU or leaky ReLU activation function diminish. In this paper, we propose a new strategy to let GCN learn node features with a desired smoothness -- adapting to data and tasks -- to enhance node classification. Our approach has three key steps: (1) We establish a geometric relationship between the input and output of ReLU or leaky ReLU. (2) Building on our geometric insights, we augment the message-passing process of graph convolutional layers (GCLs) with a learnable term to modulate the smoothness of node features with computational efficiency. (3) We investigate the achievable ratio between smooth and non-smooth feature components for GCNs with the augmented message-passing scheme. Our extensive numerical results show that the augmented message-passing schemes significantly improve node classification for GCN and some related models.