LlaMADRS: Prompting Large Language Models for Interview-Based Depression Assessment

This study introduces LlaMADRS, a novel framework leveraging open-source Large Language Models (LLMs) to automate depression severity assessment using the Montgomery-Asberg Depression Rating Scale (MADRS). We employ a zero-shot prompting strategy with carefully designed cues to guide the model in interpreting and scoring transcribed clinical interviews. Our approach, tested on 236 real-world interviews from the Context-Adaptive Multimodal Informatics (CAMI) dataset, demonstrates strong correlations with clinician assessments. The Qwen 2.5--72b model achieves near-human level agreement across most MADRS items, with Intraclass Correlation Coefficients (ICC) closely approaching those between human raters. We provide a comprehensive analysis of model performance across different MADRS items, highlighting strengths and current limitations. Our findings suggest that LLMs, with appropriate prompting, can serve as efficient tools for mental health assessment, potentially increasing accessibility in resource-limited settings. However, challenges remain, particularly in assessing symptoms that rely on non-verbal cues, underscoring the need for multimodal approaches in future work.

Learning to Control the Smoothness of Graph Convolutional Network Features

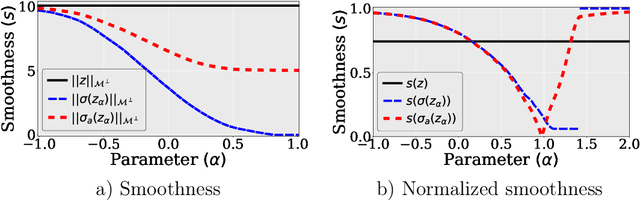
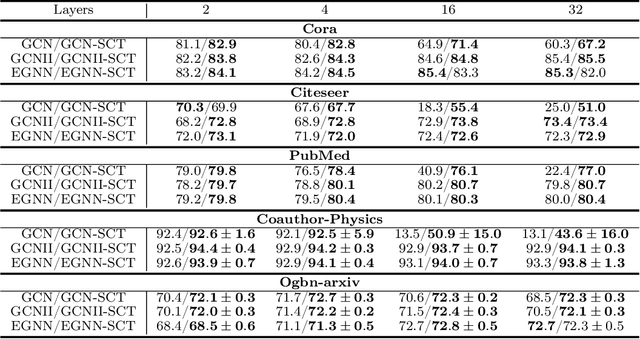
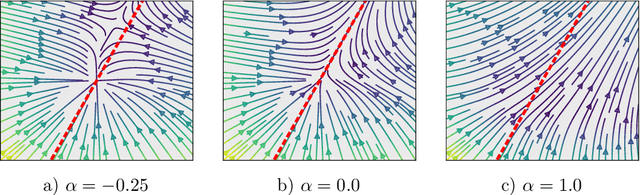
The pioneering work of Oono and Suzuki [ICLR, 2020] and Cai and Wang [arXiv:2006.13318] initializes the analysis of the smoothness of graph convolutional network (GCN) features. Their results reveal an intricate empirical correlation between node classification accuracy and the ratio of smooth to non-smooth feature components. However, the optimal ratio that favors node classification is unknown, and the non-smooth features of deep GCN with ReLU or leaky ReLU activation function diminish. In this paper, we propose a new strategy to let GCN learn node features with a desired smoothness -- adapting to data and tasks -- to enhance node classification. Our approach has three key steps: (1) We establish a geometric relationship between the input and output of ReLU or leaky ReLU. (2) Building on our geometric insights, we augment the message-passing process of graph convolutional layers (GCLs) with a learnable term to modulate the smoothness of node features with computational efficiency. (3) We investigate the achievable ratio between smooth and non-smooth feature components for GCNs with the augmented message-passing scheme. Our extensive numerical results show that the augmented message-passing schemes significantly improve node classification for GCN and some related models.

Proximal Implicit ODE Solvers for Accelerating Learning Neural ODEs

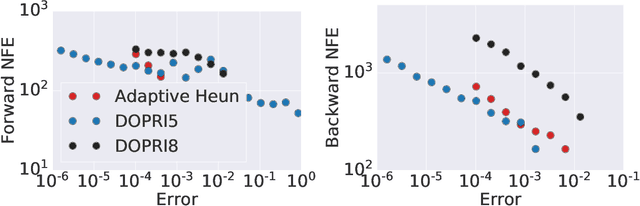
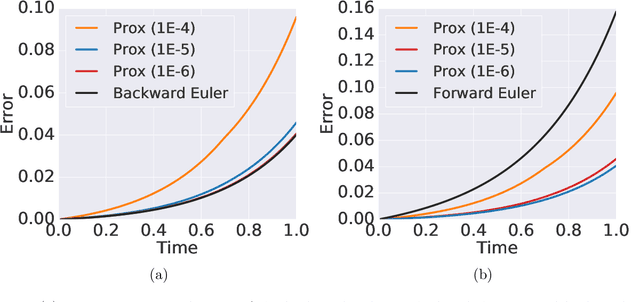
Learning neural ODEs often requires solving very stiff ODE systems, primarily using explicit adaptive step size ODE solvers. These solvers are computationally expensive, requiring the use of tiny step sizes for numerical stability and accuracy guarantees. This paper considers learning neural ODEs using implicit ODE solvers of different orders leveraging proximal operators. The proximal implicit solver consists of inner-outer iterations: the inner iterations approximate each implicit update step using a fast optimization algorithm, and the outer iterations solve the ODE system over time. The proximal implicit ODE solver guarantees superiority over explicit solvers in numerical stability and computational efficiency. We validate the advantages of proximal implicit solvers over existing popular neural ODE solvers on various challenging benchmark tasks, including learning continuous-depth graph neural networks and continuous normalizing flows.

Learning POD of Complex Dynamics Using Heavy-ball Neural ODEs

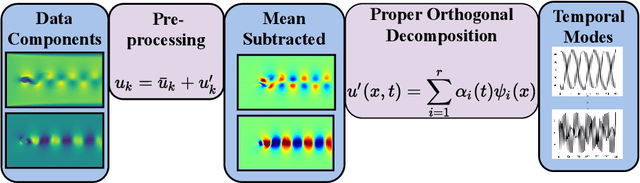
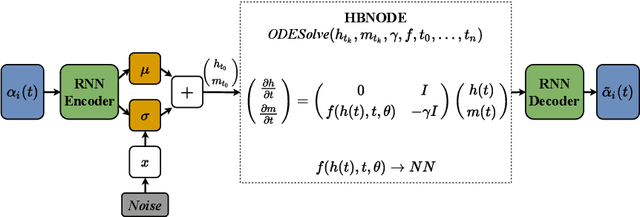
Proper orthogonal decomposition (POD) allows reduced-order modeling of complex dynamical systems at a substantial level, while maintaining a high degree of accuracy in modeling the underlying dynamical systems. Advances in machine learning algorithms enable learning POD-based dynamics from data and making accurate and fast predictions of dynamical systems. In this paper, we leverage the recently proposed heavy-ball neural ODEs (HBNODEs) [Xia et al. NeurIPS, 2021] for learning data-driven reduced-order models (ROMs) in the POD context, in particular, for learning dynamics of time-varying coefficients generated by the POD analysis on training snapshots generated from solving full order models. HBNODE enjoys several practical advantages for learning POD-based ROMs with theoretical guarantees, including 1) HBNODE can learn long-term dependencies effectively from sequential observations and 2) HBNODE is computationally efficient in both training and testing. We compare HBNODE with other popular ROMs on several complex dynamical systems, including the von K\'{a}rm\'{a}n Street flow, the Kurganov-Petrova-Popov equation, and the one-dimensional Euler equations for fluids modeling.