Proximal Implicit ODE Solvers for Accelerating Learning Neural ODEs
Paper and Code
Apr 19, 2022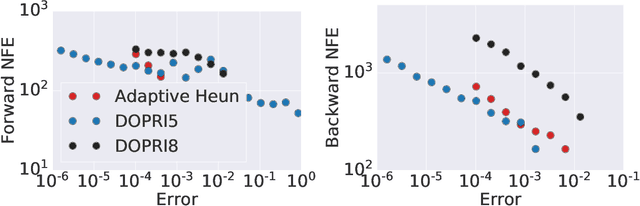

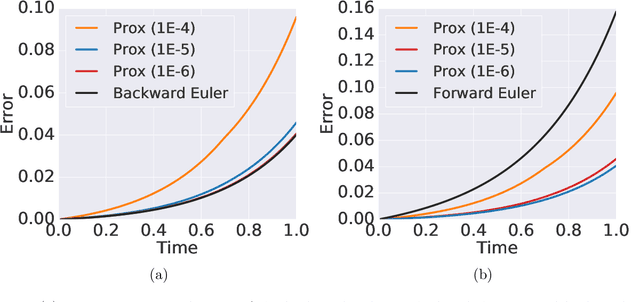

Learning neural ODEs often requires solving very stiff ODE systems, primarily using explicit adaptive step size ODE solvers. These solvers are computationally expensive, requiring the use of tiny step sizes for numerical stability and accuracy guarantees. This paper considers learning neural ODEs using implicit ODE solvers of different orders leveraging proximal operators. The proximal implicit solver consists of inner-outer iterations: the inner iterations approximate each implicit update step using a fast optimization algorithm, and the outer iterations solve the ODE system over time. The proximal implicit ODE solver guarantees superiority over explicit solvers in numerical stability and computational efficiency. We validate the advantages of proximal implicit solvers over existing popular neural ODE solvers on various challenging benchmark tasks, including learning continuous-depth graph neural networks and continuous normalizing flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge