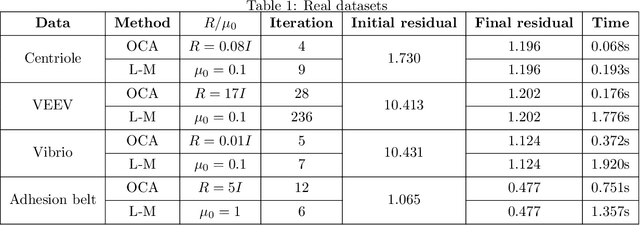
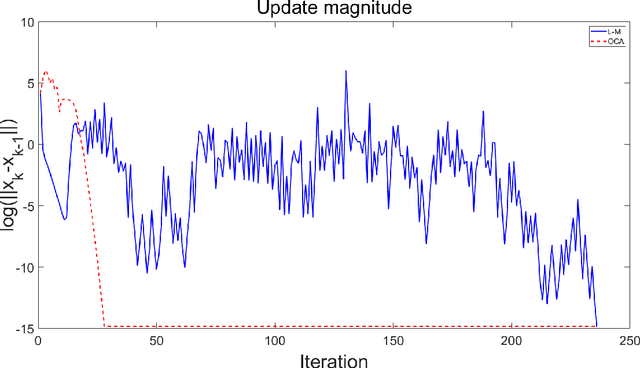
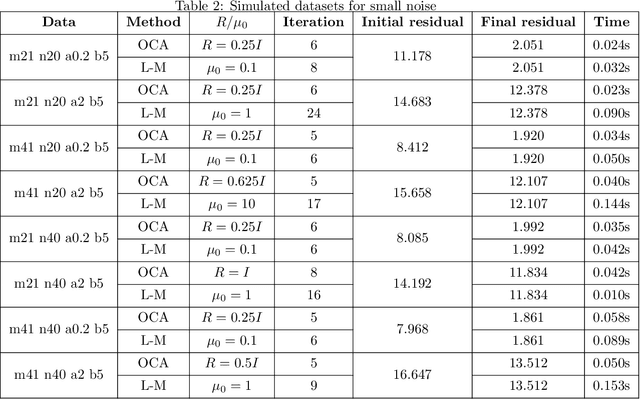
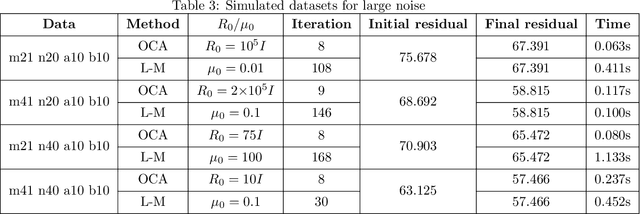
A novel algorithm for optimizing bundle adjustment in image sequence alignment

The Bundle Adjustment (BA) model is commonly optimized using a nonlinear least squares method, with the Levenberg-Marquardt (L-M) algorithm being a typical choice. However, despite the L-M algorithm's effectiveness, its sensitivity to initial conditions often results in slower convergence when applied to poorly conditioned datasets, motivating the exploration of alternative optimization strategies. This paper introduces a novel algorithm for optimizing the BA model in the context of image sequence alignment for cryo-electron tomography, utilizing optimal control theory to directly optimize general nonlinear functions. The proposed Optimal Control Algorithm (OCA) exhibits superior convergence rates and effectively mitigates the oscillatory behavior frequently observed in L-M algorithm. Extensive experiments on both synthetic and real-world datasets were conducted to evaluate the algorithm's performance. The results demonstrate that the OCA achieves faster convergence compared to the L-M algorithm. Moreover, the incorporation of a bisection-based update procedure significantly enhances the OCA's performance, particularly in poorly initialized datasets. These findings indicate that the OCA can substantially improve the efficiency of 3D reconstructions in cryo-electron tomography.

TVG: A Training-free Transition Video Generation Method with Diffusion Models

Transition videos play a crucial role in media production, enhancing the flow and coherence of visual narratives. Traditional methods like morphing often lack artistic appeal and require specialized skills, limiting their effectiveness. Recent advances in diffusion model-based video generation offer new possibilities for creating transitions but face challenges such as poor inter-frame relationship modeling and abrupt content changes. We propose a novel training-free Transition Video Generation (TVG) approach using video-level diffusion models that addresses these limitations without additional training. Our method leverages Gaussian Process Regression ($\mathcal{GPR}$) to model latent representations, ensuring smooth and dynamic transitions between frames. Additionally, we introduce interpolation-based conditional controls and a Frequency-aware Bidirectional Fusion (FBiF) architecture to enhance temporal control and transition reliability. Evaluations of benchmark datasets and custom image pairs demonstrate the effectiveness of our approach in generating high-quality smooth transition videos. The code are provided in https://sobeymil.github.io/tvg.com.

A Unified Plug-and-Play Algorithm with Projected Landweber Operator for Split Convex Feasibility Problems

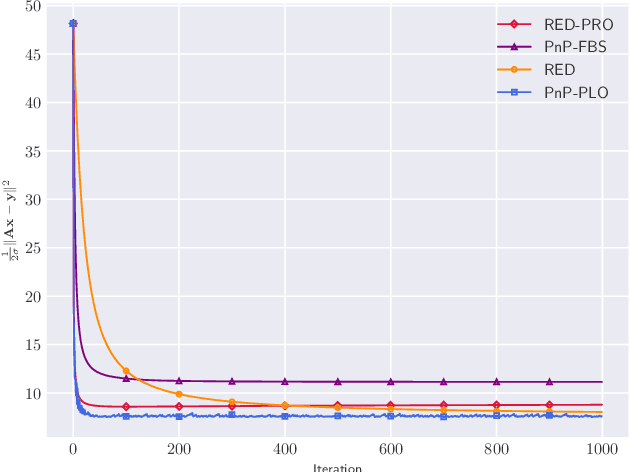
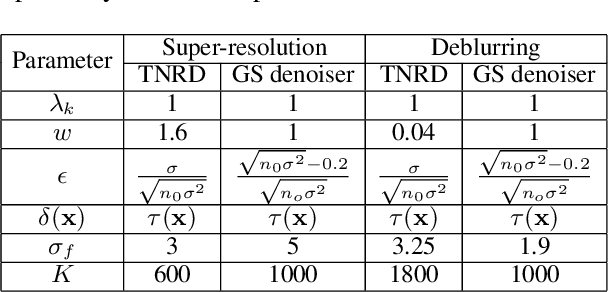
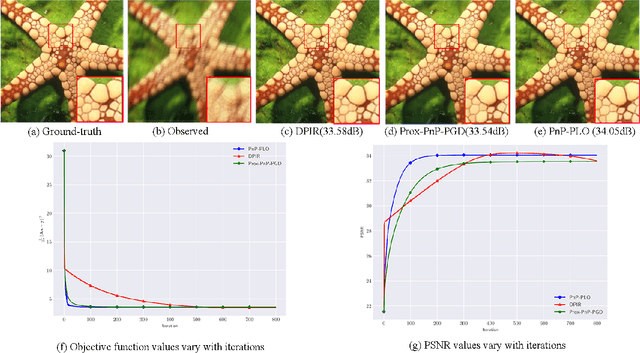
In recent years Plug-and-Play (PnP) methods have achieved state-of-the-art performance in inverse imaging problems by replacing proximal operators with denoisers. Based on the proximal gradient method, some theoretical results of PnP have appeared, where appropriate step size is crucial for convergence analysis. However, in practical applications, applying PnP methods with theoretically guaranteed step sizes is difficult, and these algorithms are limited to Gaussian noise. In this paper,from a perspective of split convex feasibility problems (SCFP), an adaptive PnP algorithm with Projected Landweber Operator (PnP-PLO) is proposed to address these issues. Numerical experiments on image deblurring, super-resolution, and compressed sensing MRI experiments illustrate that PnP-PLO with theoretical guarantees outperforms state-of-the-art methods such as RED and RED-PRO.

HPPP: Halpern-type Preconditioned Proximal Point Algorithms and Applications to Image Restoration

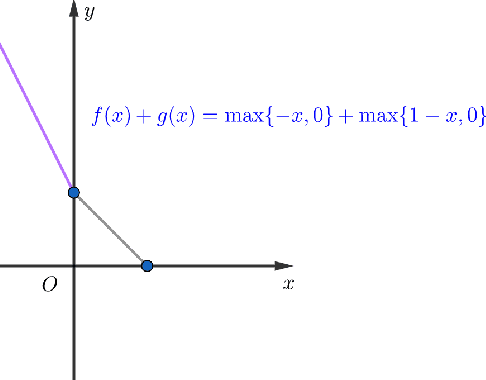
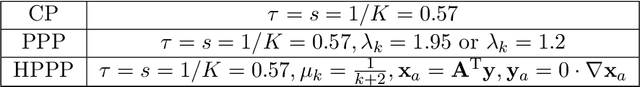
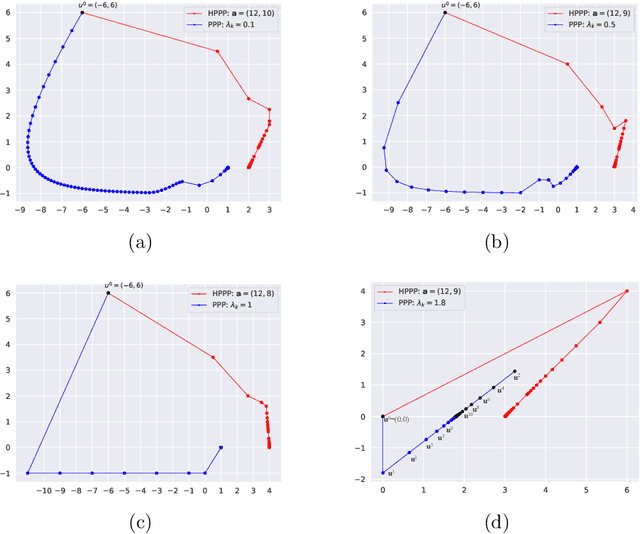
Preconditioned Proximal Point (PPP) algorithms provide a unified framework for splitting methods in image restoration. Recent advancements with RED (Regularization by Denoising) and PnP (Plug-and-Play) priors have achieved state-of-the-art performance in this domain, emphasizing the need for a meaningful particular solution. However, degenerate PPP algorithms typically exhibit weak convergence in infinite-dimensional Hilbert space, leading to uncertain solutions. To address this issue, we propose the Halpern-type Preconditioned Proximal Point (HPPP) algorithm, which leverages the strong convergence properties of Halpern iteration to achieve a particular solution. Based on the implicit regularization defined by gradient RED, we further introduce the Gradient REgularization by Denoising via HPPP called GraRED-HP3 algorithm. The HPPP algorithm is shown to have the regularity converging to a particular solution by a toy example. Additionally, experiments in image deblurring and inpainting validate the effectiveness of GraRED-HP3, showing it surpasses classical methods such as Chambolle-Pock (CP), PPP, RED, and RED-PRO.

UMMAFormer: A Universal Multimodal-adaptive Transformer Framework for Temporal Forgery Localization

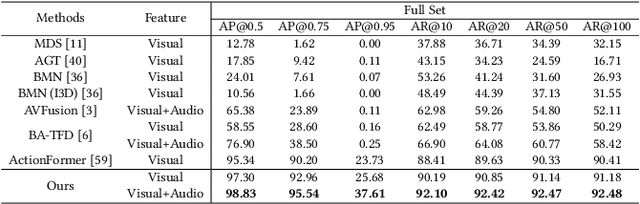
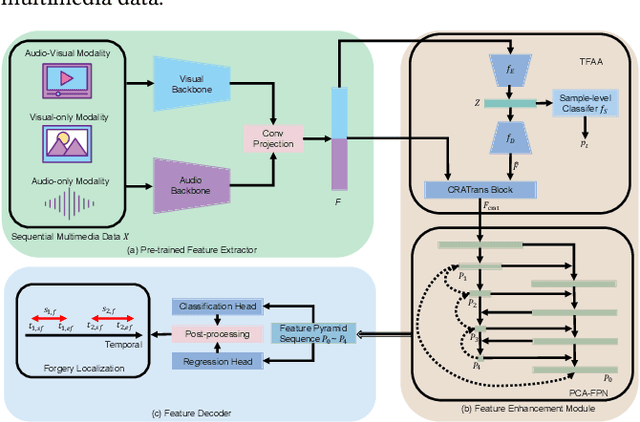
The emergence of artificial intelligence-generated content (AIGC) has raised concerns about the authenticity of multimedia content in various fields. However, existing research for forgery content detection has focused mainly on binary classification tasks of complete videos, which has limited applicability in industrial settings. To address this gap, we propose UMMAFormer, a novel universal transformer framework for temporal forgery localization (TFL) that predicts forgery segments with multimodal adaptation. Our approach introduces a Temporal Feature Abnormal Attention (TFAA) module based on temporal feature reconstruction to enhance the detection of temporal differences. We also design a Parallel Cross-Attention Feature Pyramid Network (PCA-FPN) to optimize the Feature Pyramid Network (FPN) for subtle feature enhancement. To evaluate the proposed method, we contribute a novel Temporal Video Inpainting Localization (TVIL) dataset specifically tailored for video inpainting scenes. Our experiments show that our approach achieves state-of-the-art performance on benchmark datasets, including Lav-DF, TVIL, and Psynd, significantly outperforming previous methods. The code and data are available at https://github.com/ymhzyj/UMMAFormer/.

Phase Retrieval with Background Information: Decreased References and Efficient Methods

Fourier phase retrieval(PR) is a severely ill-posed inverse problem that arises in various applications. To guarantee a unique solution and relieve the dependence on the initialization, background information can be exploited as a structural priors. However, the requirement for the background information may be challenging when moving to the high-resolution imaging. At the same time, the previously proposed projected gradient descent(PGD) method also demands much background information. In this paper, we present an improved theoretical result about the demand for the background information, along with two Douglas Rachford(DR) based methods. Analytically, we demonstrate that the background required to ensure a unique solution can be decreased by nearly $1/2$ for the 2-D signals compared to the 1-D signals. By generalizing the results into $d$-dimension, we show that the length of the background information more than $(2^{\frac{d+1}{d}}-1)$ folds of the signal is sufficient to ensure the uniqueness. At the same time, we also analyze the stability and robustness of the model when measurements and background information are corrupted by the noise. Furthermore, two methods called Background Douglas-Rachford (BDR) and Convex Background Douglas-Rachford (CBDR) are proposed. BDR which is a kind of non-convex method is proven to have the local R-linear convergence rate under mild assumptions. Instead, CBDR method uses the techniques of convexification and can be proven to own a global convergence guarantee as long as the background information is sufficient. To support this, a new property called F-RIP is established. We test the performance of the proposed methods through simulations as well as real experimental measurements, and demonstrate that they achieve a higher recovery rate with less background information compared to the PGD method.

Untrained neural network embedded Fourier phase retrieval from few measurements

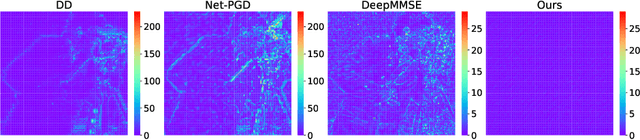
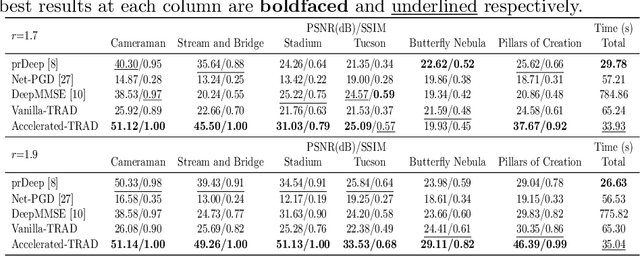
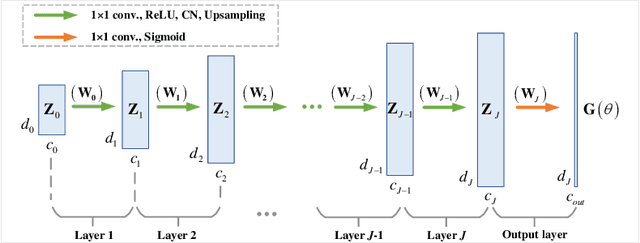
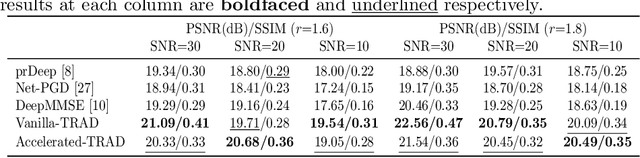
Fourier phase retrieval (FPR) is a challenging task widely used in various applications. It involves recovering an unknown signal from its Fourier phaseless measurements. FPR with few measurements is important for reducing time and hardware costs, but it suffers from serious ill-posedness. Recently, untrained neural networks have offered new approaches by introducing learned priors to alleviate the ill-posedness without requiring any external data. However, they may not be ideal for reconstructing fine details in images and can be computationally expensive. This paper proposes an untrained neural network (NN) embedded algorithm based on the alternating direction method of multipliers (ADMM) framework to solve FPR with few measurements. Specifically, we use a generative network to represent the image to be recovered, which confines the image to the space defined by the network structure. To improve the ability to represent high-frequency information, total variation (TV) regularization is imposed to facilitate the recovery of local structures in the image. Furthermore, to reduce the computational cost mainly caused by the parameter updates of the untrained NN, we develop an accelerated algorithm that adaptively trades off between explicit and implicit regularization. Experimental results indicate that the proposed algorithm outperforms existing untrained NN-based algorithms with fewer computational resources and even performs competitively against trained NN-based algorithms.

Regularize implicit neural representation by itself

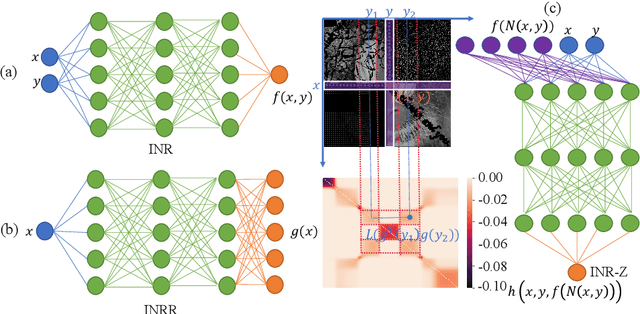
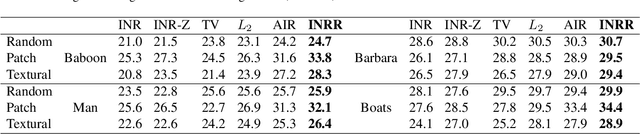
This paper proposes a regularizer called Implicit Neural Representation Regularizer (INRR) to improve the generalization ability of the Implicit Neural Representation (INR). The INR is a fully connected network that can represent signals with details not restricted by grid resolution. However, its generalization ability could be improved, especially with non-uniformly sampled data. The proposed INRR is based on learned Dirichlet Energy (DE) that measures similarities between rows/columns of the matrix. The smoothness of the Laplacian matrix is further integrated by parameterizing DE with a tiny INR. INRR improves the generalization of INR in signal representation by perfectly integrating the signal's self-similarity with the smoothness of the Laplacian matrix. Through well-designed numerical experiments, the paper also reveals a series of properties derived from INRR, including momentum methods like convergence trajectory and multi-scale similarity. Moreover, the proposed method could improve the performance of other signal representation methods.

ADMM based Fourier phase retrieval with untrained generative prior

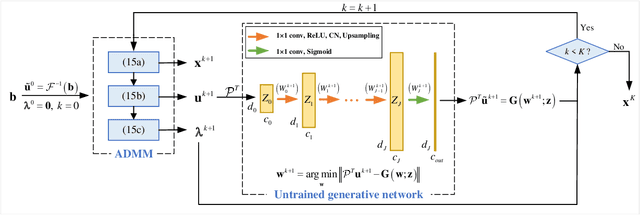
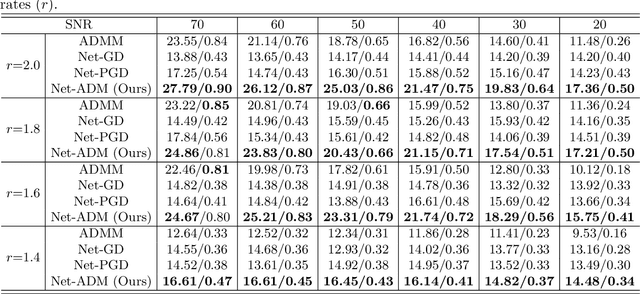
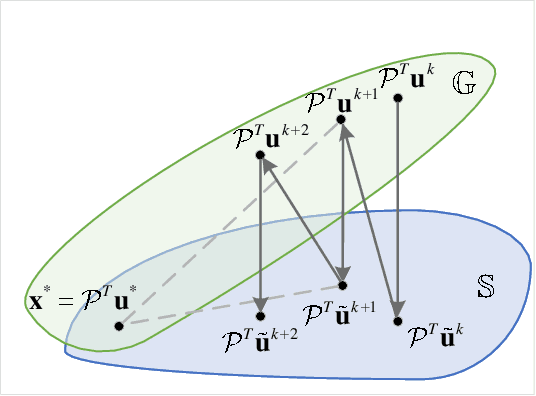
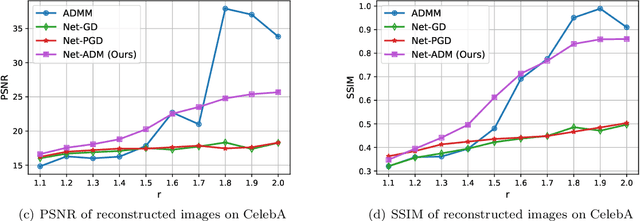
Fourier phase retrieval (FPR) is an inverse problem that recovers the signal from its Fourier magnitude measurement, it's ill-posed especially when the sampling rates are low. In this paper, an untrained generative prior is introduced to attack the ill-posedness. Based on the alternating direction method of multipliers (ADMM), an algorithm utilizing the untrained generative network called Net-ADM is proposed to solve the FPR problem. Firstly, the objective function is smoothed and the dimension of the variable is raised to facilitate calculation. Then an untrained generative network is embedded in the iterative process of ADMM to project an estimated signal into the generative space, and the projected signal is applied to next iteration of ADMM. We theoretically analyzed the two projections included in the algorithm, one makes the objective function descent, and the other gets the estimation closer to the optimal solution. Numerical experiments show that the reconstruction performance and robustness of the proposed algorithm are superior to prior works, especially when the sampling rates are low.

Adaptive and Implicit Regularization for Matrix Completion

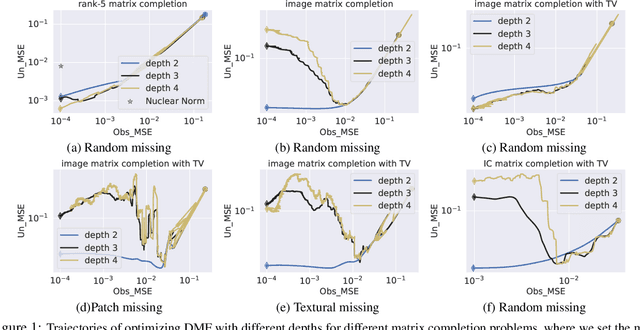
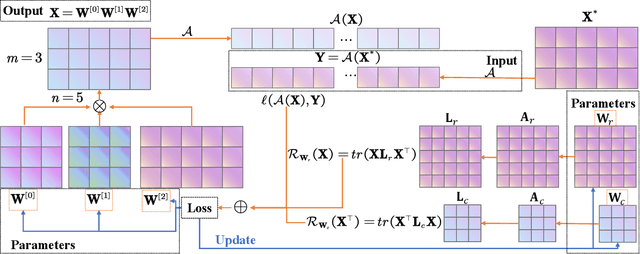
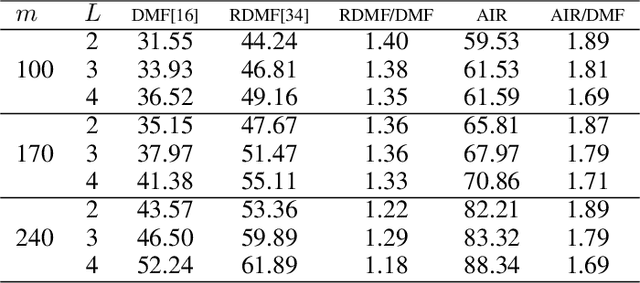
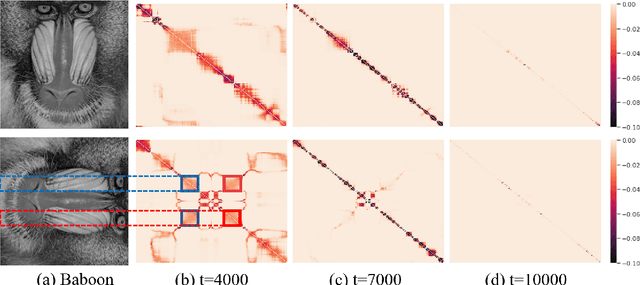
The explicit low-rank regularization, e.g., nuclear norm regularization, has been widely used in imaging sciences. However, it has been found that implicit regularization outperforms explicit ones in various image processing tasks. Another issue is that the fixed explicit regularization limits the applicability to broad images since different images favor different features captured by different explicit regularizations. As such, this paper proposes a new adaptive and implicit low-rank regularization that captures the low-rank prior dynamically from the training data. The core of our new adaptive and implicit low-rank regularization is parameterizing the Laplacian matrix in the Dirichlet energy-based regularization, which we call the regularization AIR. Theoretically, we show that the adaptive regularization of \ReTwo{AIR} enhances the implicit regularization and vanishes at the end of training. We validate AIR's effectiveness on various benchmark tasks, indicating that the AIR is particularly favorable for the scenarios when the missing entries are non-uniform. The code can be found at https://github.com/lizhemin15/AIR-Net.