Untrained neural network embedded Fourier phase retrieval from few measurements
Paper and Code
Jul 16, 2023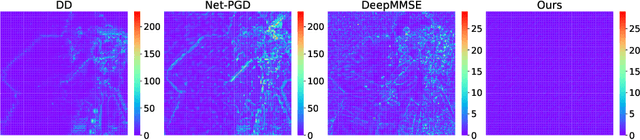
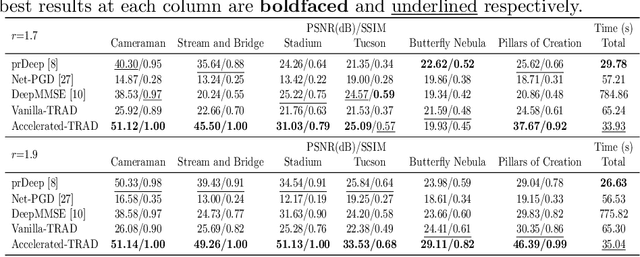
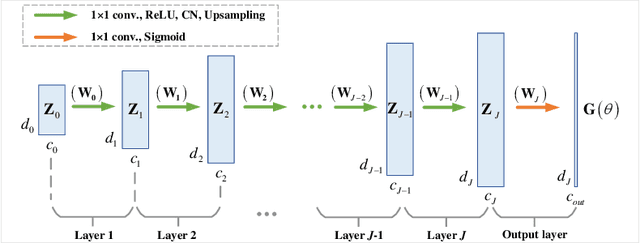
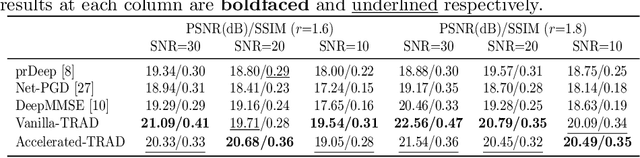
Fourier phase retrieval (FPR) is a challenging task widely used in various applications. It involves recovering an unknown signal from its Fourier phaseless measurements. FPR with few measurements is important for reducing time and hardware costs, but it suffers from serious ill-posedness. Recently, untrained neural networks have offered new approaches by introducing learned priors to alleviate the ill-posedness without requiring any external data. However, they may not be ideal for reconstructing fine details in images and can be computationally expensive. This paper proposes an untrained neural network (NN) embedded algorithm based on the alternating direction method of multipliers (ADMM) framework to solve FPR with few measurements. Specifically, we use a generative network to represent the image to be recovered, which confines the image to the space defined by the network structure. To improve the ability to represent high-frequency information, total variation (TV) regularization is imposed to facilitate the recovery of local structures in the image. Furthermore, to reduce the computational cost mainly caused by the parameter updates of the untrained NN, we develop an accelerated algorithm that adaptively trades off between explicit and implicit regularization. Experimental results indicate that the proposed algorithm outperforms existing untrained NN-based algorithms with fewer computational resources and even performs competitively against trained NN-based algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge