Phase Retrieval with Background Information: Decreased References and Efficient Methods

Fourier phase retrieval(PR) is a severely ill-posed inverse problem that arises in various applications. To guarantee a unique solution and relieve the dependence on the initialization, background information can be exploited as a structural priors. However, the requirement for the background information may be challenging when moving to the high-resolution imaging. At the same time, the previously proposed projected gradient descent(PGD) method also demands much background information. In this paper, we present an improved theoretical result about the demand for the background information, along with two Douglas Rachford(DR) based methods. Analytically, we demonstrate that the background required to ensure a unique solution can be decreased by nearly $1/2$ for the 2-D signals compared to the 1-D signals. By generalizing the results into $d$-dimension, we show that the length of the background information more than $(2^{\frac{d+1}{d}}-1)$ folds of the signal is sufficient to ensure the uniqueness. At the same time, we also analyze the stability and robustness of the model when measurements and background information are corrupted by the noise. Furthermore, two methods called Background Douglas-Rachford (BDR) and Convex Background Douglas-Rachford (CBDR) are proposed. BDR which is a kind of non-convex method is proven to have the local R-linear convergence rate under mild assumptions. Instead, CBDR method uses the techniques of convexification and can be proven to own a global convergence guarantee as long as the background information is sufficient. To support this, a new property called F-RIP is established. We test the performance of the proposed methods through simulations as well as real experimental measurements, and demonstrate that they achieve a higher recovery rate with less background information compared to the PGD method.

Untrained neural network embedded Fourier phase retrieval from few measurements

Fourier phase retrieval (FPR) is a challenging task widely used in various applications. It involves recovering an unknown signal from its Fourier phaseless measurements. FPR with few measurements is important for reducing time and hardware costs, but it suffers from serious ill-posedness. Recently, untrained neural networks have offered new approaches by introducing learned priors to alleviate the ill-posedness without requiring any external data. However, they may not be ideal for reconstructing fine details in images and can be computationally expensive. This paper proposes an untrained neural network (NN) embedded algorithm based on the alternating direction method of multipliers (ADMM) framework to solve FPR with few measurements. Specifically, we use a generative network to represent the image to be recovered, which confines the image to the space defined by the network structure. To improve the ability to represent high-frequency information, total variation (TV) regularization is imposed to facilitate the recovery of local structures in the image. Furthermore, to reduce the computational cost mainly caused by the parameter updates of the untrained NN, we develop an accelerated algorithm that adaptively trades off between explicit and implicit regularization. Experimental results indicate that the proposed algorithm outperforms existing untrained NN-based algorithms with fewer computational resources and even performs competitively against trained NN-based algorithms.

ADMM based Fourier phase retrieval with untrained generative prior

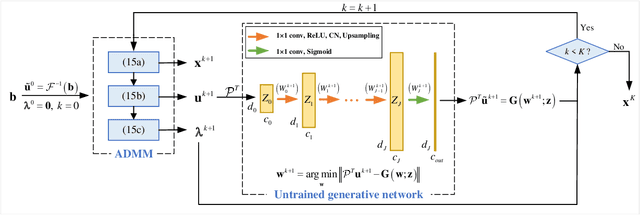
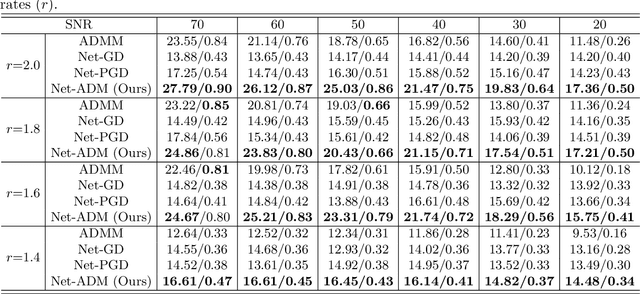
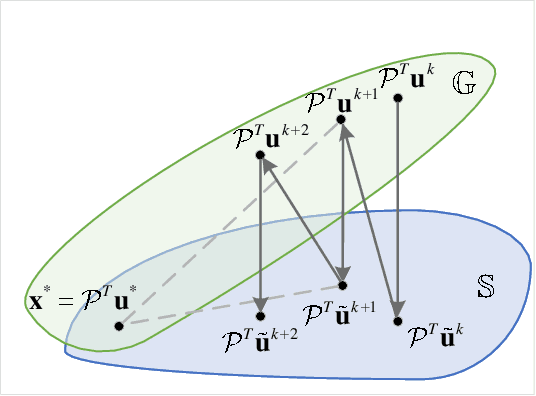
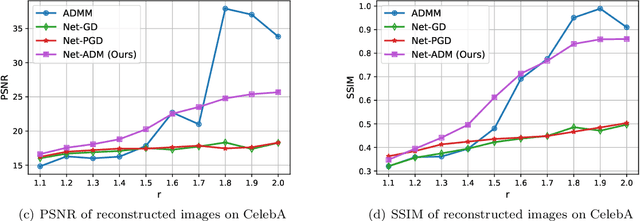
Fourier phase retrieval (FPR) is an inverse problem that recovers the signal from its Fourier magnitude measurement, it's ill-posed especially when the sampling rates are low. In this paper, an untrained generative prior is introduced to attack the ill-posedness. Based on the alternating direction method of multipliers (ADMM), an algorithm utilizing the untrained generative network called Net-ADM is proposed to solve the FPR problem. Firstly, the objective function is smoothed and the dimension of the variable is raised to facilitate calculation. Then an untrained generative network is embedded in the iterative process of ADMM to project an estimated signal into the generative space, and the projected signal is applied to next iteration of ADMM. We theoretically analyzed the two projections included in the algorithm, one makes the objective function descent, and the other gets the estimation closer to the optimal solution. Numerical experiments show that the reconstruction performance and robustness of the proposed algorithm are superior to prior works, especially when the sampling rates are low.