ADMM based Fourier phase retrieval with untrained generative prior
Paper and Code
Oct 23, 2022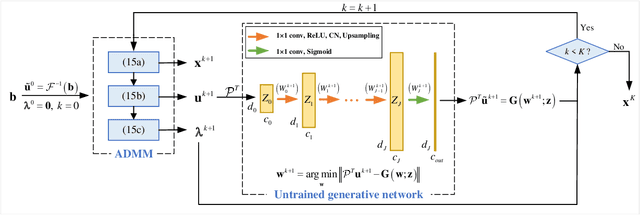
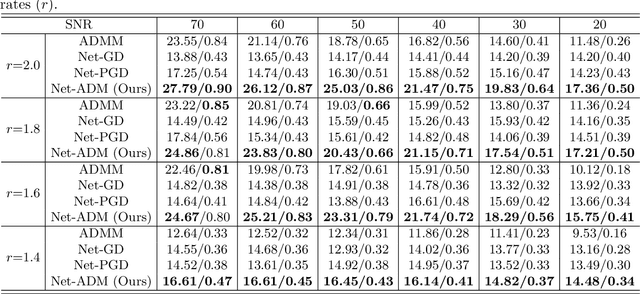
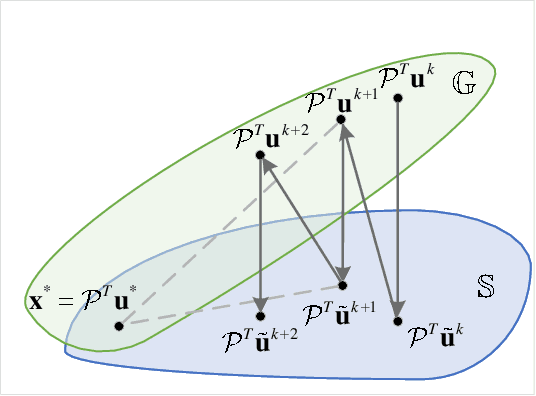
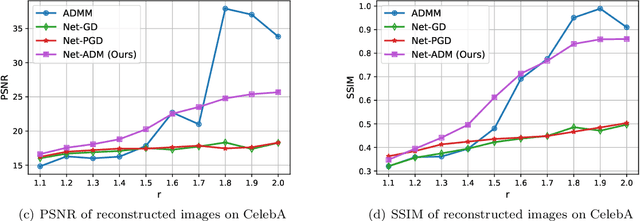
Fourier phase retrieval (FPR) is an inverse problem that recovers the signal from its Fourier magnitude measurement, it's ill-posed especially when the sampling rates are low. In this paper, an untrained generative prior is introduced to attack the ill-posedness. Based on the alternating direction method of multipliers (ADMM), an algorithm utilizing the untrained generative network called Net-ADM is proposed to solve the FPR problem. Firstly, the objective function is smoothed and the dimension of the variable is raised to facilitate calculation. Then an untrained generative network is embedded in the iterative process of ADMM to project an estimated signal into the generative space, and the projected signal is applied to next iteration of ADMM. We theoretically analyzed the two projections included in the algorithm, one makes the objective function descent, and the other gets the estimation closer to the optimal solution. Numerical experiments show that the reconstruction performance and robustness of the proposed algorithm are superior to prior works, especially when the sampling rates are low.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge