Regularize implicit neural representation by itself

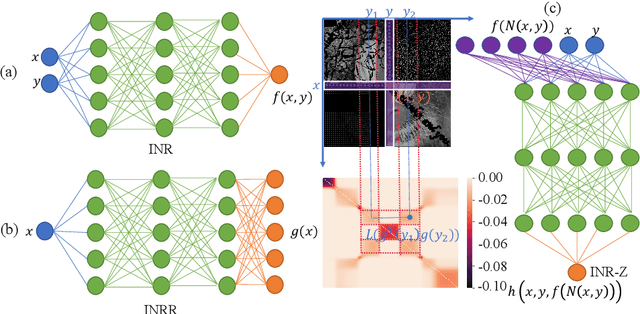
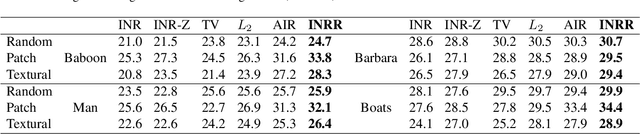
This paper proposes a regularizer called Implicit Neural Representation Regularizer (INRR) to improve the generalization ability of the Implicit Neural Representation (INR). The INR is a fully connected network that can represent signals with details not restricted by grid resolution. However, its generalization ability could be improved, especially with non-uniformly sampled data. The proposed INRR is based on learned Dirichlet Energy (DE) that measures similarities between rows/columns of the matrix. The smoothness of the Laplacian matrix is further integrated by parameterizing DE with a tiny INR. INRR improves the generalization of INR in signal representation by perfectly integrating the signal's self-similarity with the smoothness of the Laplacian matrix. Through well-designed numerical experiments, the paper also reveals a series of properties derived from INRR, including momentum methods like convergence trajectory and multi-scale similarity. Moreover, the proposed method could improve the performance of other signal representation methods.

Low-Rank Tensor Function Representation for Multi-Dimensional Data Recovery

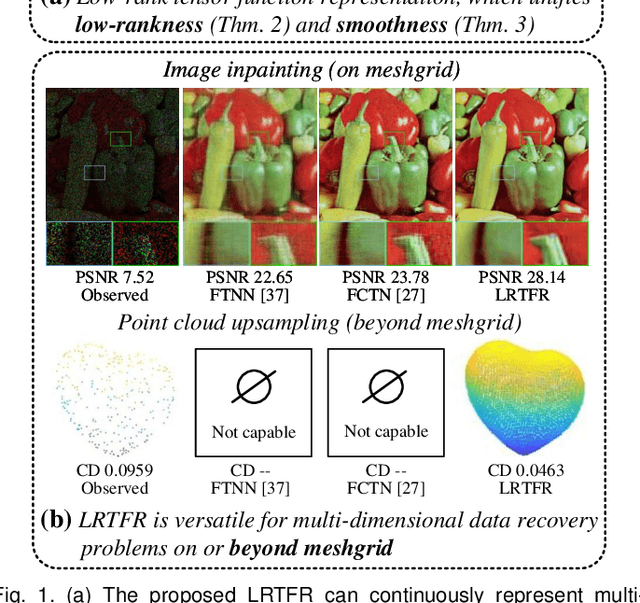
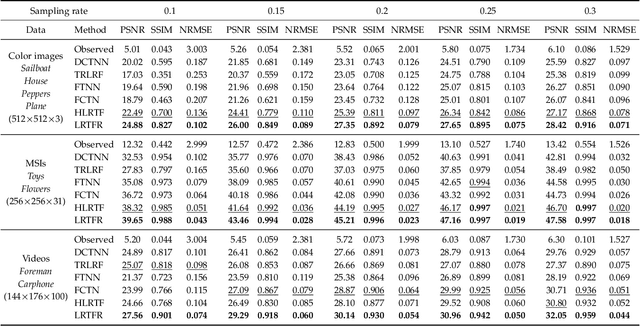
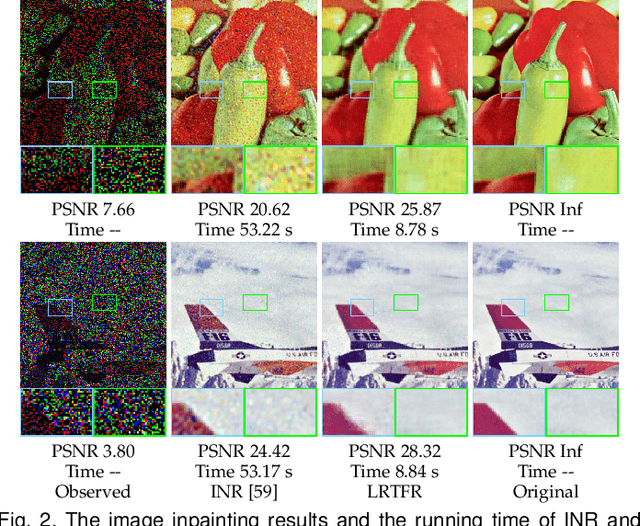
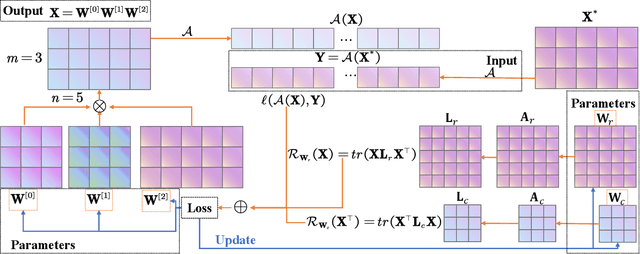
Since higher-order tensors are naturally suitable for representing multi-dimensional data in real-world, e.g., color images and videos, low-rank tensor representation has become one of the emerging areas in machine learning and computer vision. However, classical low-rank tensor representations can only represent data on finite meshgrid due to their intrinsical discrete nature, which hinders their potential applicability in many scenarios beyond meshgrid. To break this barrier, we propose a low-rank tensor function representation (LRTFR), which can continuously represent data beyond meshgrid with infinite resolution. Specifically, the suggested tensor function, which maps an arbitrary coordinate to the corresponding value, can continuously represent data in an infinite real space. Parallel to discrete tensors, we develop two fundamental concepts for tensor functions, i.e., the tensor function rank and low-rank tensor function factorization. We theoretically justify that both low-rank and smooth regularizations are harmoniously unified in the LRTFR, which leads to high effectiveness and efficiency for data continuous representation. Extensive multi-dimensional data recovery applications arising from image processing (image inpainting and denoising), machine learning (hyperparameter optimization), and computer graphics (point cloud upsampling) substantiate the superiority and versatility of our method as compared with state-of-the-art methods. Especially, the experiments beyond the original meshgrid resolution (hyperparameter optimization) or even beyond meshgrid (point cloud upsampling) validate the favorable performances of our method for continuous representation.

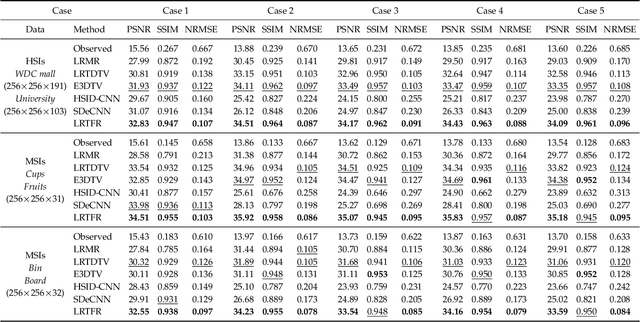
Adaptive and Implicit Regularization for Matrix Completion

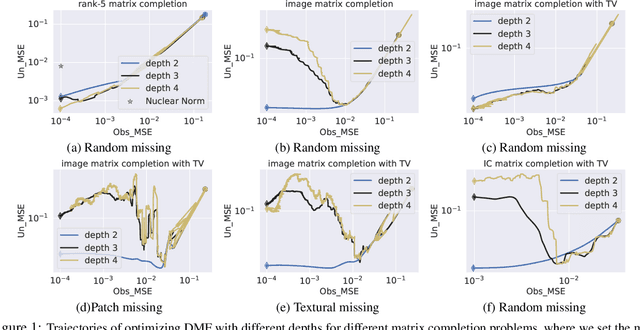
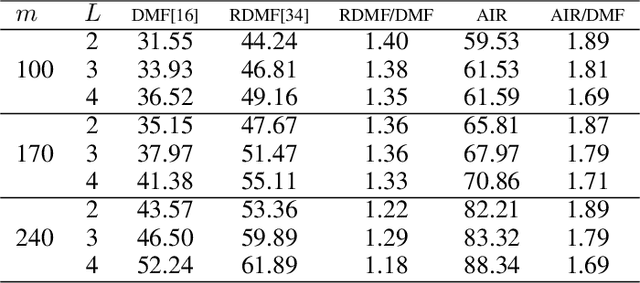
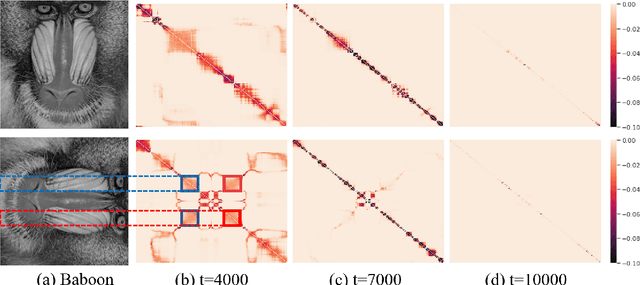
The explicit low-rank regularization, e.g., nuclear norm regularization, has been widely used in imaging sciences. However, it has been found that implicit regularization outperforms explicit ones in various image processing tasks. Another issue is that the fixed explicit regularization limits the applicability to broad images since different images favor different features captured by different explicit regularizations. As such, this paper proposes a new adaptive and implicit low-rank regularization that captures the low-rank prior dynamically from the training data. The core of our new adaptive and implicit low-rank regularization is parameterizing the Laplacian matrix in the Dirichlet energy-based regularization, which we call the regularization AIR. Theoretically, we show that the adaptive regularization of \ReTwo{AIR} enhances the implicit regularization and vanishes at the end of training. We validate AIR's effectiveness on various benchmark tasks, indicating that the AIR is particularly favorable for the scenarios when the missing entries are non-uniform. The code can be found at https://github.com/lizhemin15/AIR-Net.

AIR-Net: Adaptive and Implicit Regularization Neural Network for Matrix Completion

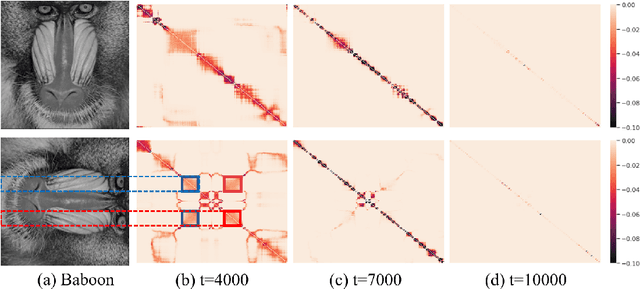
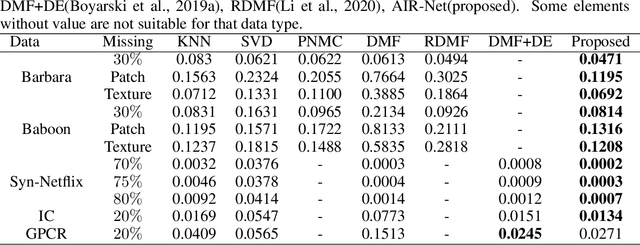
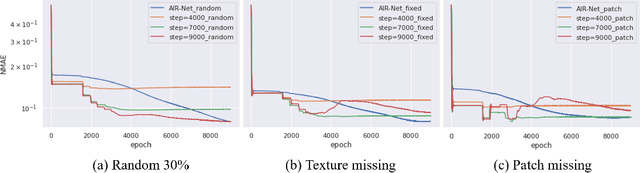
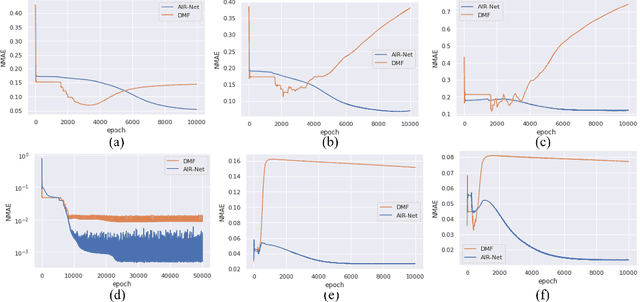
Conventionally, the matrix completion (MC) model aims to recover a matrix from partially observed elements. Accurate recovery necessarily requires a regularization encoding priors of the unknown matrix/signal properly. However, encoding the priors accurately for the complex natural signal is difficult, and even then, the model might not generalize well outside the particular matrix type. This work combines adaptive and implicit low-rank regularization that captures the prior dynamically according to the current recovered matrix. Furthermore, we aim to answer the question: how does adaptive regularization affect implicit regularization? We utilize neural networks to represent Adaptive and Implicit Regularization and named the proposed model \textit{AIR-Net}. Theoretical analyses show that the adaptive part of the AIR-Net enhances implicit regularization. In addition, the adaptive regularizer vanishes at the end, thus can avoid saturation issues. Numerical experiments for various data demonstrate the effectiveness of AIR-Net, especially when the locations of missing elements are not randomly chosen. With complete flexibility to select neural networks for matrix representation, AIR-Net can be extended to solve more general inverse problems.

A regularized deep matrix factorized model of matrix completion for image restoration

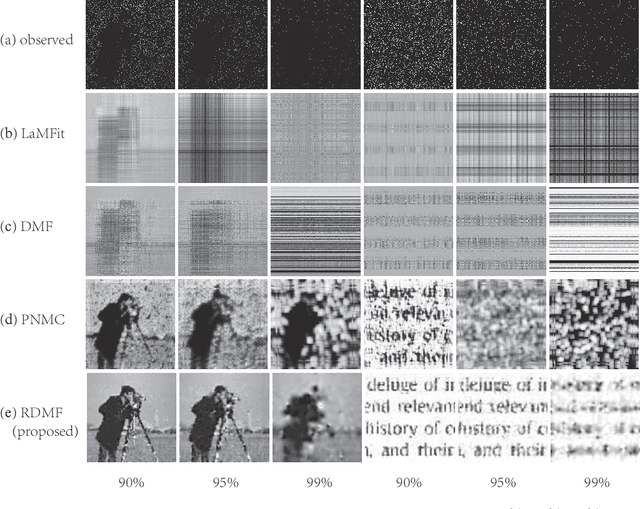
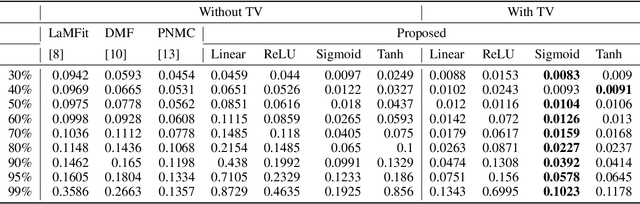
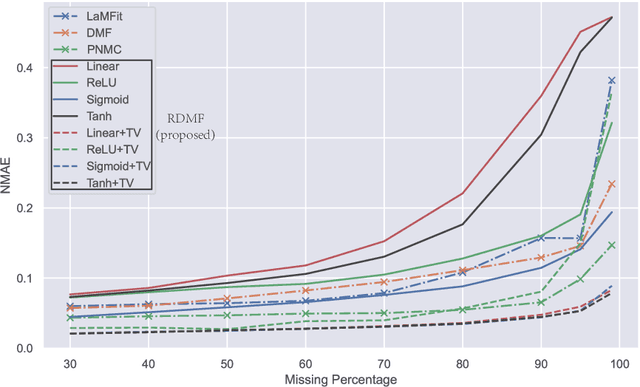
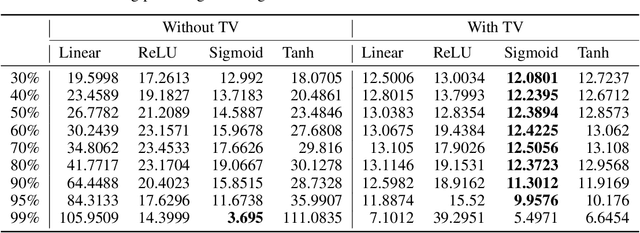
It has been an important approach of using matrix completion to perform image restoration. Most previous works on matrix completion focus on the low-rank property by imposing explicit constraints on the recovered matrix, such as the constraint of the nuclear norm or limiting the dimension of the matrix factorization component. Recently, theoretical works suggest that deep linear neural network has an implicit bias towards low rank on matrix completion. However, low rank is not adequate to reflect the intrinsic characteristics of a natural image. Thus, algorithms with only the constraint of low rank are insufficient to perform image restoration well. In this work, we propose a Regularized Deep Matrix Factorized (RDMF) model for image restoration, which utilizes the implicit bias of the low rank of deep neural networks and the explicit bias of total variation. We demonstrate the effectiveness of our RDMF model with extensive experiments, in which our method surpasses the state of art models in common examples, especially for the restoration from very few observations. Our work sheds light on a more general framework for solving other inverse problems by combining the implicit bias of deep learning with explicit regularization.