Xile Zhao
Compressive Imaging Reconstruction via Tensor Decomposed Multi-Resolution Grid Encoding
Jul 10, 2025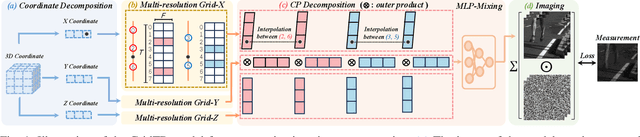

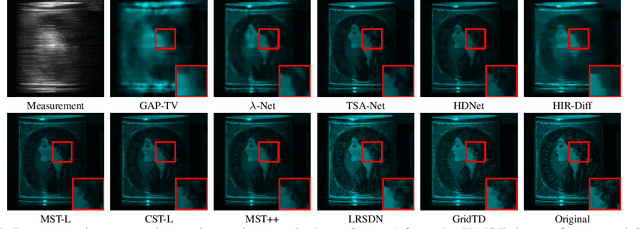
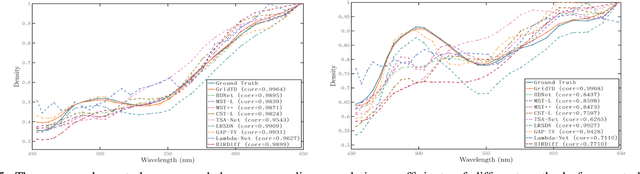
Abstract:Compressive imaging (CI) reconstruction, such as snapshot compressive imaging (SCI) and compressive sensing magnetic resonance imaging (MRI), aims to recover high-dimensional images from low-dimensional compressed measurements. This process critically relies on learning an accurate representation of the underlying high-dimensional image. However, existing unsupervised representations may struggle to achieve a desired balance between representation ability and efficiency. To overcome this limitation, we propose Tensor Decomposed multi-resolution Grid encoding (GridTD), an unsupervised continuous representation framework for CI reconstruction. GridTD optimizes a lightweight neural network and the input tensor decomposition model whose parameters are learned via multi-resolution hash grid encoding. It inherently enjoys the hierarchical modeling ability of multi-resolution grid encoding and the compactness of tensor decomposition, enabling effective and efficient reconstruction of high-dimensional images. Theoretical analyses for the algorithm's Lipschitz property, generalization error bound, and fixed-point convergence reveal the intrinsic superiority of GridTD as compared with existing continuous representation models. Extensive experiments across diverse CI tasks, including video SCI, spectral SCI, and compressive dynamic MRI reconstruction, consistently demonstrate the superiority of GridTD over existing methods, positioning GridTD as a versatile and state-of-the-art CI reconstruction method.
Continuous Representation Methods, Theories, and Applications: An Overview and Perspectives
May 21, 2025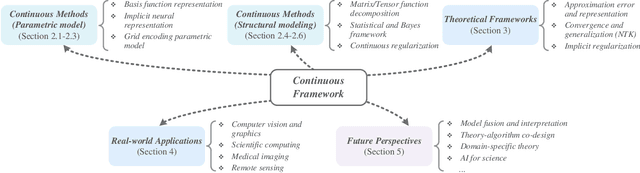
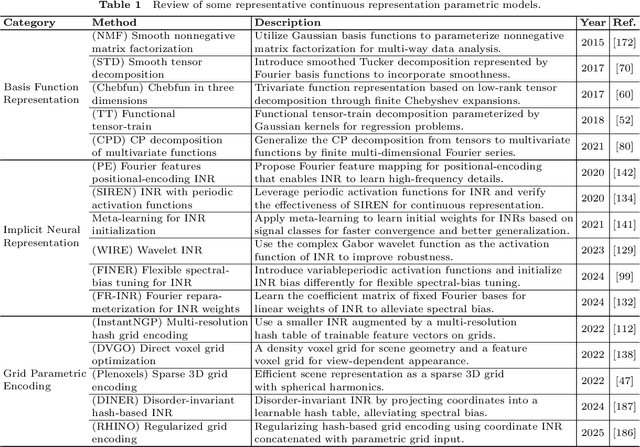
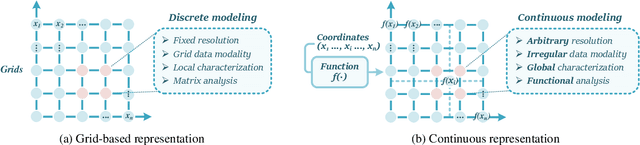
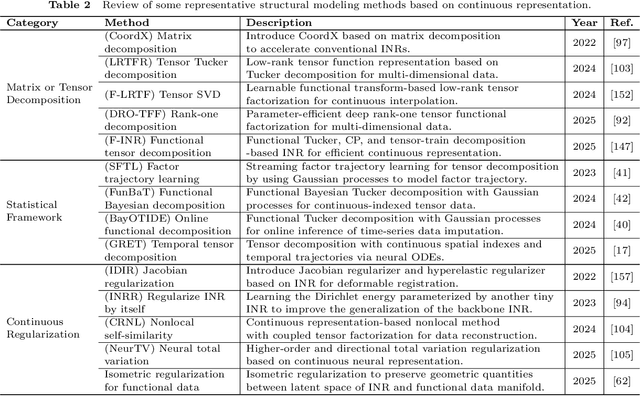
Abstract:Recently, continuous representation methods emerge as novel paradigms that characterize the intrinsic structures of real-world data through function representations that map positional coordinates to their corresponding values in the continuous space. As compared with the traditional discrete framework, the continuous framework demonstrates inherent superiority for data representation and reconstruction (e.g., image restoration, novel view synthesis, and waveform inversion) by offering inherent advantages including resolution flexibility, cross-modal adaptability, inherent smoothness, and parameter efficiency. In this review, we systematically examine recent advancements in continuous representation frameworks, focusing on three aspects: (i) Continuous representation method designs such as basis function representation, statistical modeling, tensor function decomposition, and implicit neural representation; (ii) Theoretical foundations of continuous representations such as approximation error analysis, convergence property, and implicit regularization; (iii) Real-world applications of continuous representations derived from computer vision, graphics, bioinformatics, and remote sensing. Furthermore, we outline future directions and perspectives to inspire exploration and deepen insights to facilitate continuous representation methods, theories, and applications. All referenced works are summarized in our open-source repository: https://github.com/YisiLuo/Continuous-Representation-Zoo.
Cross-Frequency Implicit Neural Representation with Self-Evolving Parameters
Apr 15, 2025Abstract:Implicit neural representation (INR) has emerged as a powerful paradigm for visual data representation. However, classical INR methods represent data in the original space mixed with different frequency components, and several feature encoding parameters (e.g., the frequency parameter $\omega$ or the rank $R$) need manual configurations. In this work, we propose a self-evolving cross-frequency INR using the Haar wavelet transform (termed CF-INR), which decouples data into four frequency components and employs INRs in the wavelet space. CF-INR allows the characterization of different frequency components separately, thus enabling higher accuracy for data representation. To more precisely characterize cross-frequency components, we propose a cross-frequency tensor decomposition paradigm for CF-INR with self-evolving parameters, which automatically updates the rank parameter $R$ and the frequency parameter $\omega$ for each frequency component through self-evolving optimization. This self-evolution paradigm eliminates the laborious manual tuning of these parameters, and learns a customized cross-frequency feature encoding configuration for each dataset. We evaluate CF-INR on a variety of visual data representation and recovery tasks, including image regression, inpainting, denoising, and cloud removal. Extensive experiments demonstrate that CF-INR outperforms state-of-the-art methods in each case.
Superpixel-informed Implicit Neural Representation for Multi-Dimensional Data
Nov 18, 2024Abstract:Recently, implicit neural representations (INRs) have attracted increasing attention for multi-dimensional data recovery. However, INRs simply map coordinates via a multi-layer perception (MLP) to corresponding values, ignoring the inherent semantic information of the data. To leverage semantic priors from the data, we propose a novel Superpixel-informed INR (S-INR). Specifically, we suggest utilizing generalized superpixel instead of pixel as an alternative basic unit of INR for multi-dimensional data (e.g., images and weather data). The coordinates of generalized superpixels are first fed into exclusive attention-based MLPs, and then the intermediate results interact with a shared dictionary matrix. The elaborately designed modules in S-INR allow us to ingenuously exploit the semantic information within and across generalized superpixels. Extensive experiments on various applications validate the effectiveness and efficacy of our S-INR compared to state-of-the-art INR methods.
NeurTV: Total Variation on the Neural Domain
May 27, 2024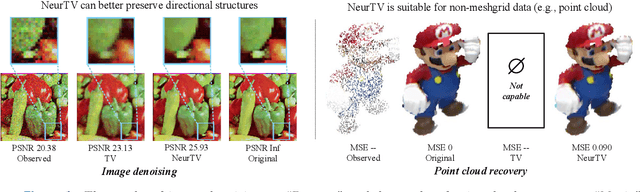
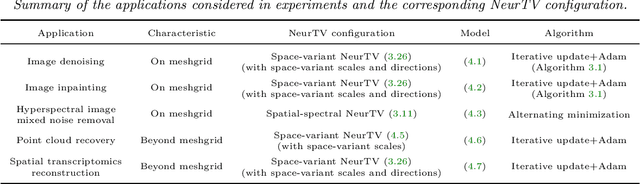

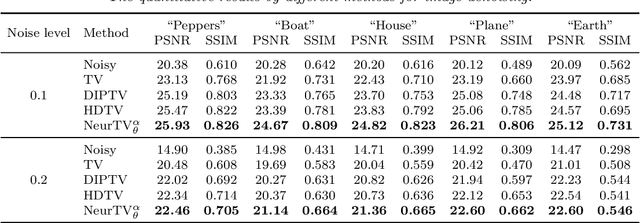
Abstract:Recently, we have witnessed the success of total variation (TV) for many imaging applications. However, traditional TV is defined on the original pixel domain, which limits its potential. In this work, we suggest a new TV regularization defined on the neural domain. Concretely, the discrete data is continuously and implicitly represented by a deep neural network (DNN), and we use the derivatives of DNN outputs w.r.t. input coordinates to capture local correlations of data. As compared with classical TV on the original domain, the proposed TV on the neural domain (termed NeurTV) enjoys two advantages. First, NeurTV is not limited to meshgrid but is suitable for both meshgrid and non-meshgrid data. Second, NeurTV can more exactly capture local correlations across data for any direction and any order of derivatives attributed to the implicit and continuous nature of neural domain. We theoretically reinterpret NeurTV under the variational approximation framework, which allows us to build the connection between classical TV and NeurTV and inspires us to develop variants (e.g., NeurTV with arbitrary resolution and space-variant NeurTV). Extensive numerical experiments with meshgrid data (e.g., color and hyperspectral images) and non-meshgrid data (e.g., point clouds and spatial transcriptomics) showcase the effectiveness of the proposed methods.
Revisiting Nonlocal Self-Similarity from Continuous Representation
Jan 01, 2024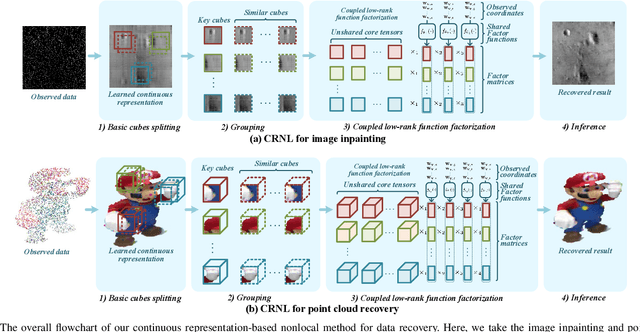
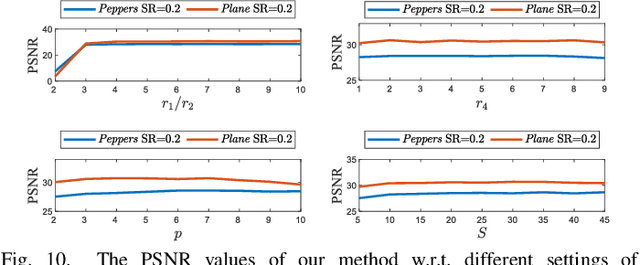
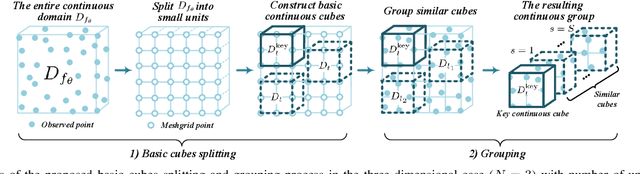

Abstract:Nonlocal self-similarity (NSS) is an important prior that has been successfully applied in multi-dimensional data processing tasks, e.g., image and video recovery. However, existing NSS-based methods are solely suitable for meshgrid data such as images and videos, but are not suitable for emerging off-meshgrid data, e.g., point cloud and climate data. In this work, we revisit the NSS from the continuous representation perspective and propose a novel Continuous Representation-based NonLocal method (termed as CRNL), which has two innovative features as compared with classical nonlocal methods. First, based on the continuous representation, our CRNL unifies the measure of self-similarity for on-meshgrid and off-meshgrid data and thus is naturally suitable for both of them. Second, the nonlocal continuous groups can be more compactly and efficiently represented by the coupled low-rank function factorization, which simultaneously exploits the similarity within each group and across different groups, while classical nonlocal methods neglect the similarity across groups. This elaborately designed coupled mechanism allows our method to enjoy favorable performance over conventional NSS methods in terms of both effectiveness and efficiency. Extensive multi-dimensional data processing experiments on-meshgrid (e.g., image inpainting and image denoising) and off-meshgrid (e.g., climate data prediction and point cloud recovery) validate the versatility, effectiveness, and efficiency of our CRNL as compared with state-of-the-art methods.
An inexact proximal majorization-minimization Algorithm for remote sensing image stripe noise removal
Aug 17, 2023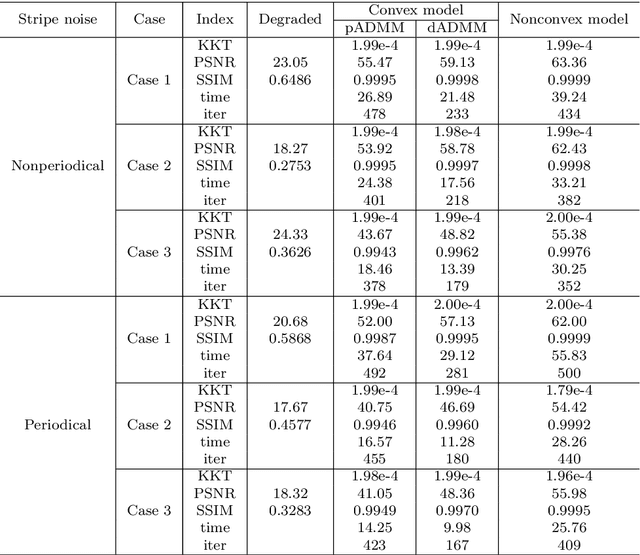



Abstract:The stripe noise existing in remote sensing images badly degrades the visual quality and restricts the precision of data analysis. Therefore, many destriping models have been proposed in recent years. In contrast to these existing models, in this paper, we propose a nonconvex model with a DC function (i.e., the difference of convex functions) structure to remove the strip noise. To solve this model, we make use of the DC structure and apply an inexact proximal majorization-minimization algorithm with each inner subproblem solved by the alternating direction method of multipliers. It deserves mentioning that we design an implementable stopping criterion for the inner subproblem, while the convergence can still be guaranteed. Numerical experiments demonstrate the superiority of the proposed model and algorithm.
H2TF for Hyperspectral Image Denoising: Where Hierarchical Nonlinear Transform Meets Hierarchical Matrix Factorization
Apr 21, 2023Abstract:Recently, tensor singular value decomposition (t-SVD) has emerged as a promising tool for hyperspectral image (HSI) processing. In the t-SVD, there are two key building blocks: (i) the low-rank enhanced transform and (ii) the accompanying low-rank characterization of transformed frontal slices. Previous t-SVD methods mainly focus on the developments of (i), while neglecting the other important aspect, i.e., the exact characterization of transformed frontal slices. In this letter, we exploit the potentiality in both building blocks by leveraging the \underline{\bf H}ierarchical nonlinear transform and the \underline{\bf H}ierarchical matrix factorization to establish a new \underline{\bf T}ensor \underline{\bf F}actorization (termed as H2TF). Compared to shallow counter partners, e.g., low-rank matrix factorization or its convex surrogates, H2TF can better capture complex structures of transformed frontal slices due to its hierarchical modeling abilities. We then suggest the H2TF-based HSI denoising model and develop an alternating direction method of multipliers-based algorithm to address the resultant model. Extensive experiments validate the superiority of our method over state-of-the-art HSI denoising methods.
Low-Rank Tensor Function Representation for Multi-Dimensional Data Recovery
Dec 01, 2022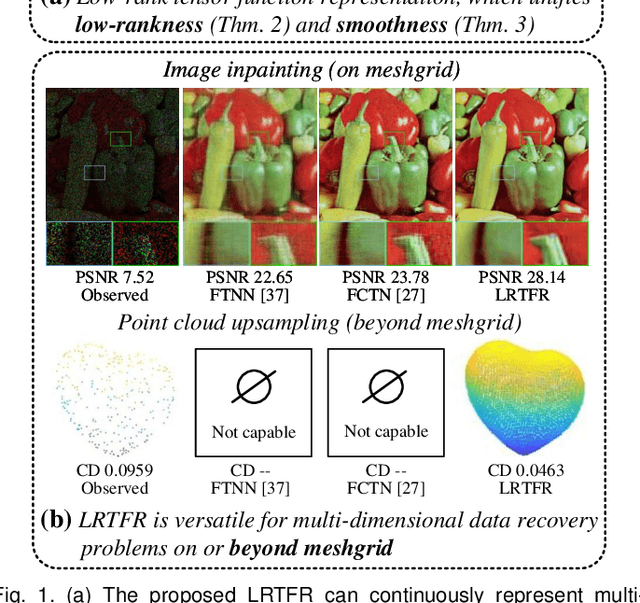
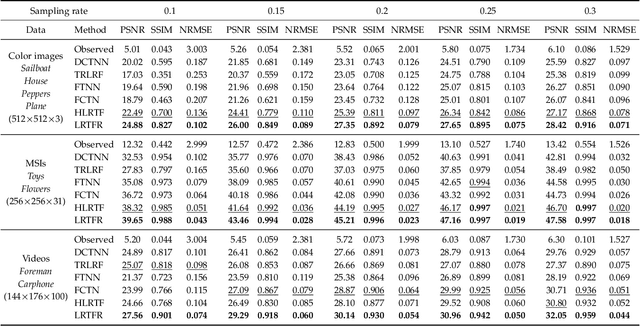
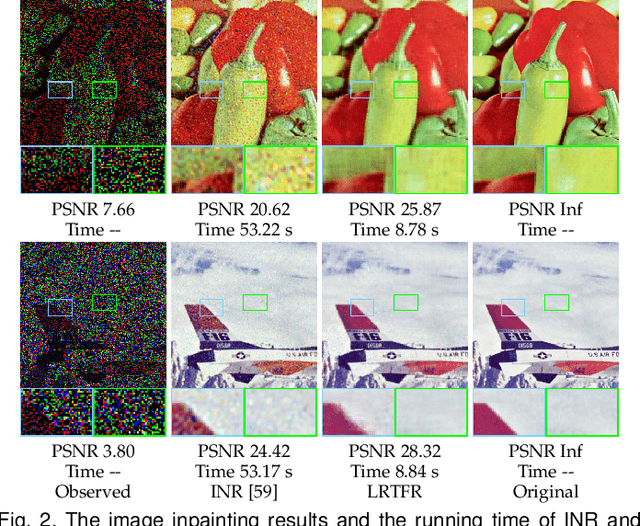
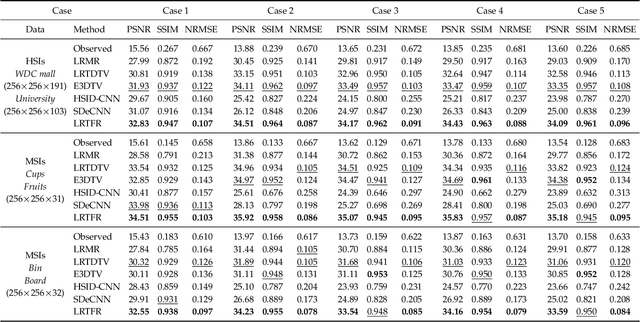
Abstract:Since higher-order tensors are naturally suitable for representing multi-dimensional data in real-world, e.g., color images and videos, low-rank tensor representation has become one of the emerging areas in machine learning and computer vision. However, classical low-rank tensor representations can only represent data on finite meshgrid due to their intrinsical discrete nature, which hinders their potential applicability in many scenarios beyond meshgrid. To break this barrier, we propose a low-rank tensor function representation (LRTFR), which can continuously represent data beyond meshgrid with infinite resolution. Specifically, the suggested tensor function, which maps an arbitrary coordinate to the corresponding value, can continuously represent data in an infinite real space. Parallel to discrete tensors, we develop two fundamental concepts for tensor functions, i.e., the tensor function rank and low-rank tensor function factorization. We theoretically justify that both low-rank and smooth regularizations are harmoniously unified in the LRTFR, which leads to high effectiveness and efficiency for data continuous representation. Extensive multi-dimensional data recovery applications arising from image processing (image inpainting and denoising), machine learning (hyperparameter optimization), and computer graphics (point cloud upsampling) substantiate the superiority and versatility of our method as compared with state-of-the-art methods. Especially, the experiments beyond the original meshgrid resolution (hyperparameter optimization) or even beyond meshgrid (point cloud upsampling) validate the favorable performances of our method for continuous representation.
Unsupervised Deraining: Where Asymmetric Contrastive Learning Meets Self-similarity
Nov 02, 2022
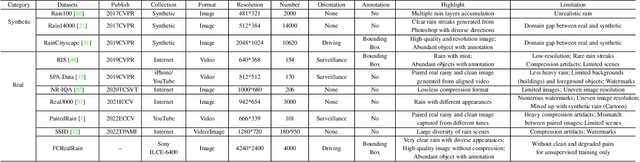

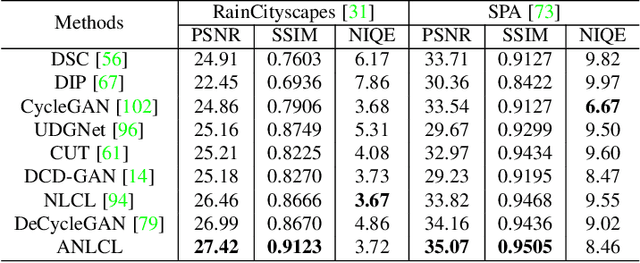
Abstract:Most of the existing learning-based deraining methods are supervisedly trained on synthetic rainy-clean pairs. The domain gap between the synthetic and real rain makes them less generalized to complex real rainy scenes. Moreover, the existing methods mainly utilize the property of the image or rain layers independently, while few of them have considered their mutually exclusive relationship. To solve above dilemma, we explore the intrinsic intra-similarity within each layer and inter-exclusiveness between two layers and propose an unsupervised non-local contrastive learning (NLCL) deraining method. The non-local self-similarity image patches as the positives are tightly pulled together, rain patches as the negatives are remarkably pushed away, and vice versa. On one hand, the intrinsic self-similarity knowledge within positive/negative samples of each layer benefits us to discover more compact representation; on the other hand, the mutually exclusive property between the two layers enriches the discriminative decomposition. Thus, the internal self-similarity within each layer (similarity) and the external exclusive relationship of the two layers (dissimilarity) serving as a generic image prior jointly facilitate us to unsupervisedly differentiate the rain from clean image. We further discover that the intrinsic dimension of the non-local image patches is generally higher than that of the rain patches. This motivates us to design an asymmetric contrastive loss to precisely model the compactness discrepancy of the two layers for better discriminative decomposition. In addition, considering that the existing real rain datasets are of low quality, either small scale or downloaded from the internet, we collect a real large-scale dataset under various rainy kinds of weather that contains high-resolution rainy images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge