An inexact proximal majorization-minimization Algorithm for remote sensing image stripe noise removal

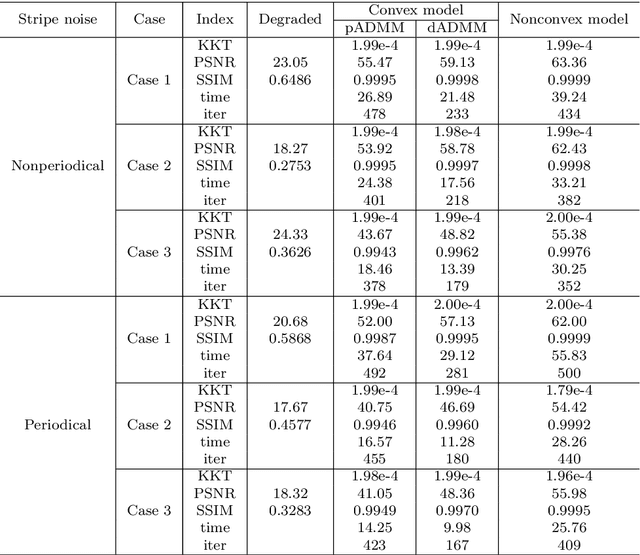
The stripe noise existing in remote sensing images badly degrades the visual quality and restricts the precision of data analysis. Therefore, many destriping models have been proposed in recent years. In contrast to these existing models, in this paper, we propose a nonconvex model with a DC function (i.e., the difference of convex functions) structure to remove the strip noise. To solve this model, we make use of the DC structure and apply an inexact proximal majorization-minimization algorithm with each inner subproblem solved by the alternating direction method of multipliers. It deserves mentioning that we design an implementable stopping criterion for the inner subproblem, while the convergence can still be guaranteed. Numerical experiments demonstrate the superiority of the proposed model and algorithm.

Learning the hub graphical Lasso model with the structured sparsity via an efficient algorithm

Graphical models have exhibited their performance in numerous tasks ranging from biological analysis to recommender systems. However, graphical models with hub nodes are computationally difficult to fit, particularly when the dimension of the data is large. To efficiently estimate the hub graphical models, we introduce a two-phase algorithm. The proposed algorithm first generates a good initial point via a dual alternating direction method of multipliers (ADMM), and then warm starts a semismooth Newton (SSN) based augmented Lagrangian method (ALM) to compute a solution that is accurate enough for practical tasks. The sparsity structure of the generalized Jacobian ensures that the algorithm can obtain a nice solution very efficiently. Comprehensive experiments on both synthetic data and real data show that it obviously outperforms the existing state-of-the-art algorithms. In particular, in some high dimensional tasks, it can save more than 70\% of the execution time, meanwhile still achieves a high-quality estimation.

An efficient algorithm for the $\ell_{p}$ norm based metric nearness problem

Given a dissimilarity matrix, the metric nearness problem is to find the nearest matrix of distances that satisfy the triangle inequalities. This problem has wide applications, such as sensor networks, image processing, and so on. But it is of great challenge even to obtain a moderately accurate solution due to the $O(n^{3})$ metric constraints and the nonsmooth objective function which is usually a weighted $\ell_{p}$ norm based distance. In this paper, we propose a delayed constraint generation method with each subproblem solved by the semismooth Newton based proximal augmented Lagrangian method (PALM) for the metric nearness problem. Due to the high memory requirement for the storage of the matrix related to the metric constraints, we take advantage of the special structure of the matrix and do not need to store the corresponding constraint matrix. A pleasing aspect of our algorithm is that we can solve these problems involving up to $10^{8}$ variables and $10^{13}$ constraints. Numerical experiments demonstrate the efficiency of our algorithm. In theory, firstly, under a mild condition, we establish a primal-dual error bound condition which is very essential for the analysis of local convergence rate of PALM. Secondly, we prove the equivalence between the dual nondegeneracy condition and nonsingularity of the generalized Jacobian for the inner subproblem of PALM. Thirdly, when $q(\cdot)=\|\cdot\|_{1}$ or $\|\cdot\|_{\infty}$, without the strict complementarity condition, we also prove the equivalence between the the dual nondegeneracy condition and the uniqueness of the primal solution.

A dual semismooth Newton based augmented Lagrangian method for large-scale linearly constrained sparse group square-root Lasso problems

Square-root Lasso problems are proven robust regression problems. Furthermore, square-root regression problems with structured sparsity also plays an important role in statistics and machine learning. In this paper, we focus on the numerical computation of large-scale linearly constrained sparse group square-root Lasso problems. In order to overcome the difficulty that there are two nonsmooth terms in the objective function, we propose a dual semismooth Newton (SSN) based augmented Lagrangian method (ALM) for it. That is, we apply the ALM to the dual problem with the subproblem solved by the SSN method. To apply the SSN method, the positive definiteness of the generalized Jacobian is very important. Hence we characterize the equivalence of its positive definiteness and the constraint nondegeneracy condition of the corresponding primal problem. In numerical implementation, we fully employ the second order sparsity so that the Newton direction can be efficiently obtained. Numerical experiments demonstrate the efficiency of the proposed algorithm.

A proximal-proximal majorization-minimization algorithm for nonconvex tuning-free robust regression problems

In this paper, we introduce a proximal-proximal majorization-minimization (PPMM) algorithm for nonconvex tuning-free robust regression problems. The basic idea is to apply the proximal majorization-minimization algorithm to solve the nonconvex problem with the inner subproblems solved by a sparse semismooth Newton (SSN) method based proximal point algorithm (PPA). We must emphasize that the main difficulty in the design of the algorithm lies in how to overcome the singular difficulty of the inner subproblem. Furthermore, we also prove that the PPMM algorithm converges to a d-stationary point. Due to the Kurdyka-Lojasiewicz (KL) property of the problem, we present the convergence rate of the PPMM algorithm. Numerical experiments demonstrate that our proposed algorithm outperforms the existing state-of-the-art algorithms.

A sparse semismooth Newton based augmented Lagrangian method for large-scale support vector machines

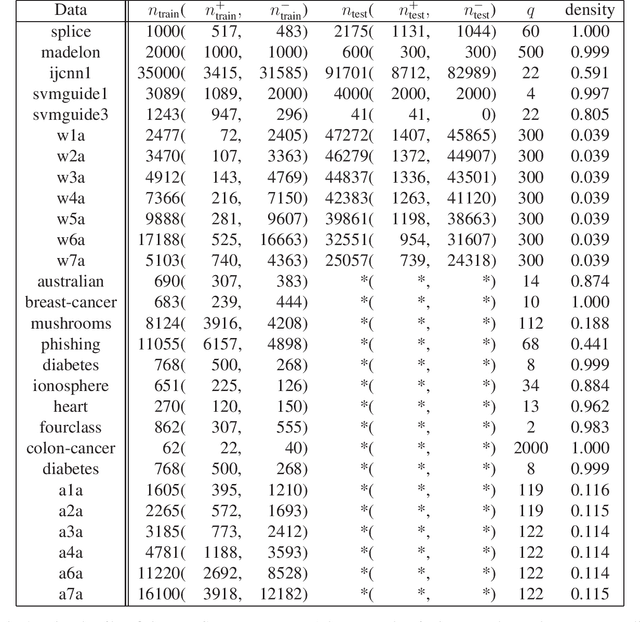
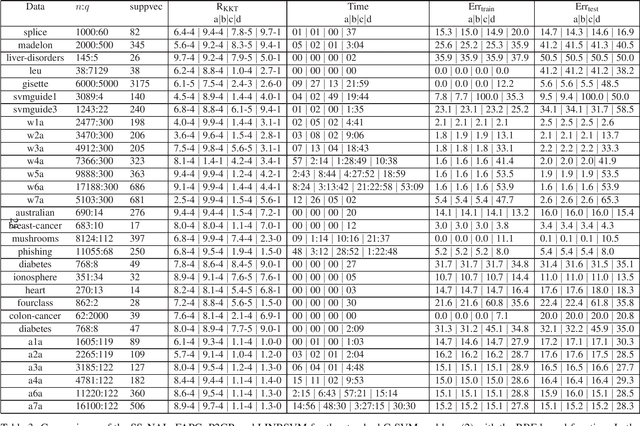
Support vector machines (SVMs) are successful modeling and prediction tools with a variety of applications. Previous work has demonstrated the superiority of the SVMs in dealing with the high dimensional, low sample size problems. However, the numerical difficulties of the SVMs will become severe with the increase of the sample size. Although there exist many solvers for the SVMs, only few of them are designed by exploiting the special structures of the SVMs. In this paper, we propose a highly efficient sparse semismooth Newton based augmented Lagrangian method for solving a large-scale convex quadratic programming problem with a linear equality constraint and a simple box constraint, which is generated from the dual problems of the SVMs. By leveraging the primal-dual error bound result, the fast local convergence rate of the augmented Lagrangian method can be guaranteed. Furthermore, by exploiting the second-order sparsity of the problem when using the semismooth Newton method, the algorithm can efficiently solve the aforementioned difficult problems. Finally, numerical comparisons demonstrate that the proposed algorithm outperforms the current state-of-the-art solvers for the large-scale SVMs.

A sparse semismooth Newton based proximal majorization-minimization algorithm for nonconvex square-root-loss regression problems

In this paper, we consider high-dimensional nonconvex square-root-loss regression problems and introduce a proximal majorization-minimization (PMM) algorithm for these problems. Our key idea for making the proposed PMM to be efficient is to develop a sparse semismooth Newton method to solve the corresponding subproblems. By using the Kurdyka-{\L}ojasiewicz property exhibited in the underlining problems, we prove that the PMM algorithm converges to a d-stationary point. We also analyze the oracle property of the initial subproblem used in our algorithm. Extensive numerical experiments are presented to demonstrate the high efficiency of the proposed PMM algorithm.

A Dual Symmetric Gauss-Seidel Alternating Direction Method of Multipliers for Hyperspectral Sparse Unmixing

Since sparse unmixing has emerged as a promising approach to hyperspectral unmixing, some spatial-contextual information in the hyperspectral images has been exploited to improve the performance of the unmixing recently. The total variation (TV) has been widely used to promote the spatial homogeneity as well as the smoothness between adjacent pixels. However, the computation task for hyperspectral sparse unmixing with a TV regularization term is heavy. Besides, the convergences of the traditional sparse unmixing algorithms which are special cases of the primal alternating direction method of multipliers (pADMM) have not been explained in details. In this paper, we design an efficient and convergent dual symmetric Gauss-Seidel ADMM (sGS-ADMM) for hyperspectral sparse unmixing with a TV regularization term. We also present the global convergence and local linear convergence rate analysis for the traditional sparse unmixing algorithm and our algorithm. As demonstrated in numerical experiments, our algorithm can obviously improve the efficiency of the unmixing compared with the state-of-the-art algorithm. More importantly, we can obtain images with higher quality.